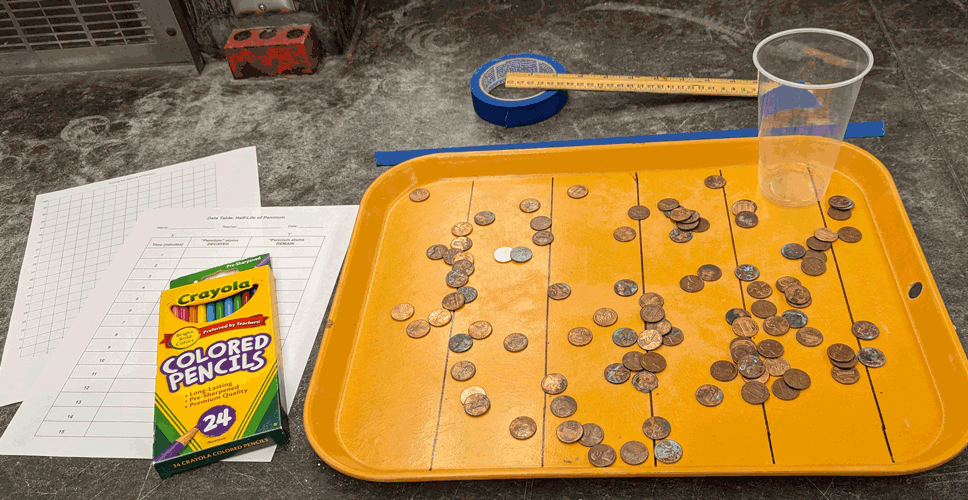What is Half-life?
Lesson Overview
In this lesson, students will simulate the randomness of decay in radioactive atoms and visualize the half-life of a sample radioactive element.
Timing
This lesson can be completed in two (2) 45-minute class periods. One class period should be used for performing the activity. In the second class period, students will analyze the data and answer the discussion questions.
Learning Objectives
- Students will model the randomness of decay in a fictional radioactive element (Pennium).
- Students will learn how to calculate the half-life of a radioactive element.
Teachers: Request an Answer Key
Connections to Content Standards, Crosscutting Concepts, Science and Engineering Practices
Materials
- Ruler
- 100 “Pennium” atoms
- Masking tape
- Cup
- Tray marked with lines (3-inches apart)
- Colored pencils
- Data Table: The Half-Life of Pennium
- Graph Paper: The Half-Life of Pennium
- Student Handout: Procedure and Data Analysis
- Student Handout: Discussion Questions
Procedure
- Wear safety glasses! Place a 12-inch piece of masking tape at the front of your desk.
- Get a bag of 100 “Pennium” atoms and a tray that has lines on the bottom, marked 3-inches apart.
- Sprinkle the “Pennium” atoms (randomly) on the tray. Try to keep the pennies from stacking on top of one another.
- “Pennium” atoms that touch the lines are decayed. Remove and count the decayed atoms.
- The number of decayed atoms that you count will be the number of atoms that decayed in 1 minute. Record this number in the data table.
- Place the decayed atoms in one stack at the far left of the masking tape. They will not be used again.
- Subtract the number of decayed atoms in your first stack from 100. Record the difference in your data table as the number of atoms that REMAIN (after the decayed atoms are removed). This is the number of “Pennium” atoms LEFT after 1 minute.
- Gather the remaining “Pennium” atoms (all the atoms not in the first stack) and place them back in the cup. Sprinkle them (randomly) on the tray.
- Remove and count the decayed atoms (any that are touching a line).
- Record this number in the data table (as the number decayed after 2 minutes).
- Place the decayed atoms in a second stack, to the right of the first stack you made (Step 6).
- Calculate the number of remaining atoms by subtracting the number of pennies in Stack 2 from the number of pennies REMAINING after 1 minute. Record this number on your data table as remaining atoms after 2 minutes.
- Continue to sprinkle, count, record, and stack until only 0 or 1 penny remains.
Data Analysis
- Get a sheet of graph paper.
- Label the y-axis: Remaining Atoms. Label the x-axis: Time (minutes)
- Plot the points from the data table as an ordered pair (x,y).
- The ‘x’ is equal to the minute value.
- The ‘y’ is equal to the number of remaining atoms for each minute.
- EXAMPLE: The FIRST point would be (0,100). Time = 0 minutes and all 100 “Pennium” atoms still remain.
- Draw a smooth, best-fit CURVE through the data points.
- Find the point on the y-axis where the remaining “Pennium” atoms is exactly one-half of the atoms at Time = 0 minutes. (HINT: What is half of 100?)
- Starting at the one-half value on the y-axis, draw a line parallel to the x-axis until the line reaches the best-fit curve.
- When the parallel line reaches the curve, draw a vertical line DOWN to the x-axis.
- The point where the vertical line touches the x-axis is the half-life of “Pennium” in minutes.
Discussion
- With each trial (minute), were there more or fewer Pennium atoms that decayed?
- Does your answer to Question 1 indicate that the Pennium atoms are becoming more stable or less stable with each trial (minute)?
- What is the half-life of Pennium? (Be sure to label the answer with the appropriate units.)
- Was it possible to tell which Pennium atoms were going to decay (touch a line) BEFORE they were sprinkled on the box top? Explain.
- Using the half-life value recorded in Question 3, how much time would pass before three half-lives of the Pennium atom occurred?
- In a sample of 3,000 Pennium atoms, how many Pennium atoms would remain at the end of three half-lives?
NGSS Standards: What is Half-Life?
(Middle School)
https://www.nextgenscience.org/pe/ms-ps1-3-matter-and-its-interactions
- Although more general, this standard can involve discussions about radioactive materials and their decay, including half-life, in the context of synthetic materials and their applications.
(High School)
https://www.nextgenscience.org/pe/hs-ps1-8-matter-and-its-interactions
- This standard involves understanding nuclear processes, including radioactive decay, which directly relates to the concept of half-life.
https://www.nextgenscience.org/pe/hs-ess1-6-earths-place-universe
- This standard includes the use of radioactive decay and half-life calculations to date geological materials and understand the timeline of Earth's history.
https://www.nextgenscience.org/hs-ess2-3-earths-systems
- While this standard primarily focuses on Earth’s internal processes, understanding radioactive decay and half-life is crucial for explaining the heat generated by radioactive isotopes within Earth’s interior.
These Crosscutting Concepts and Science and Engineering Practices help students understand and apply the concept of half-life within the broader framework of the NGSS, fostering a comprehensive approach to learning about radioactive decay.
Crosscutting Concepts:
- Patterns: Identifying and using patterns to understand and predict the behavior of radioactive decay and half-life. (Example: Observing the consistent pattern of decay in which half of a radioactive sample decays over each half-life period.)
- Cause and Effect: Understanding the cause of radioactive decay and its predictable effect over time. (Example: Exploring how the inherent instability of certain isotopes causes them to decay at a predictable rate, resulting in a calculable half-life.)
- Scale, Proportion, and Quantity: Addressing the mathematical relationships involved in half-life and how they apply to different scales of observation. (Example: Calculating the remaining quantity of a radioactive substance after several half-lives.)
- Systems and System Models: Using models to represent the process of radioactive decay and the concept of half-life within a system. (Example: Developing and using models to simulate the decay process of radioactive isotopes and to visualize the concept of half-life.)
- Stability and Change: Analyzing the stability of radioactive isotopes and how they change over time through decay. (Example: Understanding how a radioactive isotope becomes more stable as it decays and transforms into a different element or isotope.)
Science and Engineering Practices:
- Asking Questions and Defining Problems: Formulating questions about the nature and implications of half-life in various contexts. (Example: Asking questions about how the half-life of a radioactive isotope affects its use in carbon dating.)
- Developing and Using Models: Creating models to describe and predict the decay process and the concept of half-life. (Example: Using a model to simulate the decay of a radioactive substance and to illustrate how half-life is determined.)
- Planning and Carrying Out Investigations: Designing and conducting experiments to measure half-life and observe radioactive decay. (Example: Using simulated or actual radioactive materials to measure their decay rates and determine their half-lives.)
- Analyzing and Interpreting Data: Interpreting data from decay experiments to understand half-life and make predictions about radioactive decay. (Example: Analyzing decay curves and data from experiments to calculate the half-life of a radioactive isotope.)
- Constructing Explanations and Designing Solutions: Developing explanations for the behavior of radioactive isotopes based on their half-lives and designing related solutions. (Example: Explaining the principles behind radiometric dating techniques that use half-life to determine the age of geological materials.)
- Engaging in Argument from Evidence: Using evidence to support claims about the predictability and implications of half-life. (Example: Arguing the reliability of half-life as a tool used in radiometric dating based on experimental data and established decay rates.)
- Obtaining, Evaluating, and Communicating Information: Gathering and presenting information about half-life and its applications in various fields. (Example: Researching the use of isotopes with specific half-lives in radiometric dating.)
This lab was created with support from Dr. Nathaniel Lifton at Purdue University with funding from the National Science Foundation grant AGS-2303294 (P4CLIMATE).