Discussion and hints

Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS
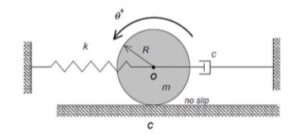
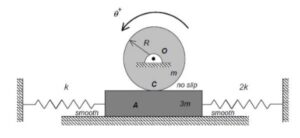
As the system moves, there is no slipping between the contact point C on the drum and block A.  This represents a constraint between the drum rotation and the block translation. We will deal with this in Step 3 of the derivation of the equation of motion below.

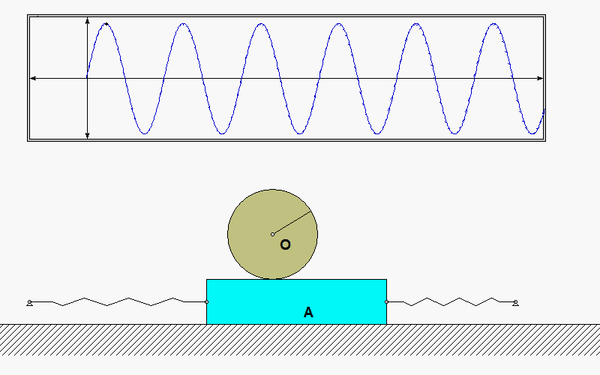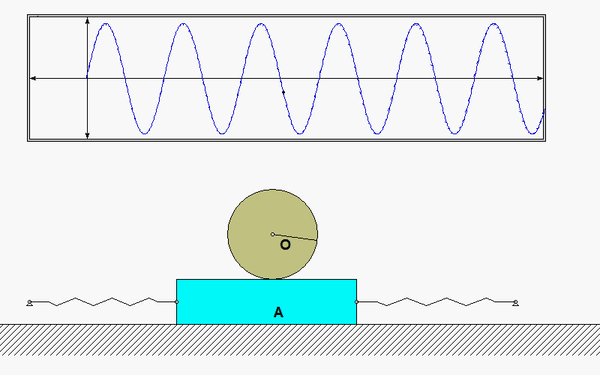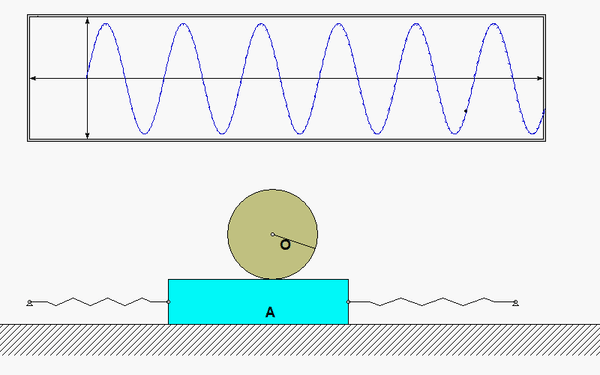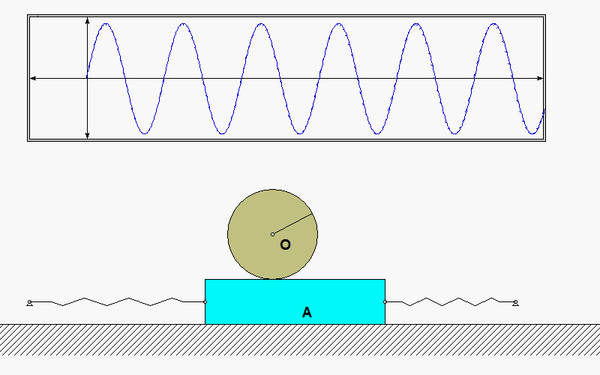
Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw individual free body diagrams (FBDs) of the drum and the disk. Be sure to include the equal-and-opposite contact forces on both the drum and the block. It is important to temporarily define a coordinate that describes the motion of the block. Let's call that variable "x", and define it to be positive to the right. With this definition, the spring forces on the left and right side of the block are kx and 2kx, respectively, with both forces pointing to the left.

Step 2: Kinetics (Newton/Euler)
Using your FBDs from above, write down the Euler equation for the drum, and the Newton equation for the block. Combine these two equations through the elimination of the drum-to-block contact force.

Step 3: Kinematics
You need to relate the angular acceleration of the drum to the acceleration of the block. How is this done? What are the results? Also, how do you relate the stretch/compression x in the two springs in terms of θ?

Step 4: EOM
From your equations in Steps 2 and 3, derive the equation of motion (EOM) of the system in terms of θ.

Once you have determined the EOM for the system, identify the natural frequency from the EOM. Also from the EOM, we know that the general form of the response is: θ(t) = C*cos(ω_nt)+ S*sin(ω_nt). How do you find the response coefficients C and S?

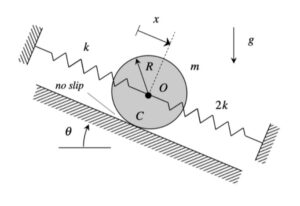
Discussion and hints:

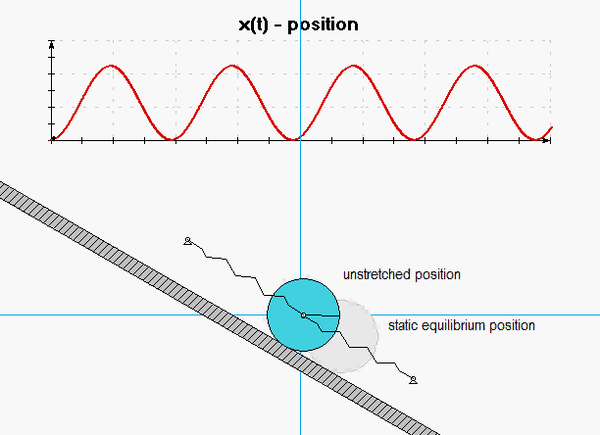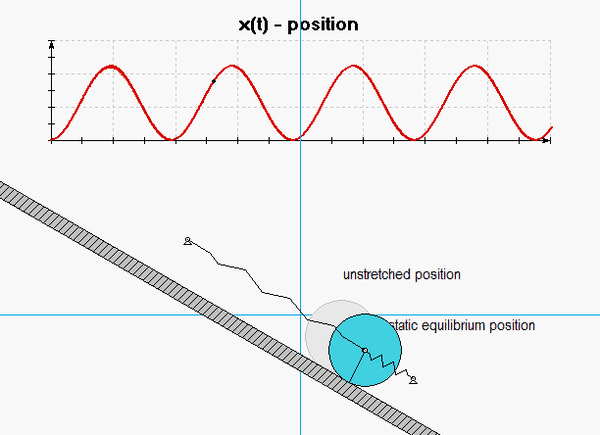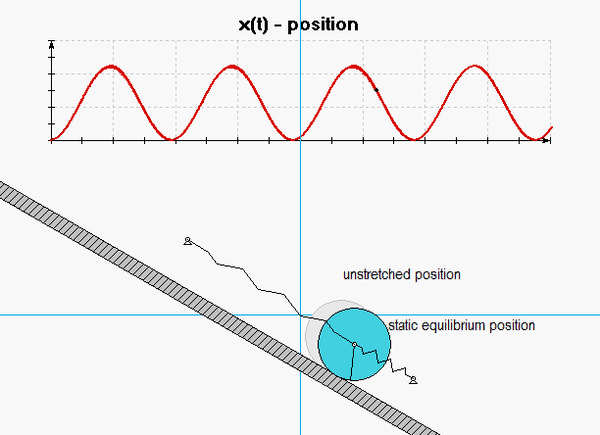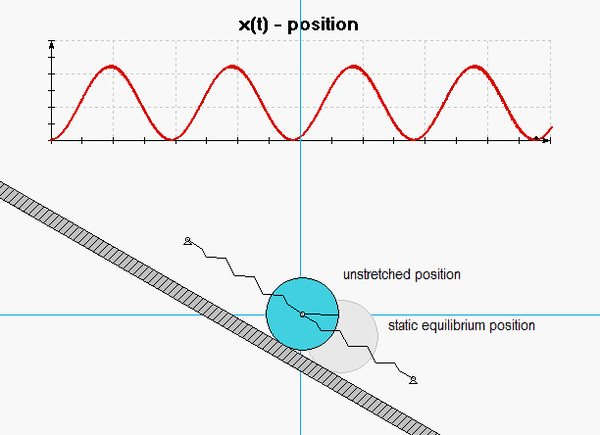
The derivation of the dynamical equation of motion (EOM) for a system is a straight-forward application of what we have learned from Chapter 5 in using the Newton-Euler equations. The goal in deriving the EOM is to end up with a single differential equation in terms of a single dependent variable that describes the motion of the system. Here in this problem, we want our EOM to be in terms of x(t).

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a FBD of the disk. Define a rotation coordinate for the disk.

Step 2: Kinetics (Newton/Euler)
Write down the Newton/Euler equations for the disk.

Step 3: Kinematics
Use the no-slip condition between the disk and the ramp to relate x to the rotational coordinate that you chose above.

Step 4: EOM
Combine your Newton/Euler equations along with your kinematics to arrive at a single differential equation in terms of the dependent variable x.

Any questions?

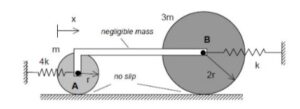
Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link.

Discussion and hints

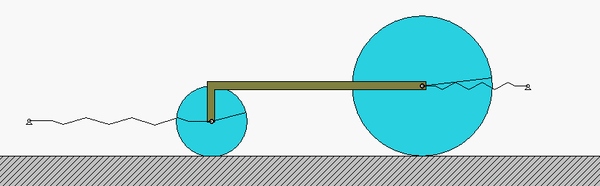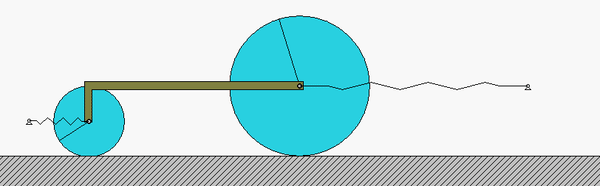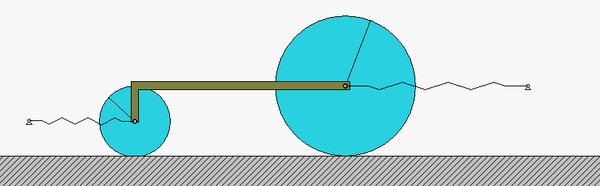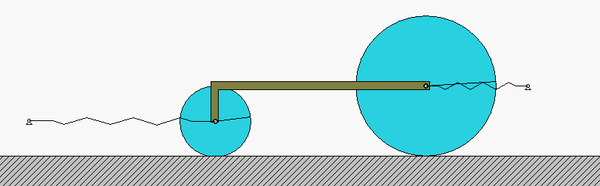
The four-step plan:

1. FBD: It is recommended that you draw individual free body diagrams of each disk and of bar AB. Note that the mass of AB is negligible and that forces are applied at only two points (i.e., a two-force member). What does this say about the direction of the forces on the disks at A and B?
2. Kinetics: Recommended that you use an Euler equation about the contact point of each disk since those are no-slip points for whose accelerations are directed toward the center of mass of each disk. Note that both of these two equations will involve the load carried by AB. You can eliminate that load from these equations, resulting in a single equation.
3. Kinematics: Note that rigid bar AB insures that the velocities of points A and B are the same. How can this be used to relate the angular accelerations of the two disks? Can you see this kinematic relationship between the angular accelerations in the animation above? Please note that the angular accelerations of the two disks are NOT the same, although their centers have the same accelerations.
4. EOM: Combine your results from Steps 2 and 3 to produce a single differential equation of motion (EOM) in terms of the x-coordinate.

Any questions? Ask/answer questions in the discussion thread below.

DISCUSSION

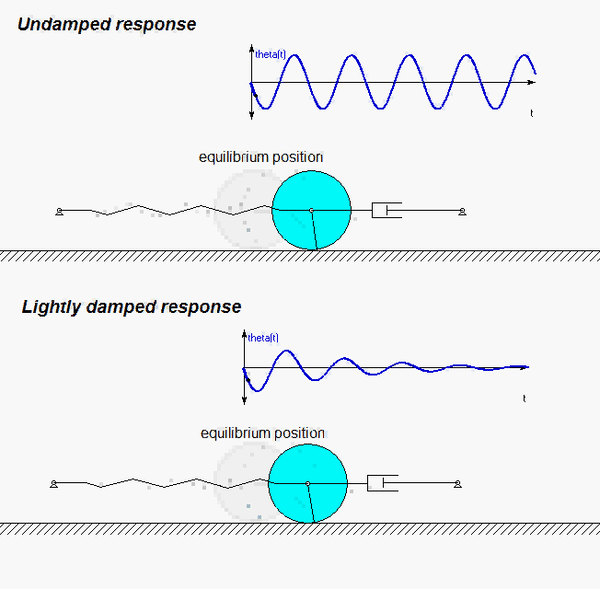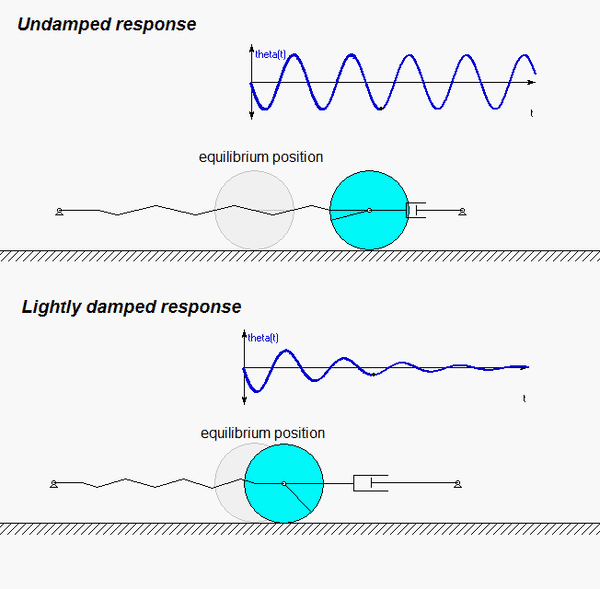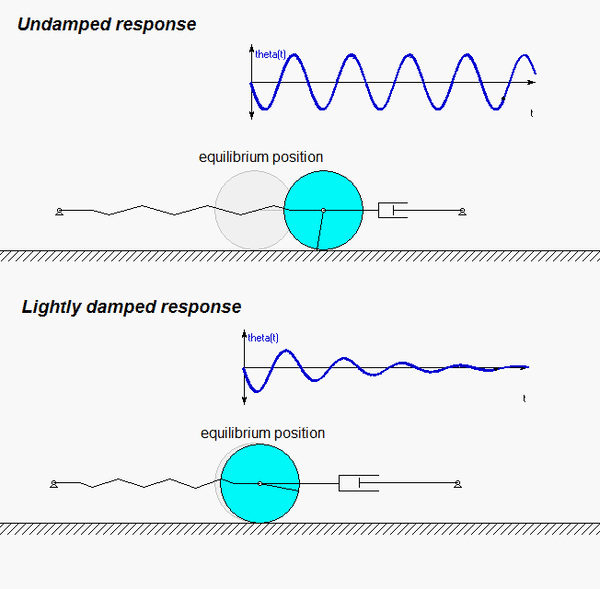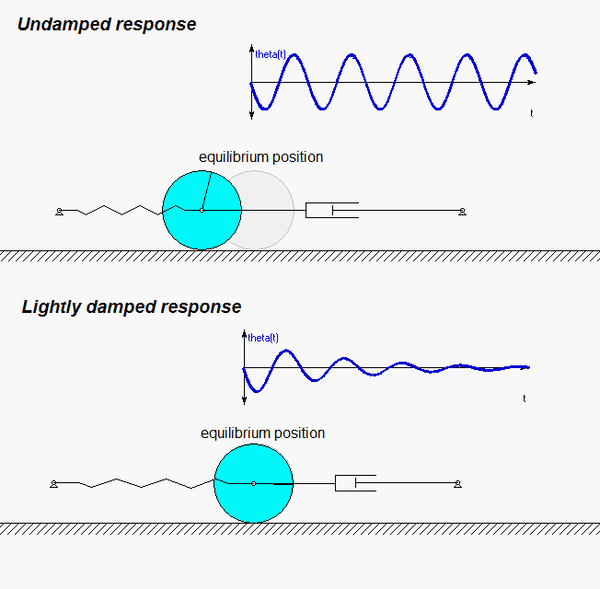
The animation below is for the case of c = 0 (undamped).

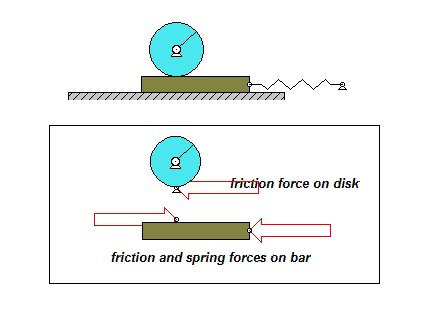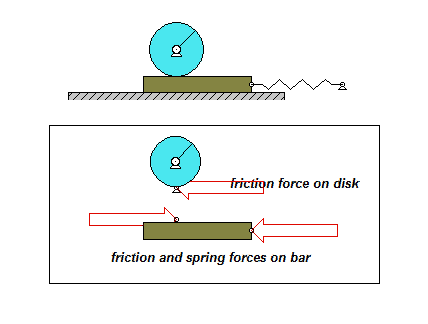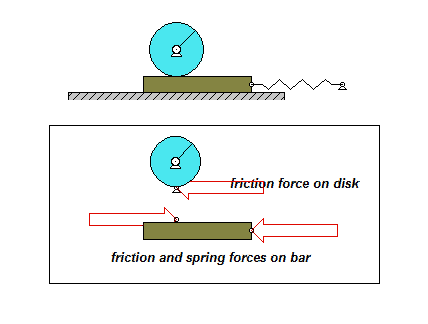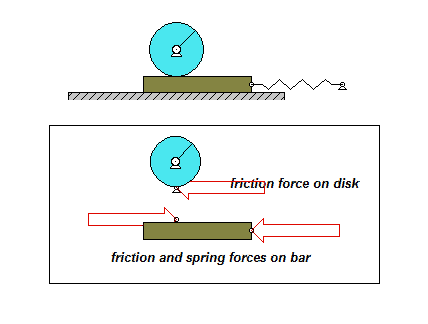
The derivation of the dynamical equation of motion (EOM) for a system is a straight-forward application of what we have learned from Chapter 5 in using the Newton-Euler equations. The goal in deriving the EOM is to end up with a single differential equation in terms of a single dependent variable that describes the motion of the system. Here in this problem, we want our EOM to be in terms of θ(t).

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw individual free body diagrams for the drum and the block. Choose a translational coordinate (say x, defined as being positive to the left).  Be sure the get the correct direction for the spring and dashpot forces on the block. Also, take care in drawing the friction force on the drum as being equal and opposite to the friction force on the block.

Step 2: Kinetics (Newton/Euler)
Write down the Newton/Euler equations for the drum and block based on your FBDs above. Be sure to be in consistent in your sign conventions for forces/translation and moments/rotation.

Step 3: Kinematics
The contact point of the drum on the block (call it point A) is a no-slip point; that is, the horizontal component of acceleration of A is equal to the acceleration of the block.

Step 4: EOM
Combine your Newton/Euler equations along with your kinematics to arrive at a single differential equation in terms of the dependent variable θ.

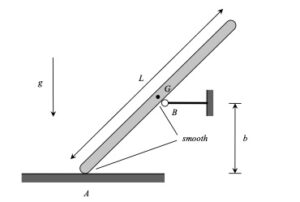
We encourage you to interact with your colleagues here in conversations about this homework problem.

DISCUSSION
As always, we should follow the four-step plan:

STEP 1: FBD
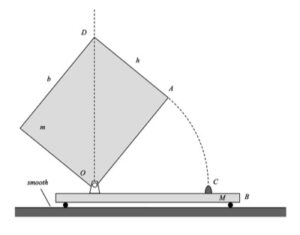
Draw an FBD of the bar. Since the support at B is smooth, the reaction on the bar at B will be perpendicular to the bar.

STEP 2: Kinetics
You should write down the two Newton equations, and the Euler equation. As always, take care in choosing your reference point for Euler's equation. Since we have no fixed points for the bar, you should choose the center of mass G as your reference point.

STEP 3: Kinematics
Note that the path of the center of mass G is tangent to the surface of the bar (that is, the bar can move only along the support, not into the support). With the bar being released from rest, the acceleration of G is tangent to the path. Specifically, the acceleration of G is directed along the direction of the bar. Write down the rigid body kinematics equation that relates the accelerations of A and G. This vector equation represents two scalar equations (x- and y-components).

STEP 4: Solve
At this point, you will have three kinetics equations and two kinematics equations, for a total of five equations. You will have five unknowns. Solve!

Any questions?

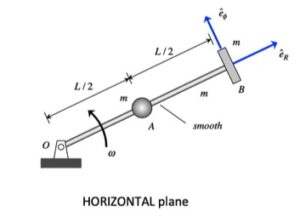
Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.

DISCUSSION

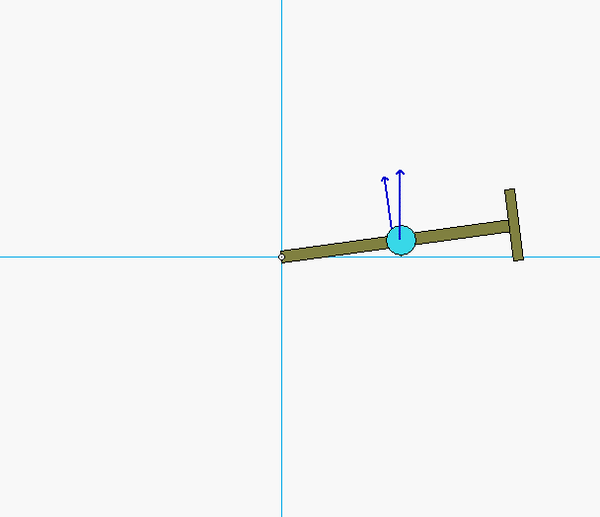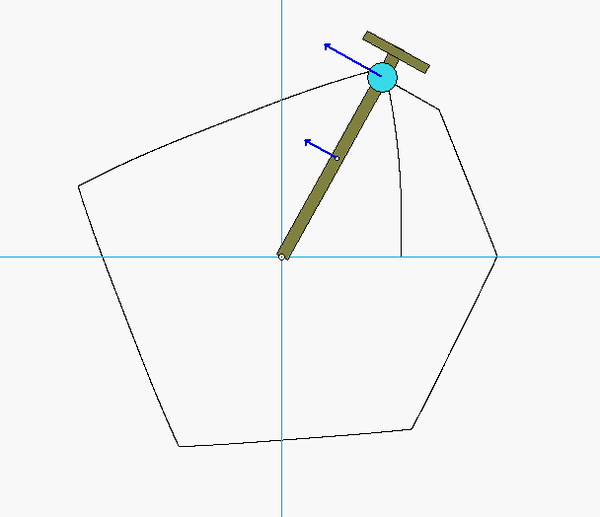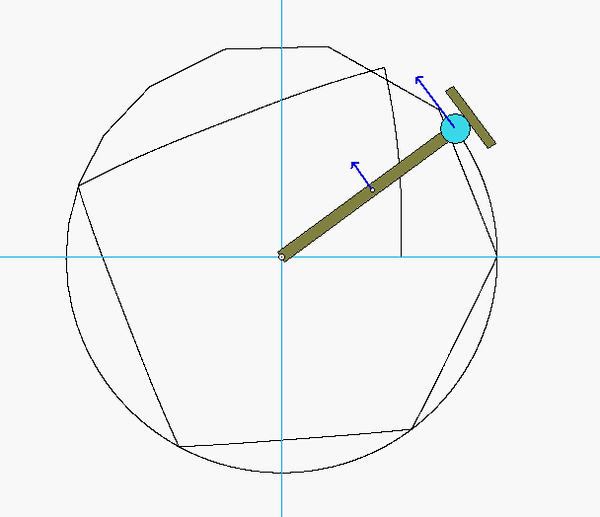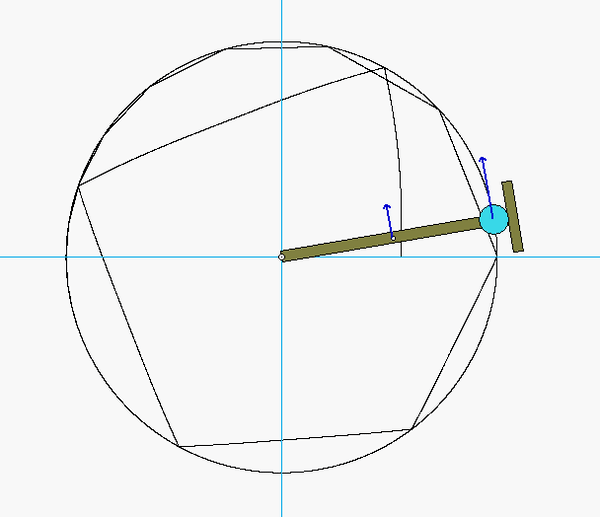
Four-step plan

Step 1: FBD
Draw a free-body diagram particles A and B, along with the bar, altogether. Is angular momentum for this system conserved? Why, or why not?

Step 2: Kinetics - Angular impulse/momentum
Write down the angular momentum for A, B and the bar individually, and then add together. For a particle A, for example, recall that angular momentum is given by H_O = m r_A/O x v_A.  For a rigid body, H_O = I_Oω. You will also need the coefficient of restitution equation relating the radial (normal components here) components of velocity of A and B during impact.

Step 3: Kinematics
For writing down the velocity of points A and B, a polar description is recommended. For example, v_A = R_dot e_R + Rωe_θ.

Step 4: Solve
Solve your equations from Steps 2 and 3 for the velocity of P. Do not forget that A will have both radial and transverse components of velocity.

Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.

Discussion and hints

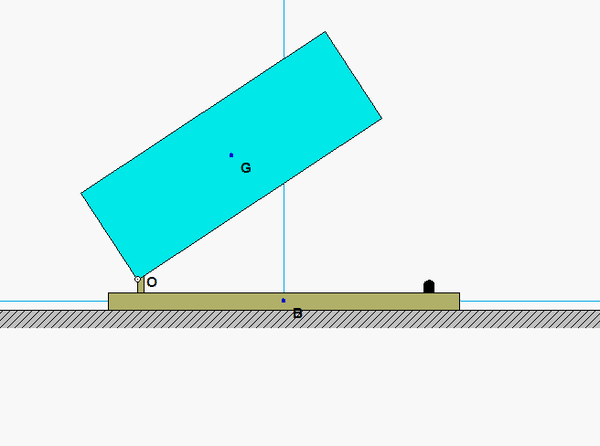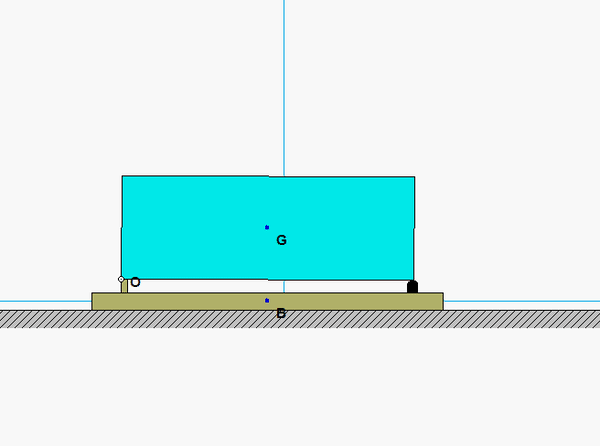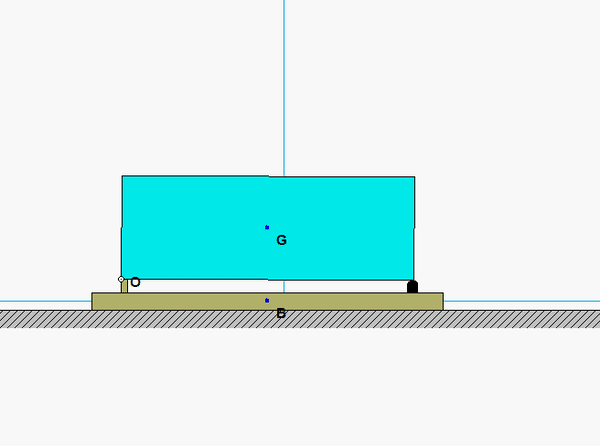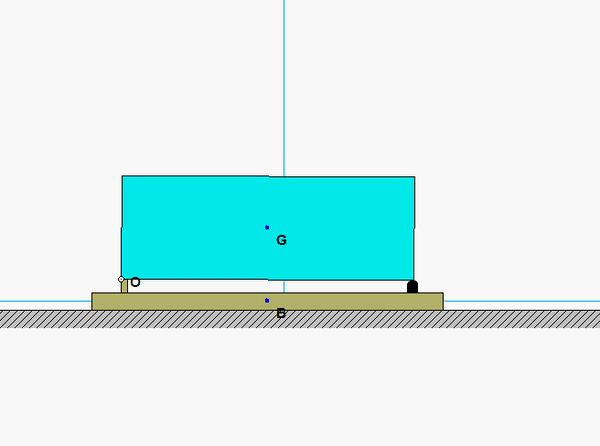
The four-step plan:

1. FBD: It is recommended that you draw a free body diagram of the plate and cart combined.
2. Kinetics: Your FBD should show that the summation of forces in the direction of motion for the cart (call that the x-direction) is zero; therefore, linear momentum in the x-direction is conserved for ALL time. Also note that energy is conserved up to the point of impact. During impact, energy is not conserved; however, you are given the coefficient of restitution (COR) for the impact.
3. Kinematics: Write down the rigid body velocity equation relating the motion of points O and the plate's center of mass G. Here you will use the fact that the cart moves only in the x-direction.
4. Solve

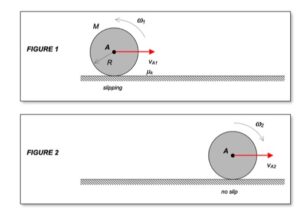
Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.

Discussion

.

The animation shown above demonstrates the relationship between the translation velocity of the disk's center A and the angular velocity of the disk. Recall that the disk is initially projected to the right with an initial velocity of A and a counterclockwise rotation rate; that is, the disk is given a "backspin" on release.

As the disk slides, the friction with the floor does two things: it slows down the translational motion of the disk, and exerts a clockwise moment on the disk reducing the rotational rate of the disk. At some point the rotation rate changes from counterclockwise (positive) to clockwise (negative). And shortly after that, slipping ceases to exist between the disk and the floor. Rolling without slipping starts at the point where the plots of velocity of A and angular velocity of the disk go "flat".

HINT: As always, we should follow the four-step plan for solving this problem.
STEP 1: FBD. Here, draw a free body diagram of the disk.
STEP 2: Kinetics (here, linear and angular impulse momentum equations).
STEP 3: Kinematics. Slipping ceases when the velocity of the contact point on the disk with the ground goes to zero. At that point: v_A = ω x r_A/C, where C is the point on the disk in contact with the ground.
STEP 4: Solve