Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS
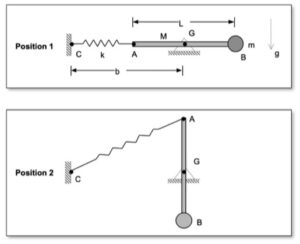
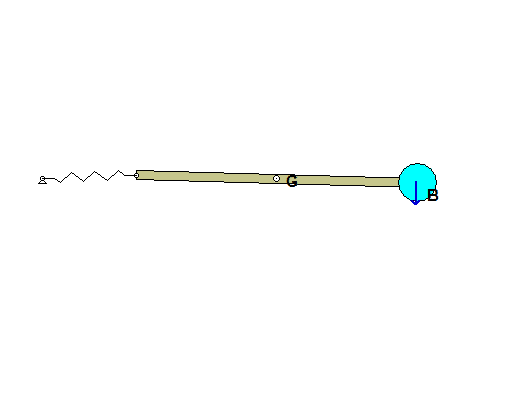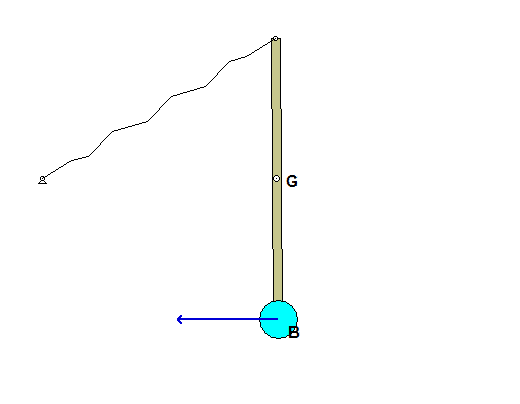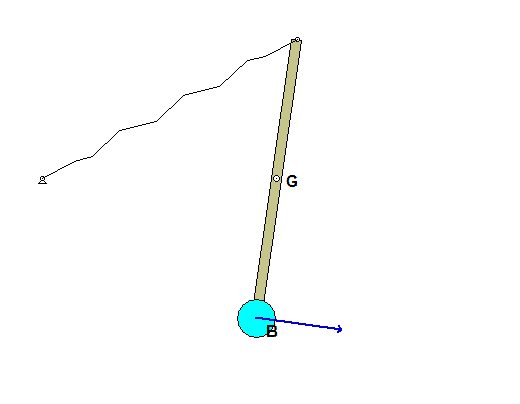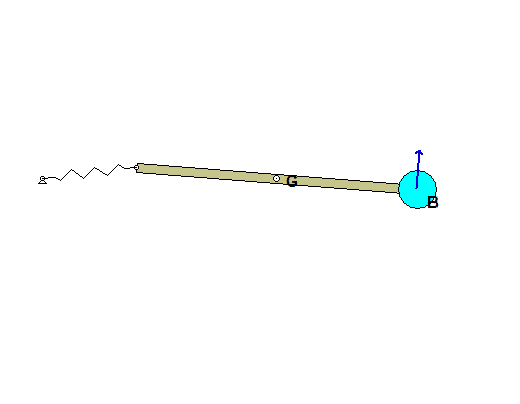
As the bar falls from its initial position, block B is moving downward. Once the bar has moved to a position where bar OA is aligned with section AC of the cable, the direction of motion for B is reversed and B begins moving upward. As can be seen in the animations, at some points in the subsequent motion, the cable goes in and out of being slack. What causes the cable to go slack?

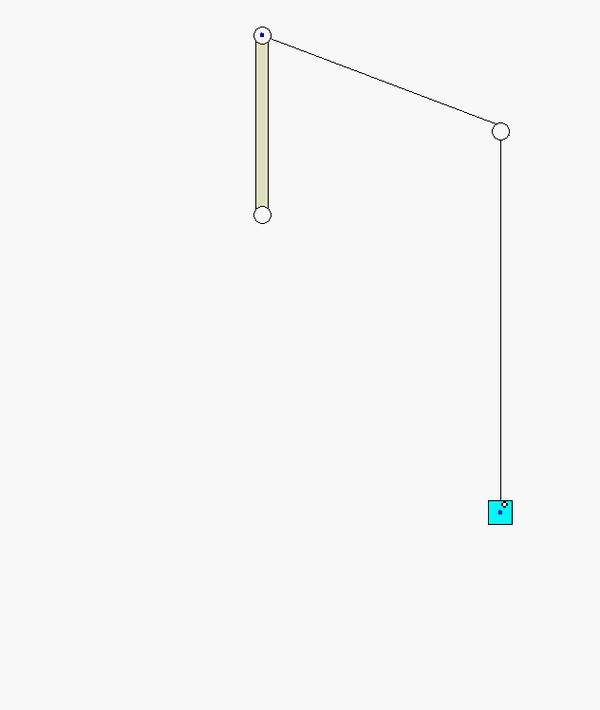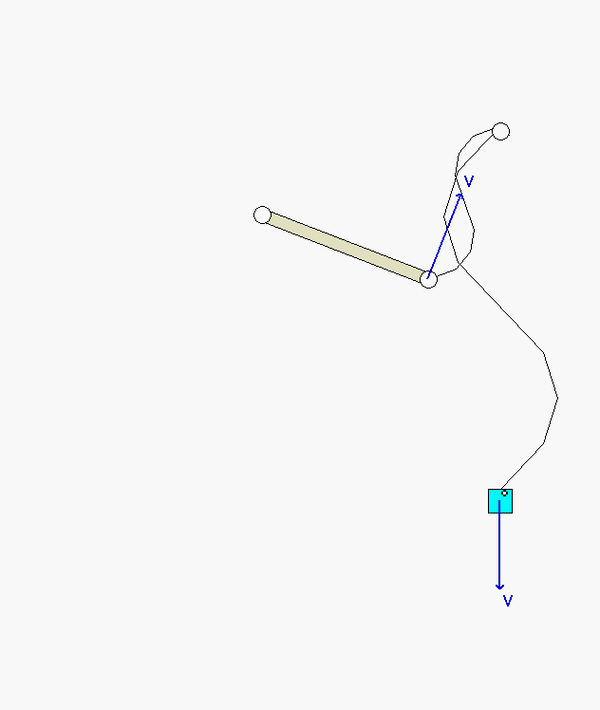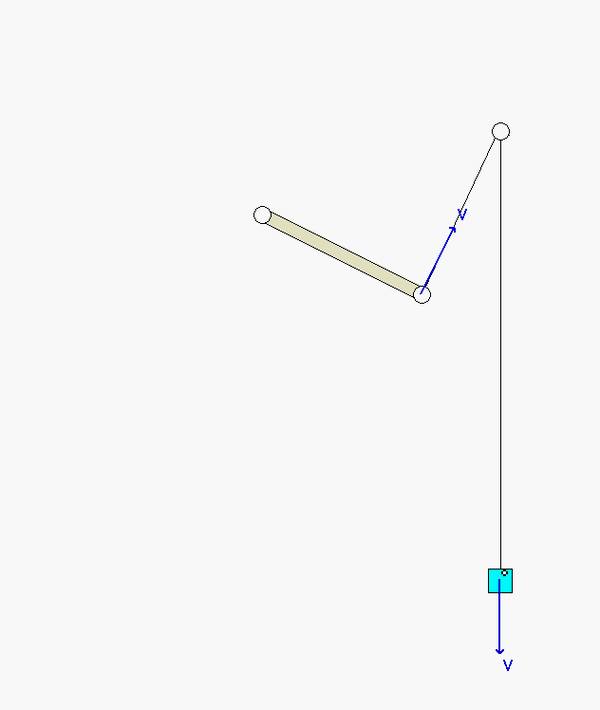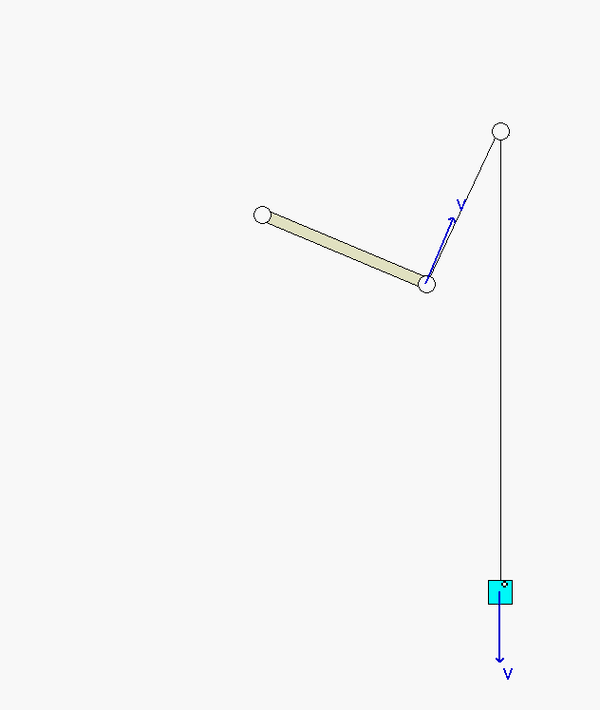
Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
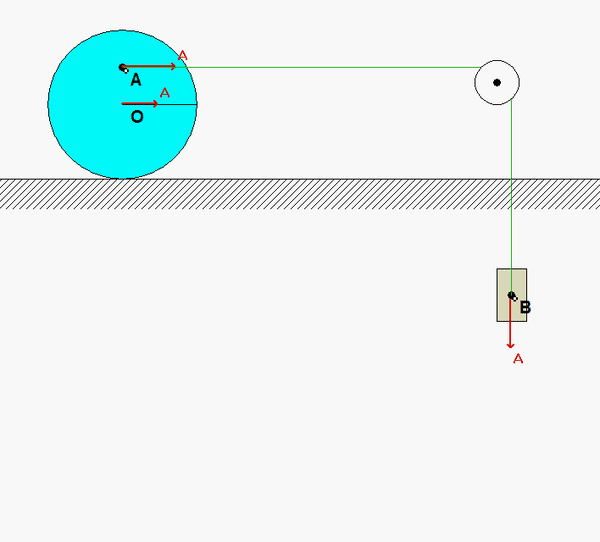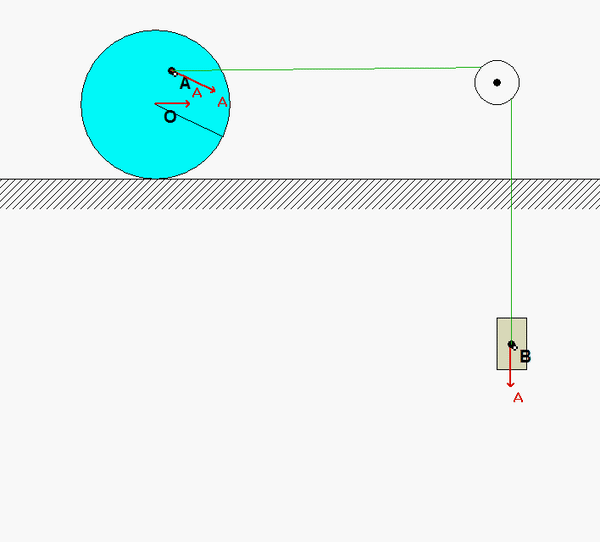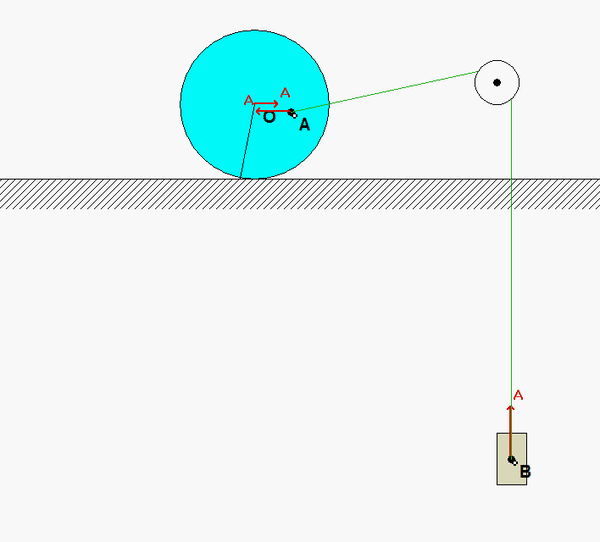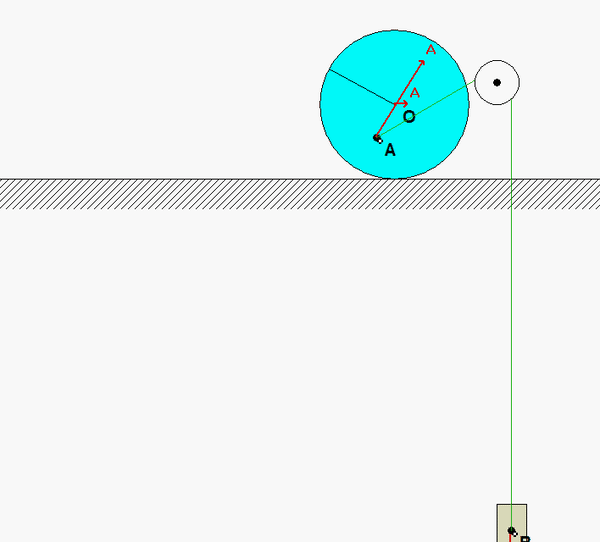
Draw a single free body diagram (FBD) of the system made up of bar OA and block B.

Step 2: Kinetics (work/energy)

• Looking at your FBD above, which forces, if any, do work that is not a part of the potential energy of the system? If there are none, then energy is conserved.
• Write down the individual kinetic energy expressions for bar OA and block B, and add together for the total KE of the system.
• Define your gravitational datum line. Write down the individual potential energy expressions for the bar OA and block B, and add together for the total PE of the system.

Step 3: Kinematics
Relate the speeds of A and B, and relate the speed of A to the angular speed of bar OA. It is recommended that you use some polar coordinates with the origin at C. See the notes that follow. Note that since the cable does not stretch, the value of R_dot is the same as the speed of B.

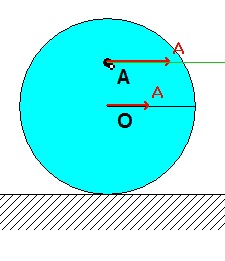
A freeze-frame of the above animation is shown below for the position where OA is horizontal. Note that the speed of A is larger than the speed of B, as is indicated in the kinematic analysis above.

Step 4: Solve
From your equations in Steps 2 and 3, solve for the velocity of block B at position 2.

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a single free body diagram (FBD) of the system made up of the drum, block A and the spring.

Step 2: Kinetics (work/energy)

• Looking at your FBD above, which forces, if any, do work that is not a part of the potential energy of the system? Does the force of friction at the no-slip contact point do work? If there are none, then energy is conserved.
• Write down the individual kinetic energy expressions for the drum and block A, and add together for the total KE of the system.
• Define your gravitational datum line. Write down the individual potential energy expressions for the drum block A and the spring, and add together for the total PE of the system.

Step 3: Kinematics
Relate the speed of A to the angular speed of the drum.

Step 4: Solve
From your equations in Steps 2 and 3, solve for the velocity of block A at position 2.

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a single free body diagram (FBD) of the bar and the particle.

Step 2: Kinetics (Work/energy)

• Looking at your FBD above, which forces, if any, do work that is not a part of the potential energy of the system? If there are none, then energy is conserved.
• Write down the individual contributions to the kinetic energy from the bar and particle, and add together for the total kinetic energy of the system.
• Define your gravitational datum line. Write down the individual contributions to potential energy from the bar, particle and spring, and add together for the total potential energy.

Step 3: Kinematics
Use the following rigid body kinematics equation to relate the angular velocity of the bar to the velocity of the particle B at position 2:

v_B= v_G + ω_AB x r_B/G

Step 4: Solve
From your equations in Steps 2 and 3, solve for the angular velocity of the bar.

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS

The animation below shows the motion of the wheel as it is being pulled up the incline. The animation shows the velocity of a number of points on the wheel. Think about the location of the instant center for the wheel as it rolls without slipping, and how this location affects the direction and magnitude of the velocities shown here.

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a free body diagram (FBD) of the wheel.

Step 2: Kinetics (Newton/Euler)

• Looking at your FBD above, which forces, if any, do work that is not a part of the potential energy of the system? Pay particular attention to the friction force at the no-slip point on the wheel - does it do work? How do you find the work done by the applied force F?
• Write down the kinetic energy of the wheel. Recall that the expression the KE for the planar motion of a rigid body is: T = 0.5*m*v_A² + 0.5*I_A*ω², where A is either the center of mass or a fixed point (fixed points include instant centers). So, in this case you can use either O or the no-slip contact point (let's call that point C).
• Define your gravitational datum line. Write down the potential energy for the wheel.

Step 3: Kinematics
Use the IC approach to relate the velocity of the point on the wheel where the cable comes off (call that point A) to the angular velocity of the wheel. Or, instead, use the following rigid body kinematics equation:

v_A= v_C + ω x r_A/C

Through a time integration of the relationship between the speed of A and the angular velocity of the wheel, you can determine the distance through which F moves.

Step 4: Solve
From your equations in Steps 2 and 3, solve for the angular velocity of the wheel at position 2.

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS
A cable connects block B to point A on the interior of the disk. We want to know the angular acceleration of the disk on release from rest. Watch the animation of the motion of the disk. What do you see in terms of the relationship between the accelerations of points O and A at the instant of release? And, between the accelerations of points A and B?

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw individual free body diagrams (FBDs) of the disk and block.

Step 2: Kinetics (Newton/Euler)
Note that the no-slip contact point C will have, at most, an acceleration that points toward O. Because of this, we can use the following Euler equation for the disk: ΣM_C = I_Cα_disk.

Step 3: Kinematics
Since the Newton equation for the block requires us to relate the acceleration of block B to the angular acceleration of the disk through point A on the disk, we should use the following rigid body kinematics equation:

a_A= a_C + α_disk x r_A/C - ω_disk²r_A/C

where we know that the horizontal component of acceleration of the no-slip contact point C is zero.

Step 4: Solve
From your equations in Steps 2 and 3, solve for the angular acceleration of the disk.

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS
Link OA is pinned to ground at O. Slider B is constrained to move along a straight guide. Link AB, having negligible mass, connects point A on OA with slider B. With OA initially rotating CCW, and with a force F acting to the right on B, we want to know the initial acceleration of slider B.

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw individual free body diagrams (FBDs) of the OA and slider B. Note that since link AB has negligible mass and that it has forces acting at only two points, AB is a two-force member. Knowing that, what are the directions of the reaction forces on OA and on B due to link AB?

Step 2: Kinetics (Newton/Euler)
You need to use an Euler (moment) equation for link OA, and a Newton equation for slider B.

Step 3: Kinematics
At the instant shown, the velocity of A is in the same direction as the velocity of B. What does this say about the instant center of AB, and therefore about the angular velocity of AB?

You will need two acceleration equations: one for link OA, and one for link AB:

a_A = a_O + α_OA x r_A/O - ω_OA² r_A/O
a_A = a_B + α_AB x r_A/B - ω_AB² r_A/B

Please note that ω_OA is NOT known to be constant. Do not assume so. Combining the above kinematics equations will provide you with the relationships relating α_OA, α_AB and a_B.

Step 4: Solve
From your equations in Steps 2 and 3, solve for the acceleration of the slider B.

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS
There are two critical issues involved in solving this problem.

• One, is starting out with good free body diagrams. Recall from our lecture discussion that the Newton/Euler equations typically prefer INDIVIDUAL FBDs. Note this in the discussion of Step 1 below.
• Second, we need to be careful on signs in establishing our kinematics relating the acceleration of the two blocks to the angular acceleration of the pulley.

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw individual free body diagrams (FBDs) of the pulley and the two blocks. A single FBD of the entire system will not be useful here. Let's say that we employ a "standard" xy-coordinate system (with x to the right and y up) for all FBDs.

Step 2: Kinetics (Newton/Euler)
You will need an Euler (moment) equation of the pulley about point C. In addition, write down the Newton equations for the y-motion for each of the two blocks. Write down all three equations using the sign convention discussed above.

Step 3: Kinematics
Here is where we need to be careful with signs. Write down the rigid body kinematics equations relating the accelerations of A and B back to the pulley center C:

a_A = a_C + α x r_A/C - ω²r_A/C
a_B = a_C + α x r_B/C - ω²r_B/C

This pair of equations will provide you with the relationships among a_A, a_B and α. Take note of the signs involved in these equations.

Step 4: Solve
From your equations in Steps 2 and 3, solve for the angular acceleration of the pulley and the accelerations of the two blocks.

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS
A horizontal force is applied to the center of mass of the thin bar, with the bar attached to a block that is constrained to have horizontal motion. Here want to know the resulting angular acceleration of the bar.

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw individual free body diagrams (FBDs) of the bar and block.

Step 2: Kinetics (Newton/Euler)
Take care with your Euler (moment) equation. The point about which you write down the moment must be either the center of mass or a fixed point. For example, you can NOT write ΣM_A = I_Aα_AB  because A is neither a fixed point nor is it the center of mass.

Step 3: Kinematics
End A of the bar is constrained to move only in the horizontal direction. Since the Newton equation for the bar requires the usage of the acceleration of the center of mass G, you will also need to use a kinematics equation relating the acceleration of A to the acceleration of G:

a_G = a_A + α x r_G/A - ω²r_G/A

Combining the above kinematics equations will provide you with the relationships among a_Gx, a_Gy, a_A and α.

Step 4: Solve
From your equations in Steps 2 and 3, solve for the angular acceleration of the bar.

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS
With the length of cables AC and BD being the same, and with the cables being parallel for all motion, bar AB remains horizontal as it moves. Specifically, ω_AB = 0 for ALL time, and therefore α_AB = 0 always. (Note that ω_AB = 0 does not necessarily say that α_AB = 0, only if ω_AB = 0 for all time.) Do you see this in the animation?

Since the center of mass for the bar is not equally spaced between points A and B, the tensions in the cables are not the same. You can see this in the animation below.

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a free body diagram (FBD) of the bar.

Step 2: Kinetics (Newton/Euler)
Take care with your Euler (moment) equation. The point about which you write down the moment must be either the center of mass or a fixed point. For example, you can NOT write ΣM_A = I_Aα_AB  because A is neither a fixed point nor is it the center of mass.

Step 3: Kinematics
As discussed above, bar AB remains horizontal for all motion. What does the say about the path of the center of mass G of the bar? And, from that, what is the direction of the acceleration of G, a_G, at this instant?

Step 4: Solve
From your equations in Steps 2 and 3, solve for the tensions in the two cable. Your equations will contain three unknowns: T_AC, T_BD and a_G.

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS
The motion of the bar is constrained by the two horizontal and vertical guides for the ends of the bar. These constraints add to the complexity of the kinematics (Step 3) of your solution, as we will discuss below. Take particular note of the direction of the acceleration of the center of mass G of the bar as it moves.

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a free body diagram (FBD) of the bar.

Step 2: Kinetics (Newton/Euler)
Take care with your Euler (moment) equation. The point about which you write down the moment must be either the center of mass or a fixed point. For example, you can NOT write ΣM_A = I_Aα_AB  because A is neither a fixed point nor is it the center of mass.

Step 3: Kinematics
End A of the bar is constrained to move only in the vertical direction. The other end of the bar (let's call it B) is constrained to move only in the horizontal direction. The first part of your kinematics should be directed to relating the motion of A and B through the rigid body acceleration equation:

a_B = a_A + α x r_B/A - ω²r_B/A

Since the Newton equation for the bar requires the usage of the acceleration of the center of mass G, you will also need to use a kinematics equation relating the acceleration of either A or B to the acceleration of G. For example, you could use:

a_G = a_A + α x r_G/A - ω²r_G/A

Combining the above kinematics equations will provide you with the relationships among a_Gx, a_Gy and α.

Step 4: Solve
From your equations in Steps 2 and 3, solve for the reactions N_A and N_B acting at ends A and B of the bar.