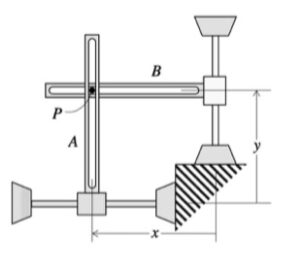
| Problem statement Solution video
|
DISCUSSION THREAD

Ask and answer questions here. You learn both ways.
DISCUSSION and HINTS
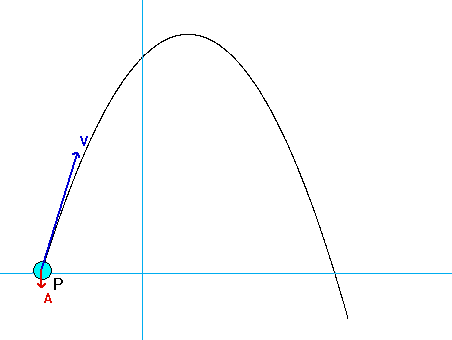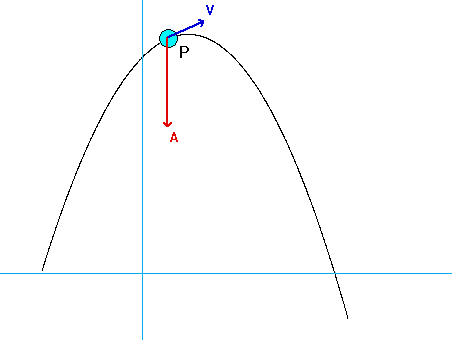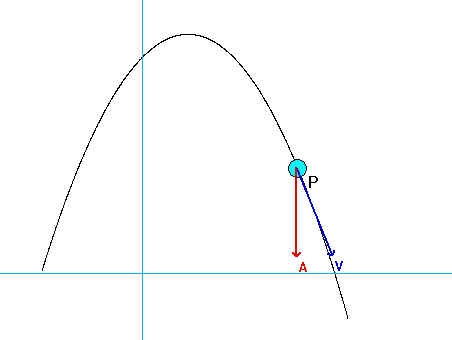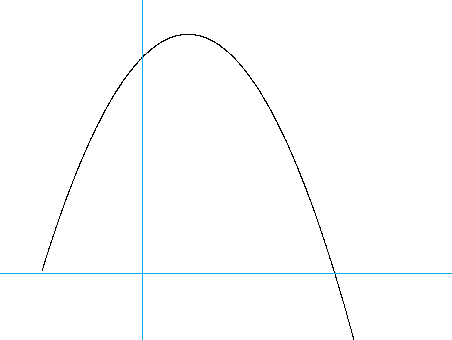
As expected, the acceleration of P has both non-zero tangential and normal components.
- From the equation provided for speed as a function of distance traveled, the speed of P is monotonically decreasing over the range of motion shown in the animation below. Therefore, the tangential component of acceleration always points "backward" of the direction of motion.
- The normal component decreases as P moves along the track since the speed of P is decreasing.
Can you see these two things in the animation below?
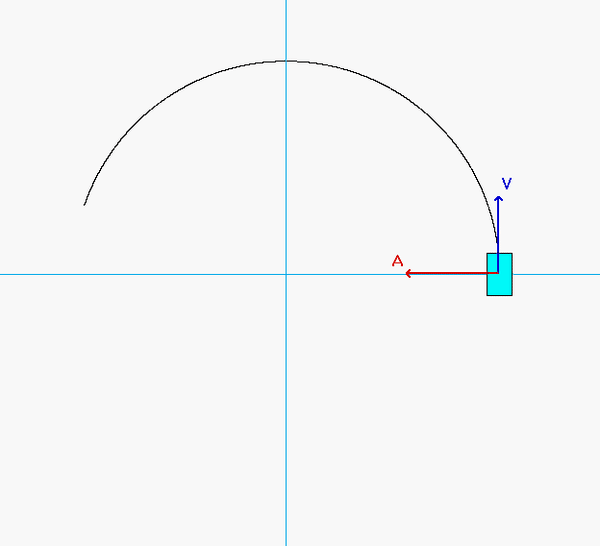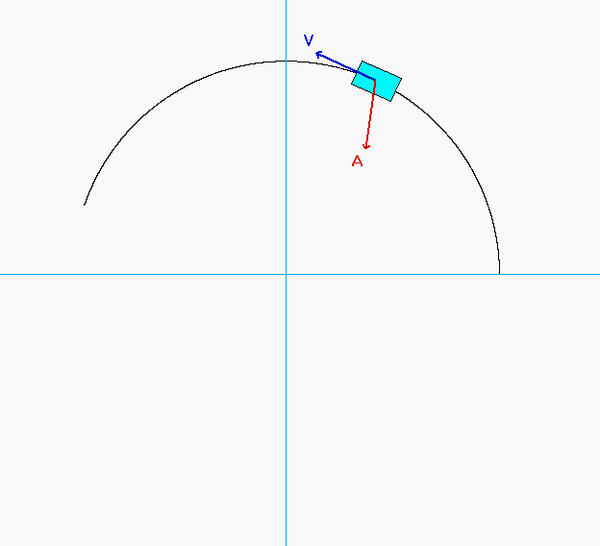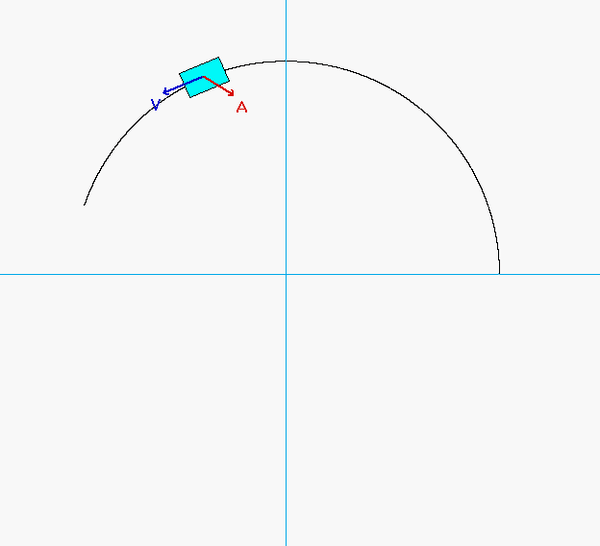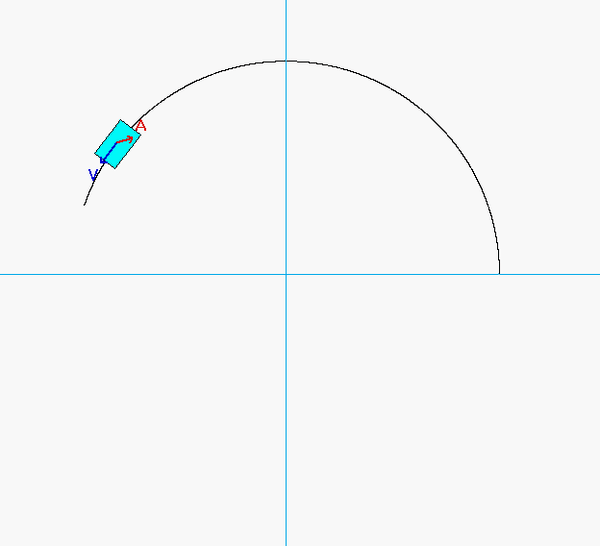
Recall that the general path description velocity and acceleration equations are given by the following:
v = v*et
a = v_dot*et + (v2/ρ)*en