NOTE: The view of the figure provided is that of the rod as seen from above the surface on which the rod lies.

Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.

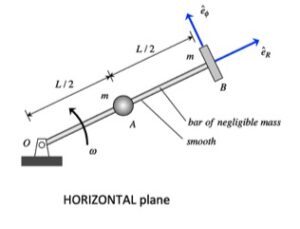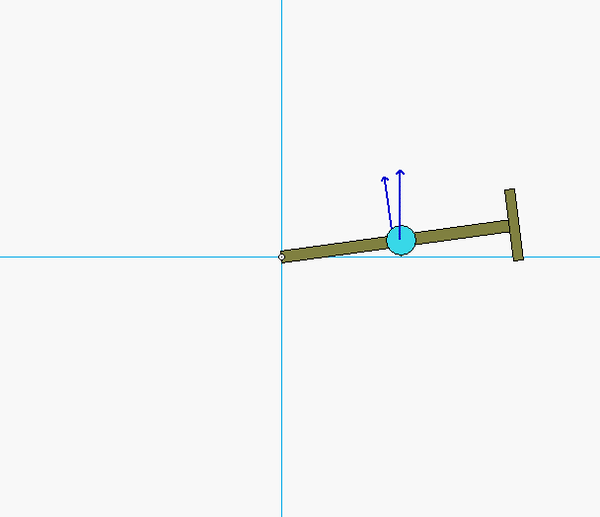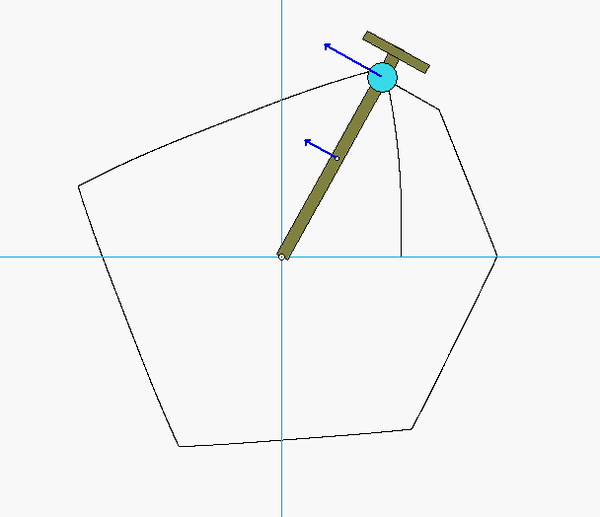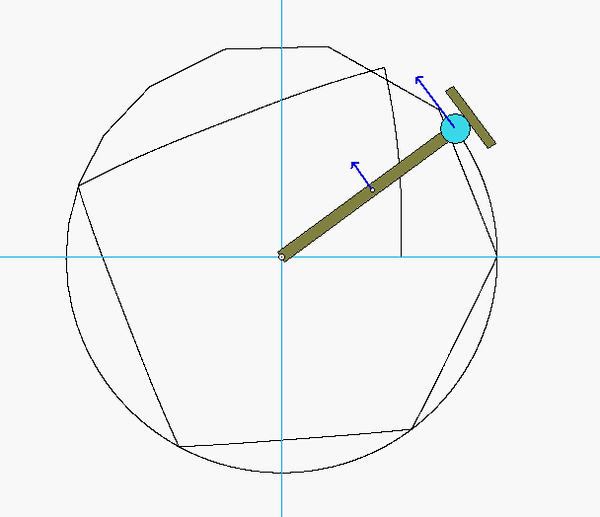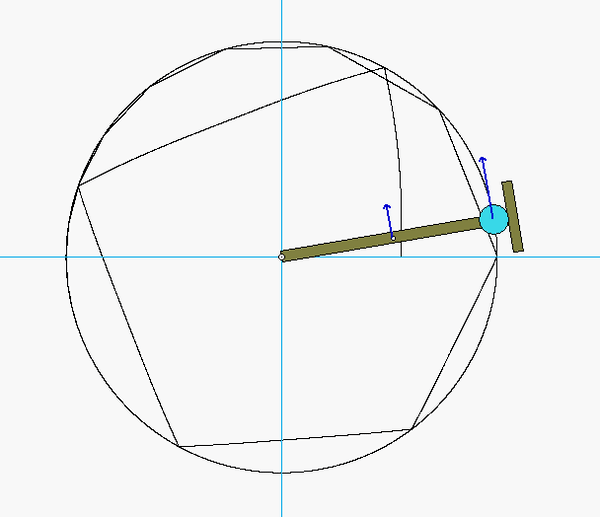
Discussion and hints:

Recall the following four-step plan outline in the lecture book and discussed in lecture:

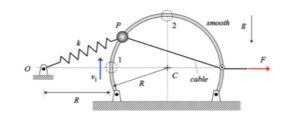
Step 1: FBDs
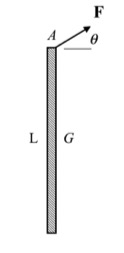
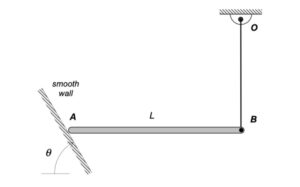
Draw a free body diagram of the bar.

Step 2: Kinetics (Newton/Euler)
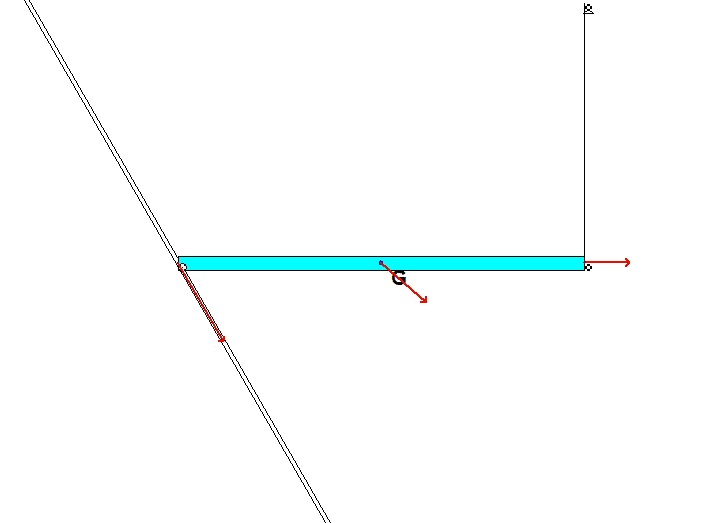
Write down the Newton/Euler equations for the bar using your FBD above. Take care in choosing the reference point for your moment equation. In order to use the "short form" of Euler's equation, this point should be either a fixed point or the body's center of mass. For this problem, there are no fixed points.

Step 3: Kinematics
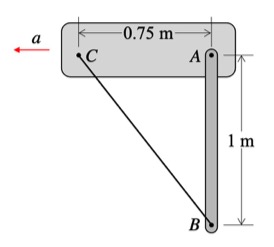
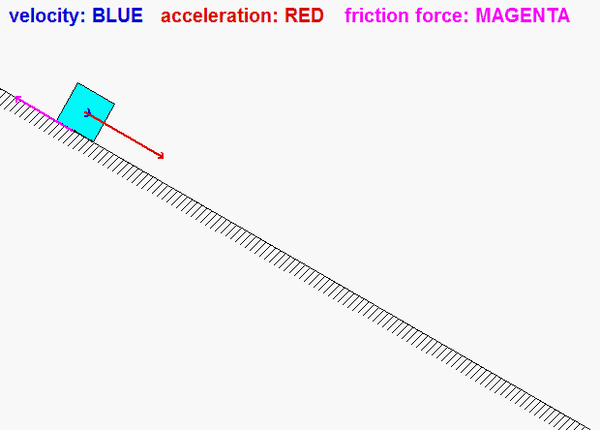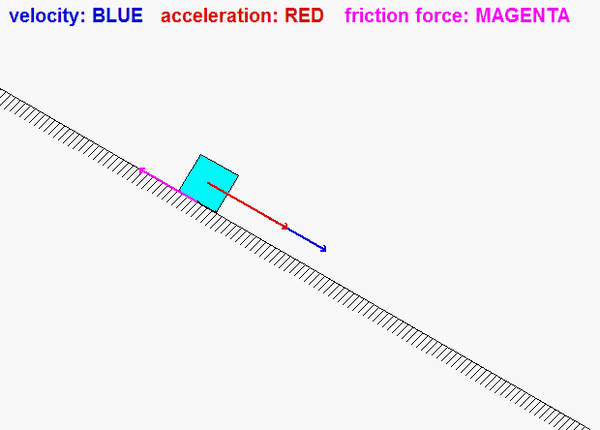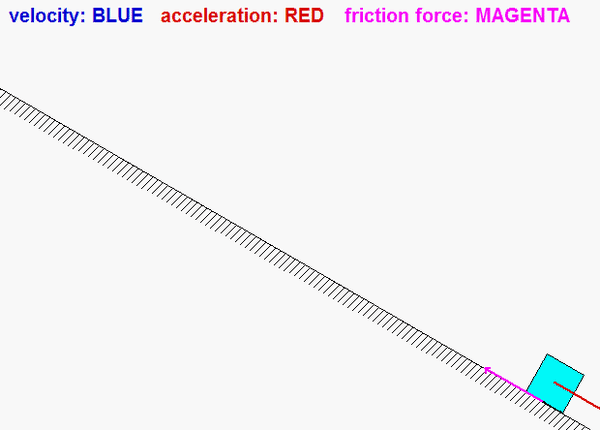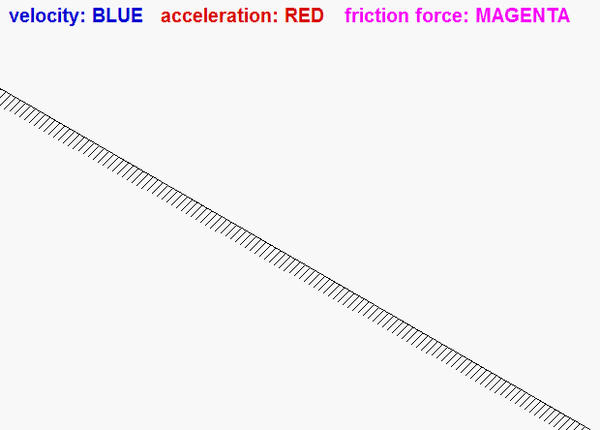
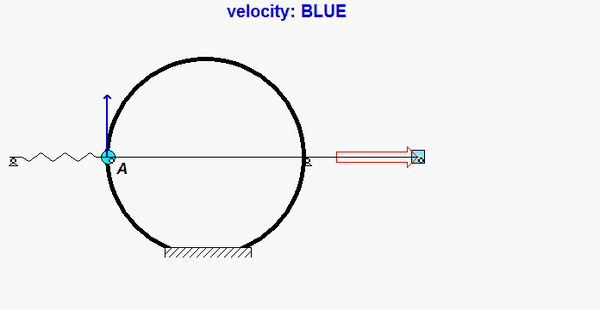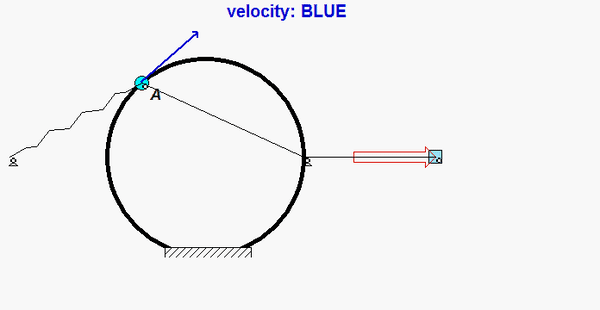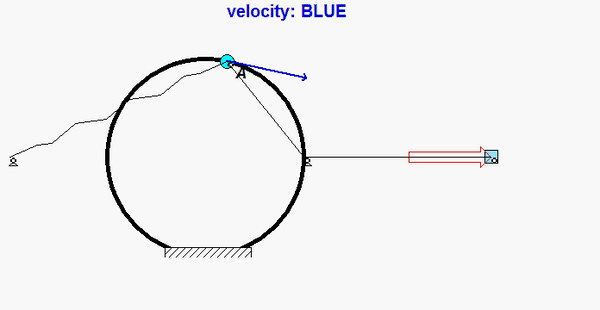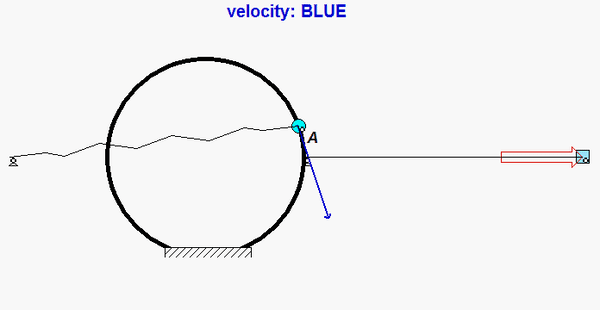
The paths of A and B are known: A travels on a straight path aligned with the inclined wall, and B travels on a circular path centered at O. Since the bar is released from rest, you know that the speeds of A and B are zero - therefore, the centripetal component of acceleration for each point is zero. This leaves the acceleration of points A and B tangent to their paths. (You can see this from the animation above for the instant when AB is horizontal.) It is recommended that you use two kinematics equations: one relating points A and B, and the other relating the center of mass G of the bar to either A or B.

Step 4: Solve
Solve your equations above for the tension in cable BO.

Any questions?

Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.

NOTE: The system moves in a horizontal plane.

DISCUSSION
Using the four-step plan:
STEP 1: Free body diagram (FBD) - Draw an FBD of bar AB.
STEP 2: Kinetics - Write down the Newton/Euler equations for the bar based on your FBD above. For the "short form" of the Euler equation, please note that you are constrained to using a moment about the center of mass G since there are no fixed points on AB; that is, you must use ΣM_G = I_G α.
STEP 3: Kinematics - With the inextensible cable being taut, all points on the rigid body AB have the same acceleration, and the angular acceleration of AB is zero: α = 0.
STEP 4: Solve - Use the equations from STEPS 2 and 3 to solve for the tension in the cable and the reaction at on the bar at A.

Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.

DISCUSSION

As P moves along the rough incline, the friction force will always oppose the motion of the block. As you see above, the friction force points up the incline as the velocity of the block points down the incline. Be sure to capture this in your FBD.

Hints:
You should follow the four-step solution plan described in the lecture book, and as discussed in lecture:
Step 1: Free body diagram (FBD) - Draw an FBD of P alone.
Step 2: Kinetics - Write down Newton's 2nd law for P.
Step 3: Kinetics - Newton's 2nd law relates the forces acting on P to its acceleration. In this problem, you are asked to relate the speed of P to the distance that it travels along the incline. To this end, it is recommended that you use the chain rule to convert the acceleration to speed through x: a = v*(dv/dx).
Step 4: Solve - Solve for the speed through the integration of Newton's section law in terms of x.

Ask and answer questions below. You will learn from both asking and answering.

DISCUSSION

Since the problem asks for a relationship between the change of speed of P and the distance traveled by P, the work/energy equation is a natural method of choice. Recall that with the work/energy equation, we typically want to include as much in the system in order so that we can make as many forces to be workless, internal forces within the system. To this end, consider a system made up of P and the cable connected to P.

Hints:
You should follow the four-step solution plan described in the lecture book:
Step 1: Free body diagram (FBD) - Draw an FBD of the system made up of P and the cable. Which forces in your FBD do work on the system?
Step 2: Kinetics - Write down the work/energy equation for P, and the terms included in this equation.
Step 3: Kinetics - In order to determine the  work done on the system by the applied force F, you need to find the distance traveled by the end of the cable as P moves from position 1 to position 2. HINT: This distance is equal to the amount of cable that is pulled over the pulley as P moves from position 1 to position 2.
Step 4: Solve - Solve for the final speed of P at position 2.

Ask and answer questions below. You will learn from both asking and answering.

Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.

You are asked to investigate the dynamics of this system during the time from release through to the time of immediately after when A strikes B.

• Divide this time of investigation into two segments: 1 to 2, and 2 to 3.
• From times 1 to 2, A slides outward on the arm until it almost impacts B. During this time, angular momentum of A+B+arm  is conserved, as well energy for that same system is conserved.
• From times 2 to 3, A impacts B. During this time, angular momentum of A+B+arm is conserved; however, due to the impact, energy is NOT conserved. Instead, we will use the coefficient of restitution relating the change in radial velocity for A as the second equation.

HINTS:

STEP 1 - FBD: Draw a SINGLE free body diagram (FBD) of the system of A+B+arm.
STEP 2 - Kinetics: The only force that you will see acting on this system during the full range of time from 1 to 3 is the support force at O. Because this forces acting through point O, angular momentum  about O is conserved throughout. During the pre-impact time of 1 to 2, also write down a conservation of energy equation. During the impact time of 2 to 3, write down the COR equation involving only the radial components of velocity for A.
STEP 3 - Kinematics: At Instant 1, A and B have only e_θ components of velocity. For Instants 2 and 3, A has both e_r and e_θ components of velocity, and B has only e_θ components of velocity.
STEP 4 - Solve. 

Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.

Discussion

You are asked to investigate the dynamics of this system during the short time of impact of P with A.

• It is suggested that you consider a system made up of A+P+bar (make the system "big").
• Draw a free body diagram (FBD) of this system.
• For this system, linear momentum is NOT conserved since there are non-zero reaction forces at O.
• Furthermore, energy is NOT conserved since there is an impact of P with A during that time.
• From your FBD of the system, you see that the moment about the fixed point O is zero. What does this say about the angular momentum of the system about O during impact? (Answer: It is conserved!)

HINTS:

STEP 1 - FBD: Draw a SINGLE free body diagram (FBD) of the system of A+P+bar.
STEP 2 - Kinetics:  Consider the discussion above in regard to conservation of angular momentum about point O. Recall how to calculate the angular momentum about a point for a particle.
STEP 3 - Kinematics: At Instant 2, the P sticks to A: v_P2 = v_A2.
STEP 4 - Solve. 

Ask and answer questions here. You learn both ways.

DISCUSSION and HINTS

Recall the definition of angular momentum of a particle P (of mass m) about a fixed point O:  H_O = m r_P/O x v_P.

For this problem, use this equation to find the angular momentum for each particle and add these together. As you work the problem, consider the number of cancellations that occur among these terms and consider why these cancellations occur. This will help you get insights on the meanings of angular momentum.