September 18, 2019
‘Poor man’s qubit’ can solve quantum problems without going quantum
Researchers demonstrate the first hardware for a ‘probabilistic computer’
 For the first time, researchers have demonstrated a way to build a probabilistic computer. This circuit includes a modified version of a magnetoresistive random-access memory device (red) to interconnect eight p-bits. (Purdue University image/Ahmed Zeeshan Pervaiz)
Download image
For the first time, researchers have demonstrated a way to build a probabilistic computer. This circuit includes a modified version of a magnetoresistive random-access memory device (red) to interconnect eight p-bits. (Purdue University image/Ahmed Zeeshan Pervaiz)
Download image
WEST LAFAYETTE, Ind. — It may still be decades before quantum computers are ready to solve problems that today’s classical computers aren’t fast or efficient enough to solve, but the emerging “probabilistic computer” could bridge the gap between classical and quantum computing.
Engineers at Purdue University and Tohoku University in Japan have built the first hardware to demonstrate how the fundamental units of what would be a probabilistic computer – called p-bits – are capable of performing a calculation that quantum computers would usually be called upon to perform.
The study, published in Nature on Wednesday (Sept. 18), introduces a device that serves as a basis for building probabilistic computers to more efficiently solve problems in areas such as drug research, encryption and cybersecurity, financial services, data analysis and supply chain logistics.
Today’s computers store and use information in the form of zeroes and ones called bits. Quantum computers use qubits that can be both zero and one at the same time. In 2017, a Purdue research group led by Supriyo Datta, the university’s Thomas Duncan Distinguished Professor of Electrical and Computer Engineering, proposed the idea of a probabilistic computer using p-bits that can be either zero or one at any given time and fluctuate rapidly between the two.
“There is a useful subset of problems solvable with qubits that can also be solved with p-bits. You might say that a p-bit is a ‘poor man’s qubit,’” Datta said.
Whereas qubits need really cold temperatures to operate, p-bits work at room temperature like today’s electronics, so existing hardware could be adapted to build a probabilistic computer, the researchers say.
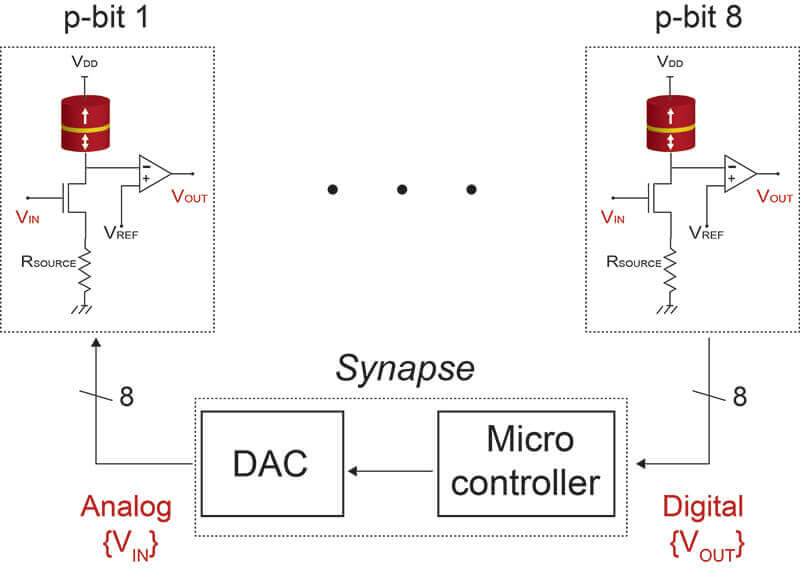
The team built a device that is a modified version of magnetoresistive random-access memory, or MRAM, which some types of computers use today to store information. The technology uses the orientation of magnets to create states of resistance corresponding to zero or one.
Tohoku University researchers William Borders, Shusuke Fukami and Hideo Ohno altered an MRAM device, making it intentionally unstable to better facilitate the ability of p-bits to fluctuate. Purdue researchers combined this device with a transistor to build a three-terminal unit whose fluctuations could be controlled. Eight such p-bit units were interconnected to build a probabilistic computer.
The circuit successfully solved what is often considered a “quantum” problem: Breaking down, or factoring, numbers such as 35,161 and 945 into smaller numbers, a calculation known as integer factorization. These calculations are well within the capabilities of today’s classical computers, but the researchers believe that the probabilistic approach demonstrated in this paper would take up much less space and energy.
“On a chip, this circuit would take up the same area as a transistor, but perform a function that would have taken thousands of transistors to perform. It also operates in a manner that could speed up calculation through the parallel operation of a large number of p-bits,” said Ahmed Zeeshan Pervaiz, a Ph.D. student in electrical and computer engineering at Purdue.
Realistically, hundreds of p-bits would be needed to solve bigger problems – but that’s not too far off, the researchers say.
“In the near future, p-bits could better help a machine to learn like a human does or optimize a route for goods to travel to market,” said Kerem Camsari, a Purdue postdoctoral associate in electrical and computer engineering.
The Purdue group is associated with the Discovery Park Center for Computing Advances by Probabilistic Spin Logic led by Joerg Appenzeller, who also recently annnounced the launch of Purdue-P. A patent application for this technology has been filed through the Purdue Research Foundation Office of Technology Commercialization.
The work was partially supported by the Defense Advanced Research Projects Agency; the Semiconductor Research Corp.; Japan’s Council for Science, Technology and Innovation; the Japan Society for the Promotion of Science; and the Research Institute of Electrical Communication of Tohoku University.
Media contact: Amy Patterson Neubert, 765-494-9723, apatterson@purdue.edu
Writer: Kayla Wiles, 765-494-2432, wiles5@purdue.edu
Sources:
Supriyo Datta, 765-494-3511, datta@purdue.edu
Ahmed Zeeshan Pervaiz, apervaiz@purdue.edu
Note to Journalists: For a copy of the paper, please contact Amy Patterson Neubert, Purdue News Service, at apatterson@purdue.edu.
ABSTRACT
Integer Factorization Using Stochastic Magnetic Tunnel Functions
William A. Borders1,8 , Ahmed Z. Pervaiz2,8 , Shunsuke Fukami1,3,4,5,6,7, Kerem Y. Camsari2, Hideo Ohno1,3,4,5,6,7, Supriyo Datta2
1Laboratory for Nanoelectronics and Spintronics, Research Institute of Electrical Communication, Tohoku University, Sendai, Japan
2School of Electrical and Computer Engineering, Purdue University, West Lafayette, IN, USA
3Center for Spintronics Integrated Systems, Tohoku University, Sendai, Japan
4Center for Innovative Integrated Electronic Systems, Tohoku University, Sendai, Japan
5Center for Spintronics Research Network, Tohoku University, Sendai, Japan
6Center for Science and Innovation in Spintronics (Core Research Cluster), Tohoku University, Sendai, Japan
7WPI-Advanced Institute for Materials Research, Tohoku University, Sendai, Japan
DOI: 10.1038/s41586-019-1557-9
Conventional computers operate deterministically using strings of zeros and ones called bits to represent information in binary code. Despite the evolution of conventional computers into sophisticated machines, there are many classes of problems they cannot efficiently address, including inference, invertible logic, sampling, and optimization, leading to considerable interest in alternative computing schemes. Quantum computing, which uses qubits to represent a superposition of O and I, can perform these tasks efficiently. However, decoherence and the current requirement for cryogenic operation, as well as the limited many-body interactions that can be implemented, pose considerable challenges. Probabilistic computing is another unconventional computation scheme that shares similar concepts with quantum computing but is not limited by the above challenges. The key role is played by a probabilistic bit-a p-bit-a robust, classical entity fluctuating in time between 0 and I, which interacts with other p-bits in the same system using principles inspired by neural networks. Here we present a proof-of-concept experiment for probabilistic computing using spintronics technology, and demonstrate integer factorization, an illustrative example of the optimization class of problems addressed by adiabatic and gated quantum computing. Nanoscale magnetic tunnel junctions showing stochastic behaviour are developed by modifying market-ready magnetoresistive random access memory technology and are used to implement three-terminal p-bits that operate at room temperature. The p-bits are electrically connected to form a functional asynchronous network, to which a modified adiabatic quantum computing algorithm that implements threeand four-body interactions is applied. Factorization of integers up to 945 is demonstrated with this rudimentary asynchronous probabilistic computer using eight correlated p-bits and the results show good agreement with theoretical predictions, thus providing a potentially scalable hardware approach to the difficult problems of optimization and sampling.
Related Website
Stochastic p-bits for invertible logic – Physical Review X

