| Problem statement Solution video |
DISCUSSION THREAD
Any questions??
Discussion and hints:
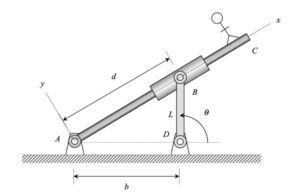
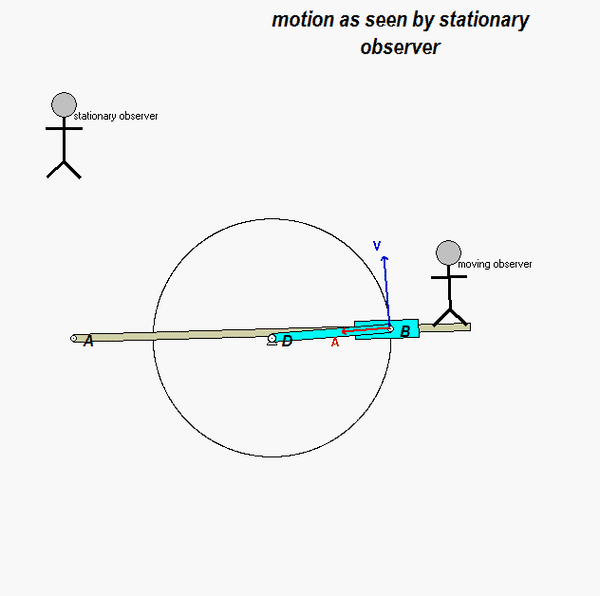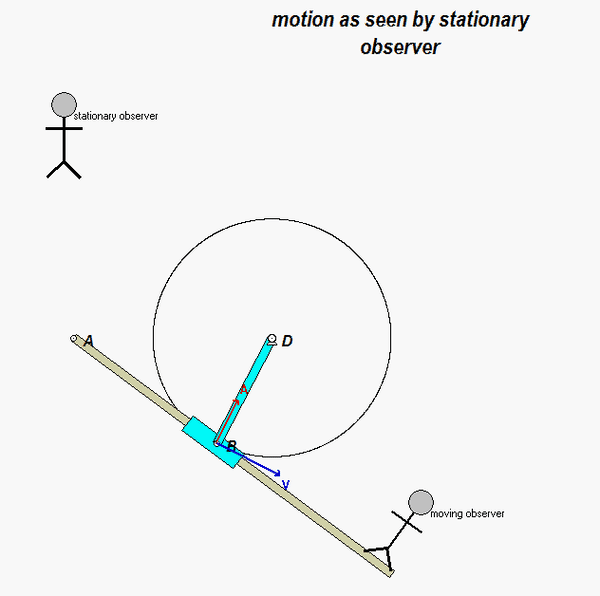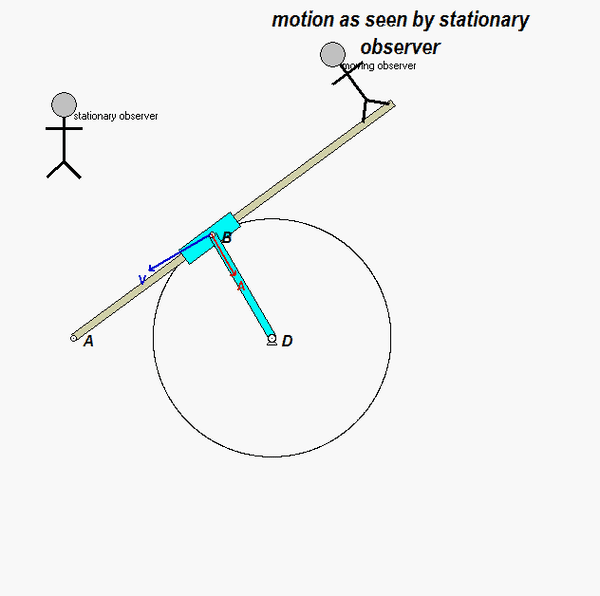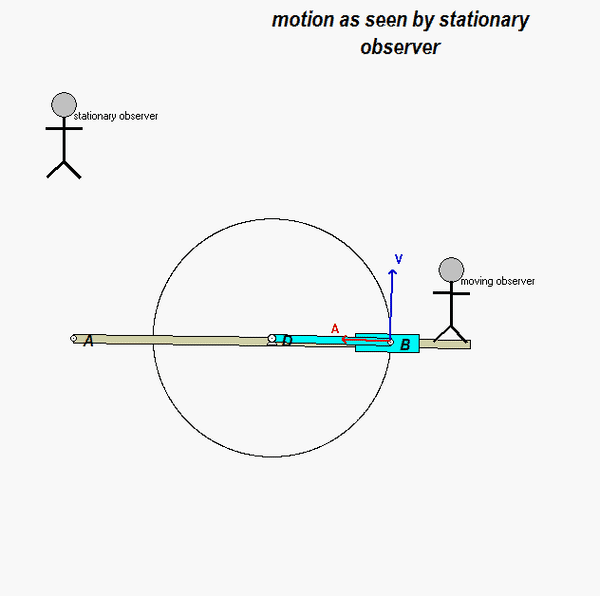
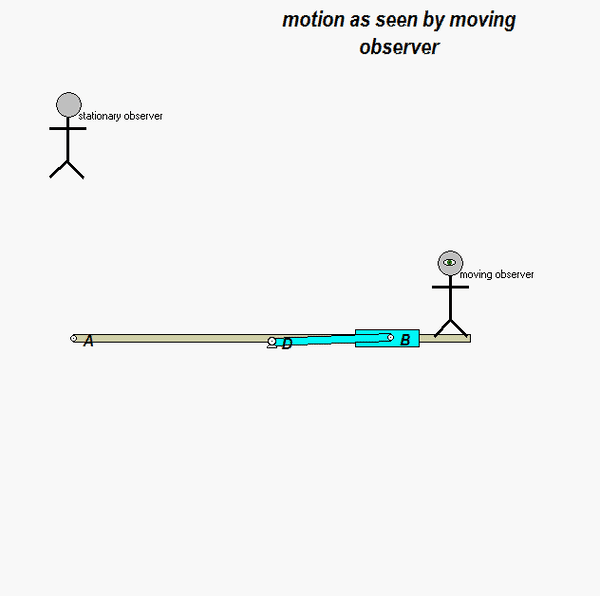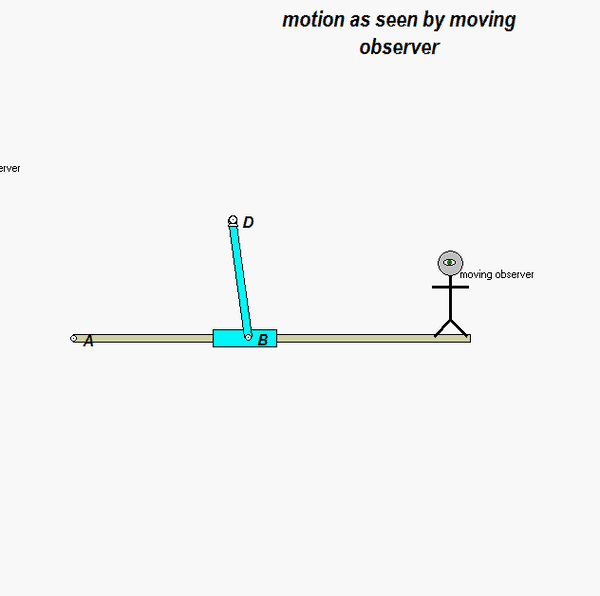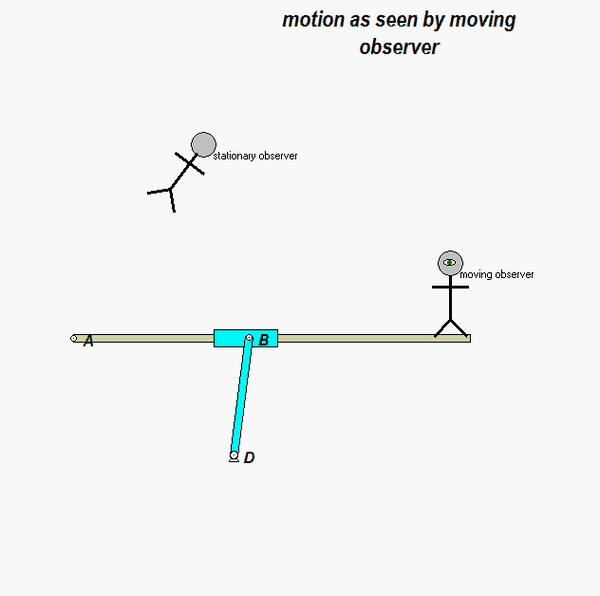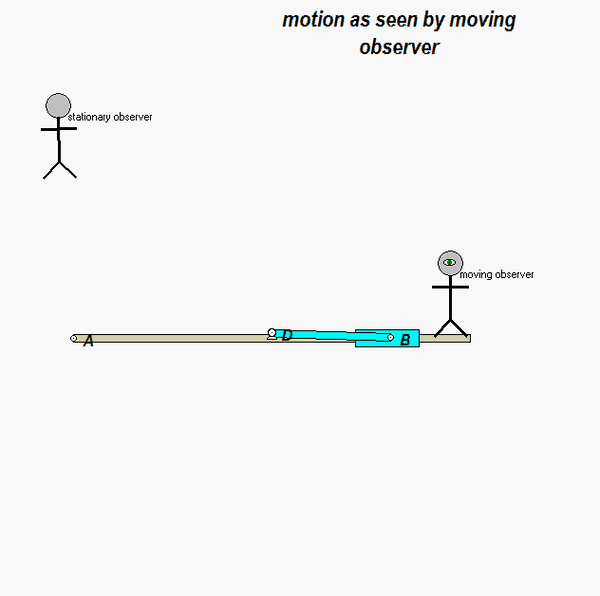
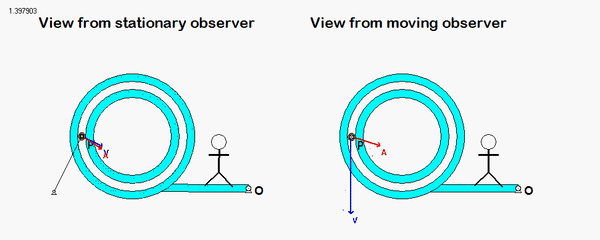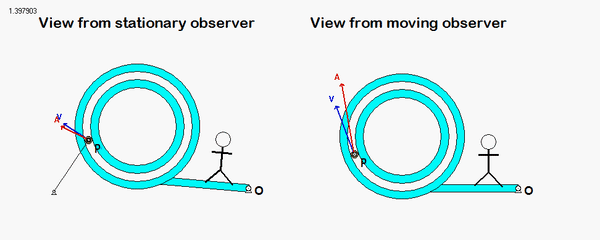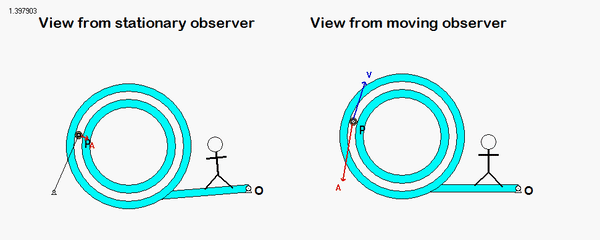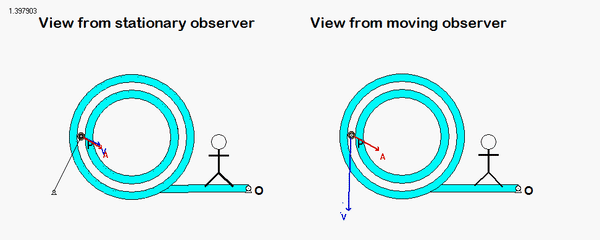
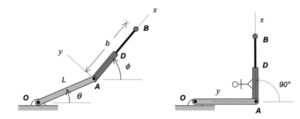
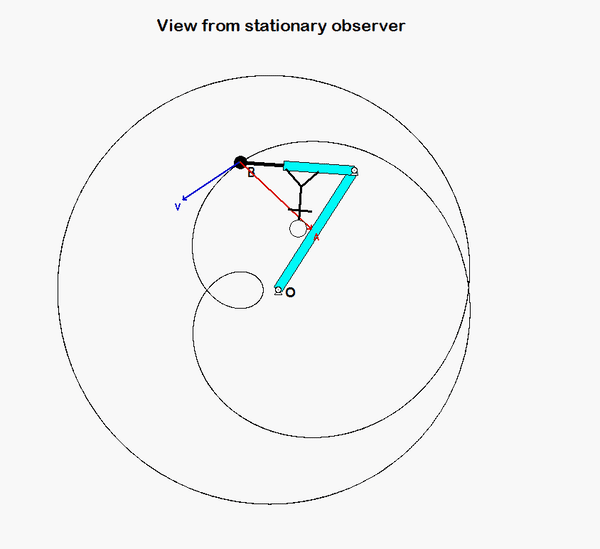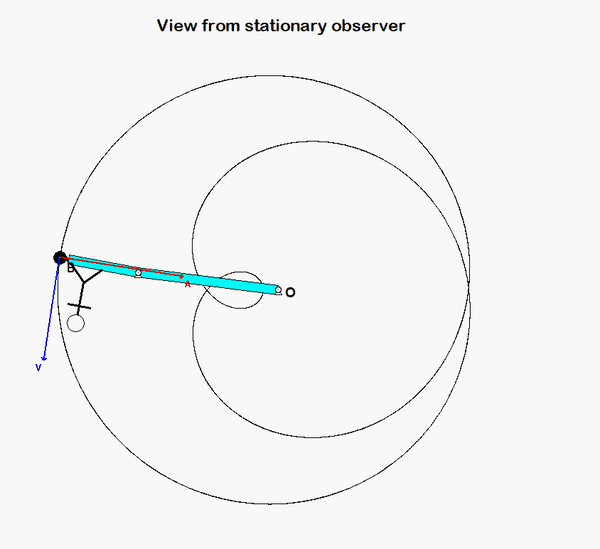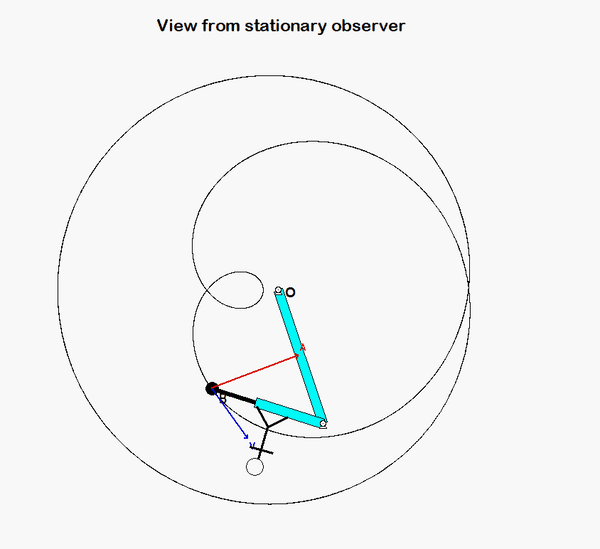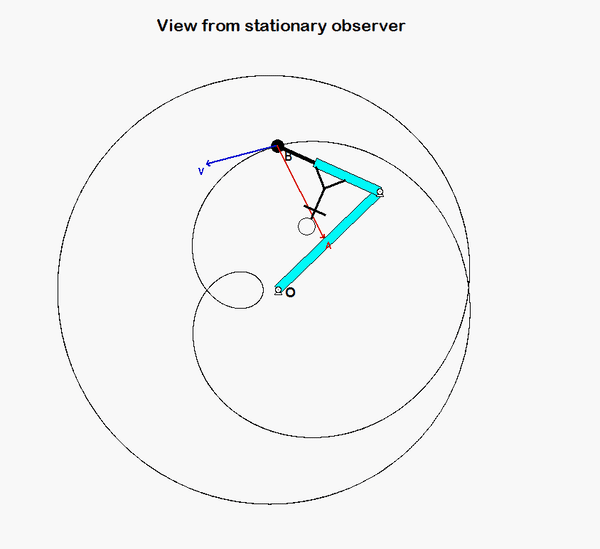
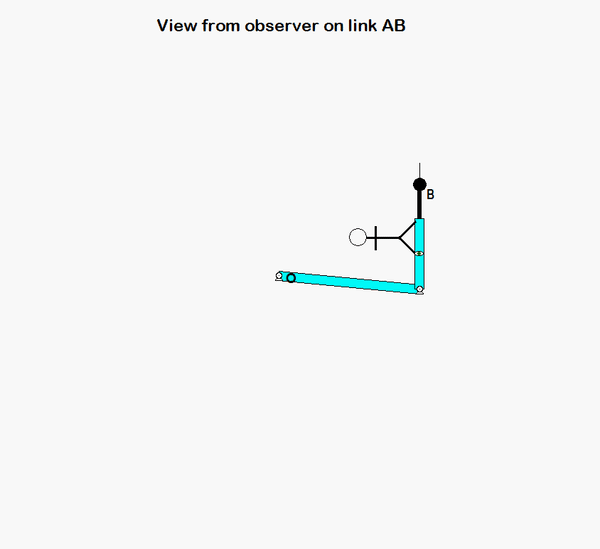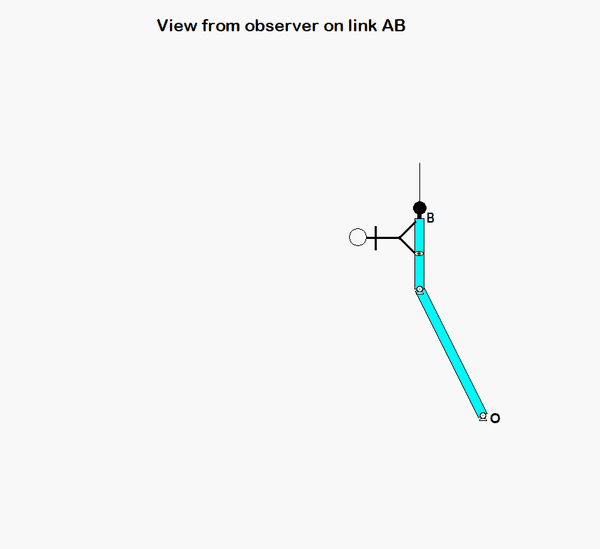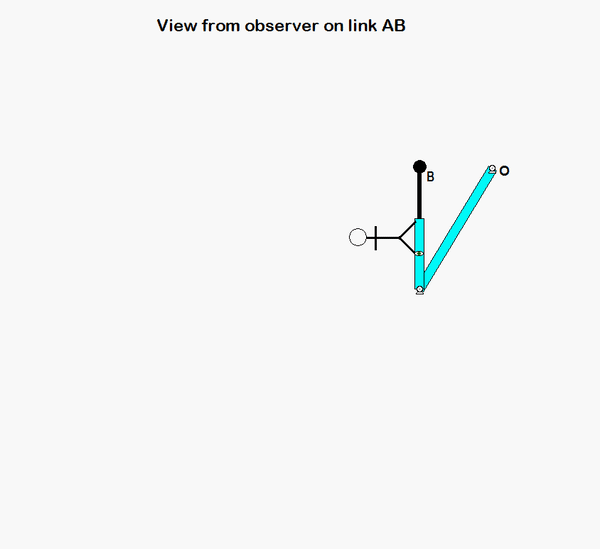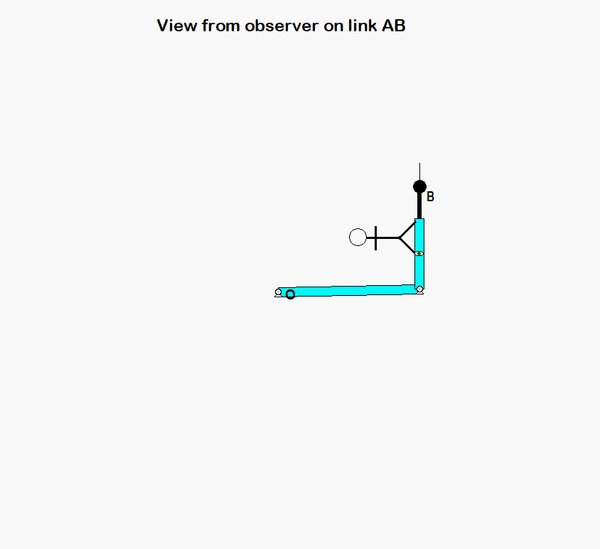
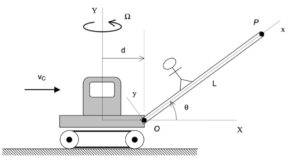
It is recommended that you use an observer attached to the boom. As we have discussed in class, your choice of observer directly affects four terms in the acceleration equation: ω and α (how the observer moves), and the relative velocity and relative acceleration terms (what the observer sees). Note that the remainder of the discussion here is based on having the observer attached to the boom.
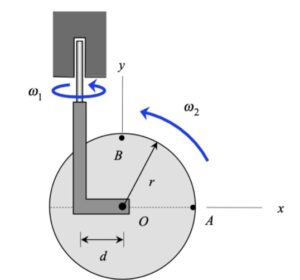
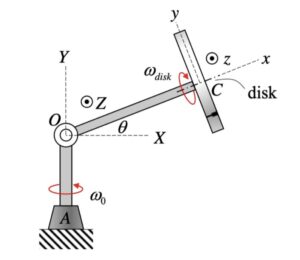
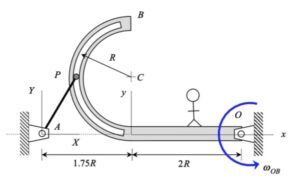
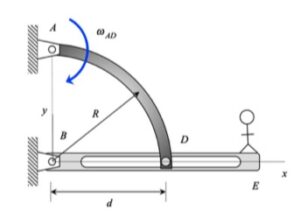
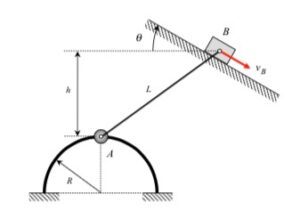
The boom shown above has TWO components of rotation:
- a rotation rate of Ω about a fixed axis (the “+” Y-axis), and,
- a rotation rate of θ_dot about a moving axis (the “+” z-axis)
(Be sure to make a clear distinction between the lower case and upper case symbols.)
Therefore, the angular velocity of the wheel is given by:
ω = Ω J + θ_dot k
The angular acceleration vector α is simply the time derivative of the angular velocity vector ω : α = dω/dt. In taking this time derivative,
- Recall that the J-axis is fixed. Since J is fixed, then dJ/dt = 0.
- Recall that the k-axis is NOT fixed. Knowing that, how do you find dk/dt?
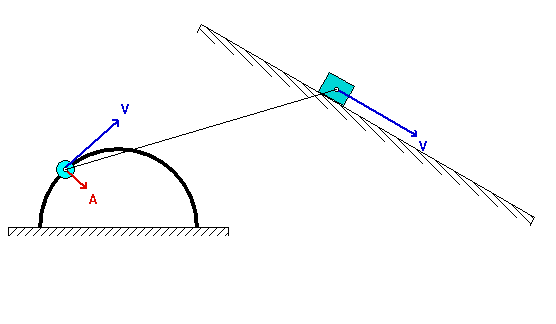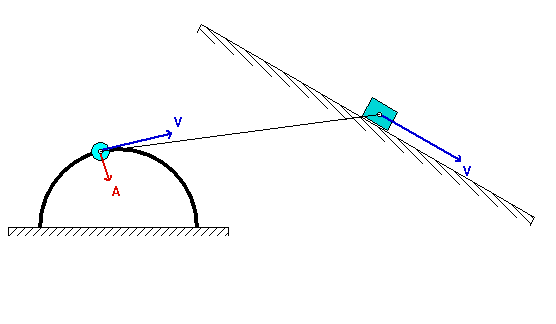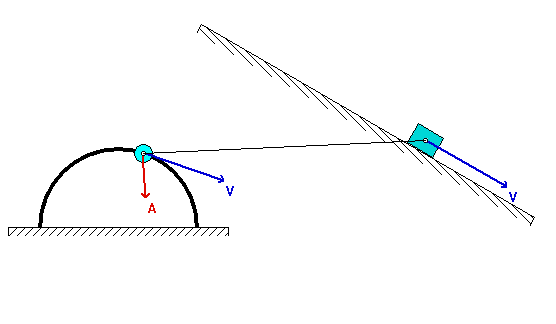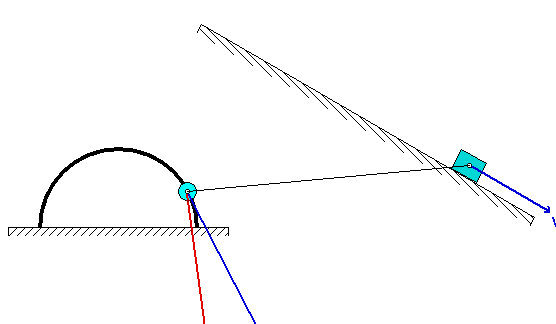
With the observer attached to the boom, what motion does the observer see for point P? That is, what are (vP/O)rel and (aP/O)rel?
NOTE: Pay particular attention to the motion of the reference point O. What path does O follow? And, based on that, how do you write down the acceleration vector of point O, aO?