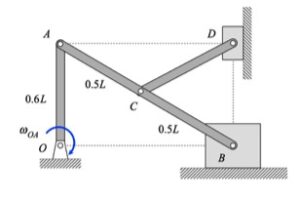
| Problem statement Summary sheet for 2D MRF kinematics-2 Solution video |
DISCUSSION THREAD
We encourage you to interact with your colleagues here in conversations about this homework problem.
Discussion and hints
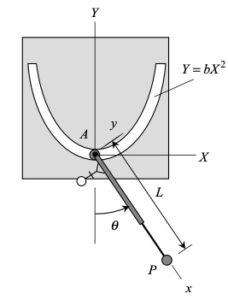
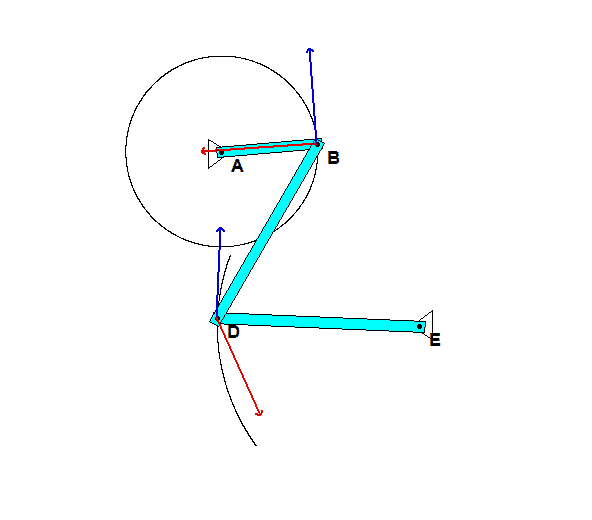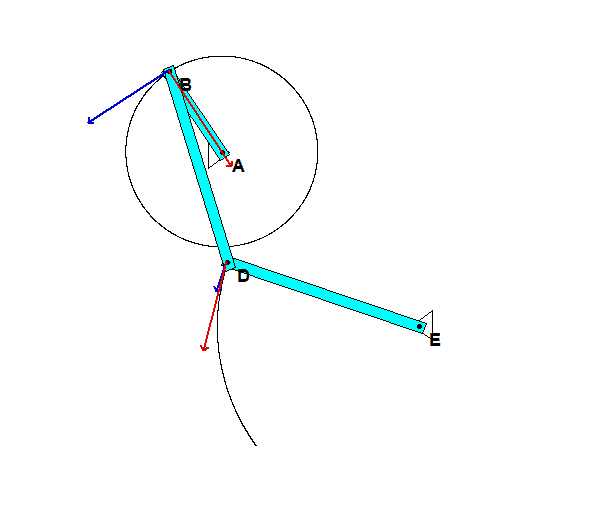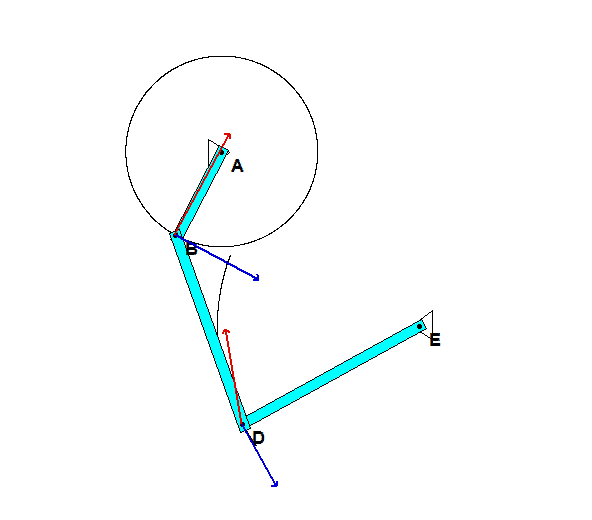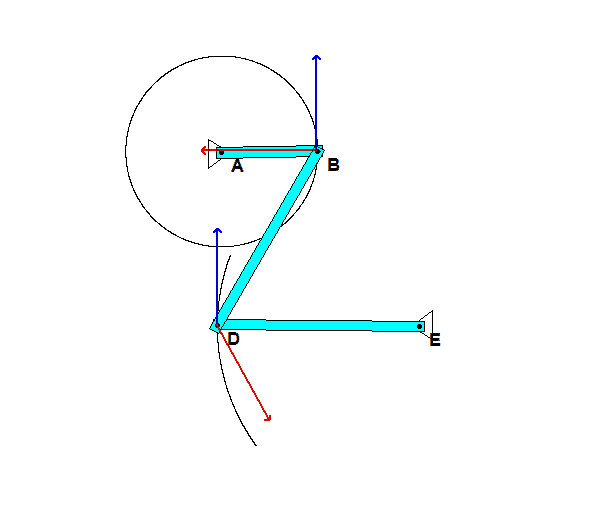
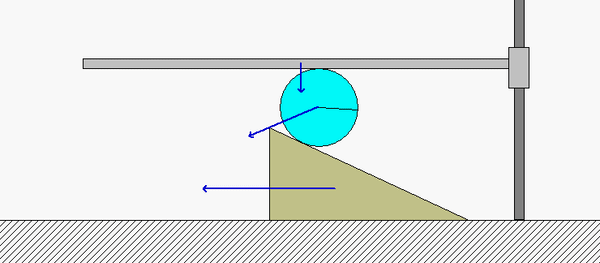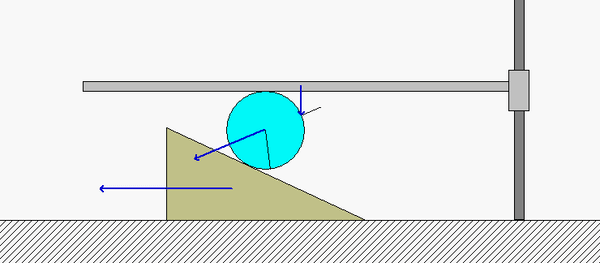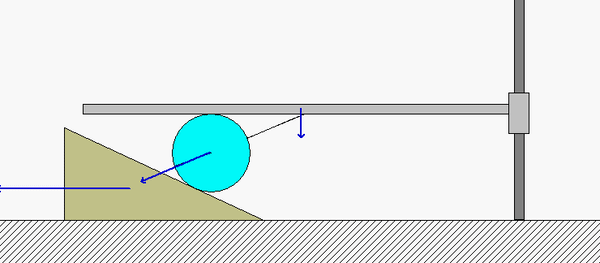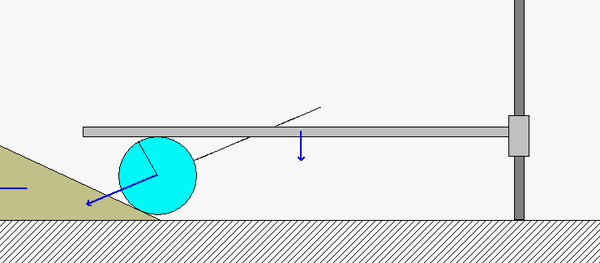
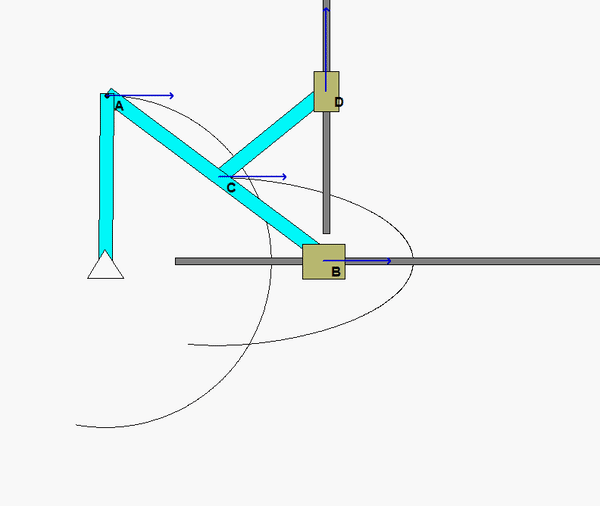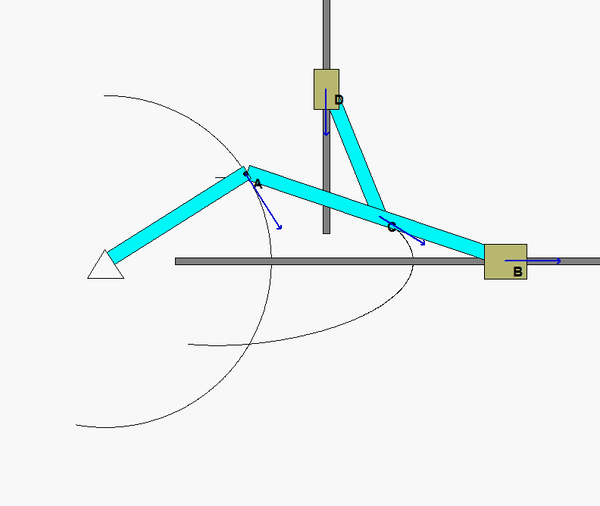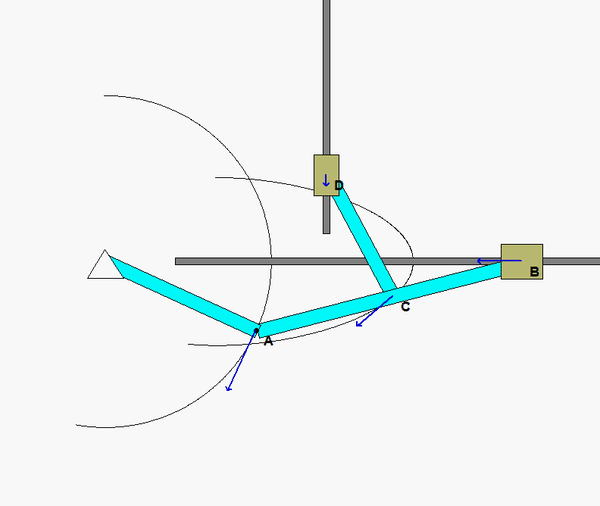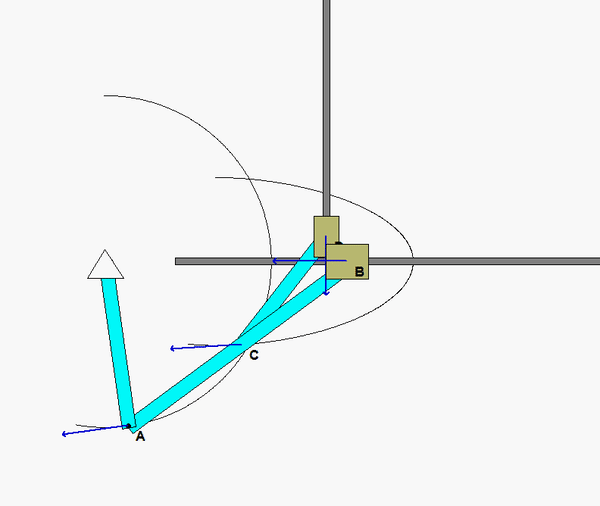
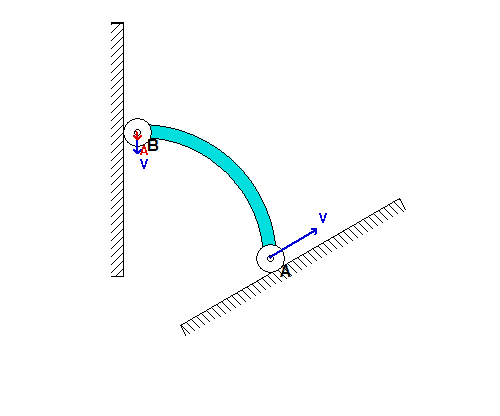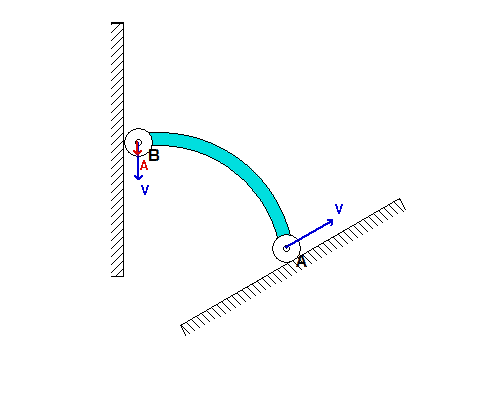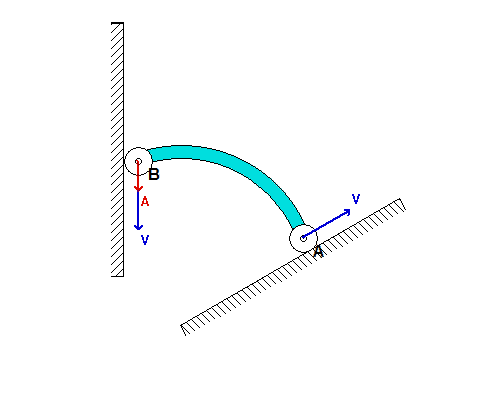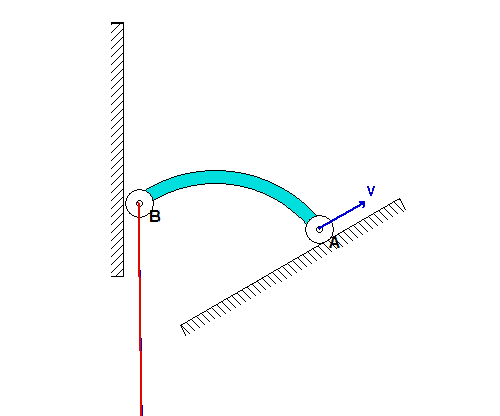
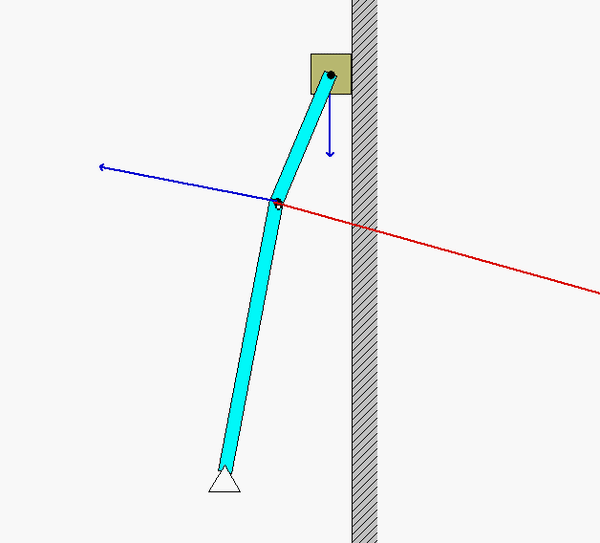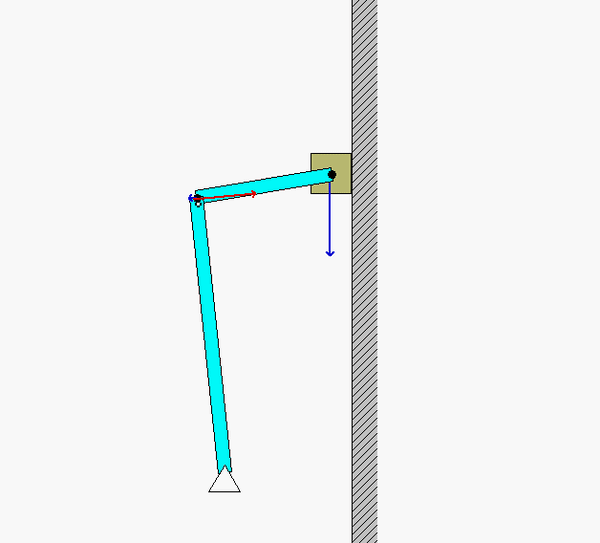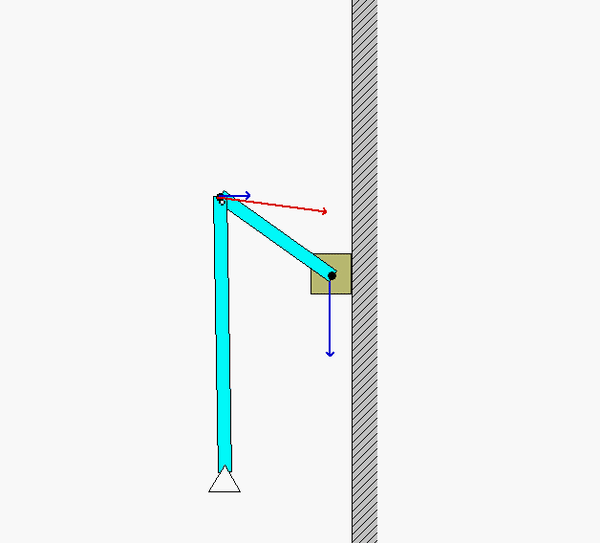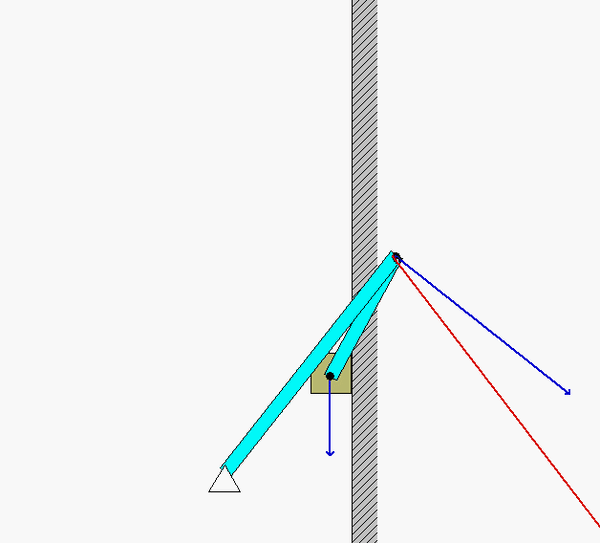
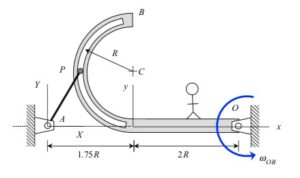
In order to create the animated GIFs shown below, a problem slightly different that that described in the homework statement has been solved. Here, the rotation rate of omega_OB is not constant, but instead, link OB is oscillating back and forth.
What you should sees from these animations is that the velocity of P as seen by a stationary observer is NOT tangent to the circular guide, whereas the velocity as seen by the observer on OB is tangent to the circular guide. Also, the observed acceleration of P always points to the inside of the circular guide, whereas the acceleration seen by a fixed observer does not always do so.
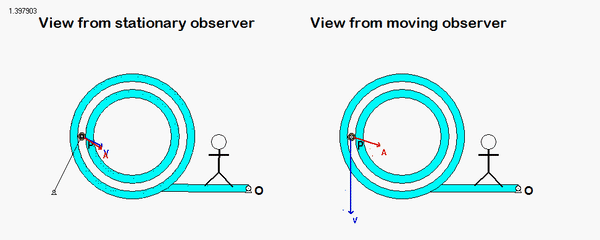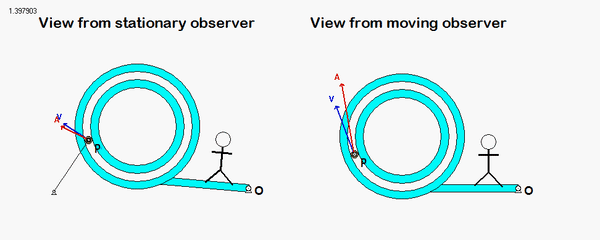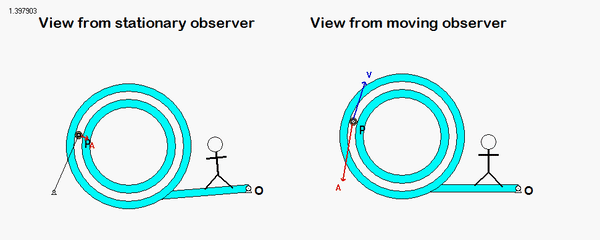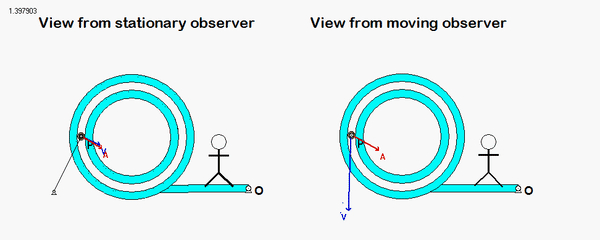
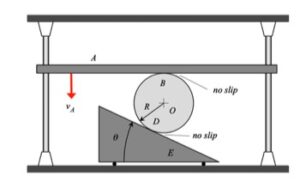
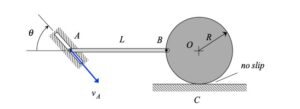
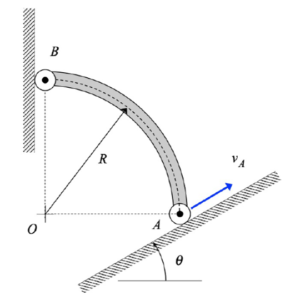
We need to treat this problem just as we have done for all planar mechanism kinematics in this course. For velocity analysis:
- Write down a rigid body kinematics equation relating points A and P. This vector equation will have one unknown: omega_AP.
- Write down a moving reference frame (MRF) equation kinematics equation relating points P and O. For this equation, it is recommended that you attach an observer onto link OB. This vector equation will have one unknown: v_rel (the velocity of P as seen by the observer on OB). Note that v_rel will be tangent to the circular guide.
- Set the above two velocity equations in terms of v_P equal, and balance coefficients of the xy unit vectors. This will give you two equations in terms of the two unknowns listed above.
For acceleration analysis, repeat the above steps using the rigid body acceleration and MRF acceleration equations. Note that for the MRF equation, the acceleration of P as seen by the observer will have TWO components: one tangent to the circular guide (the observed rate of change of speed, vdot_rel) and one perpendicular to the circular guide (the observed centripetal component of acceleration, v_rel^2/R). In the end, you will have two equations in terms of vdot_rel and alpha_AP.