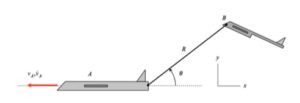
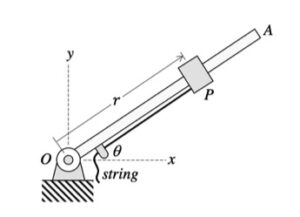
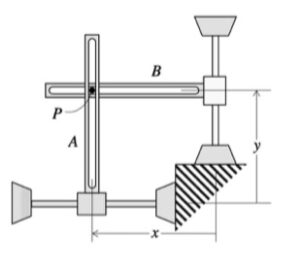
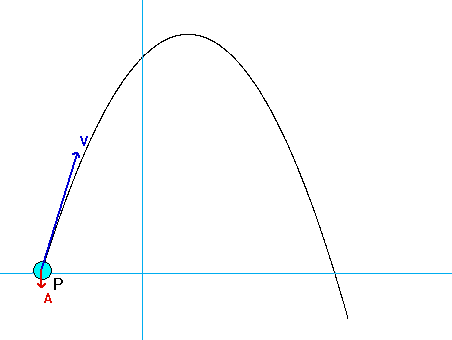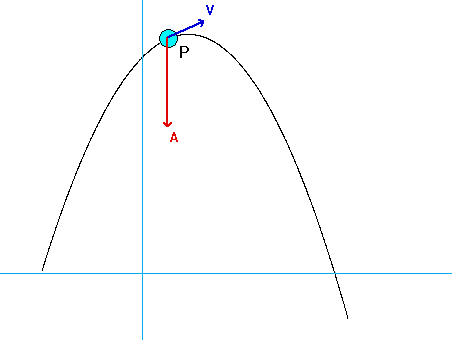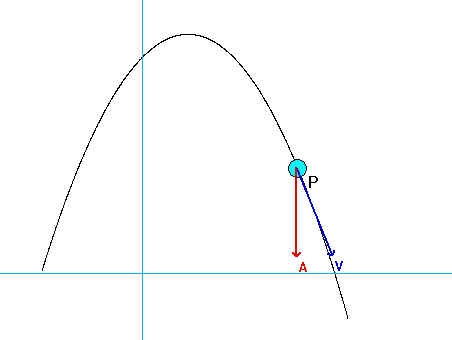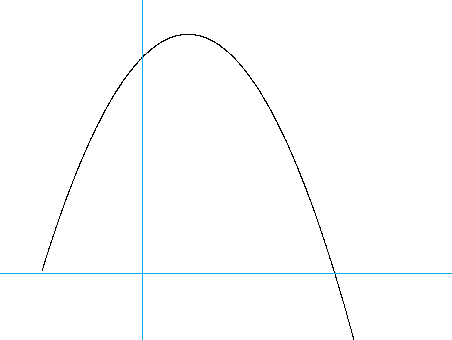
| Problem statement
|
DISCUSSION THREAD
Discussion and hints:
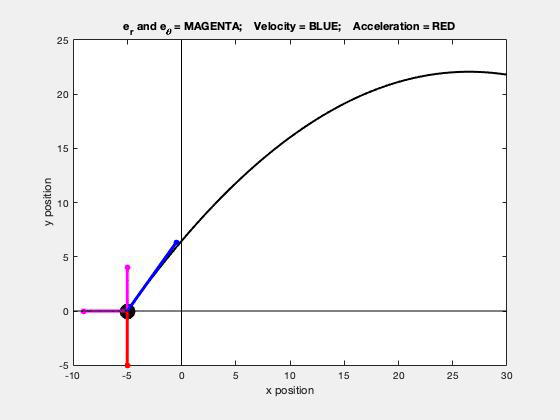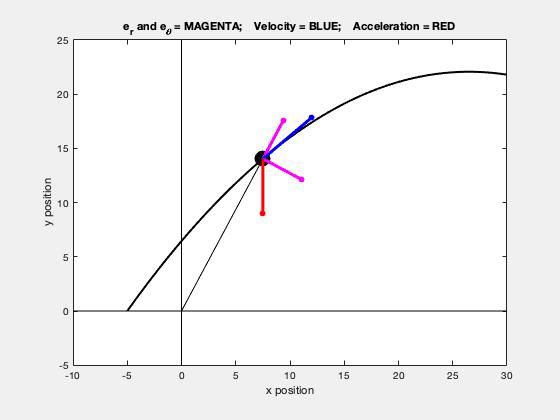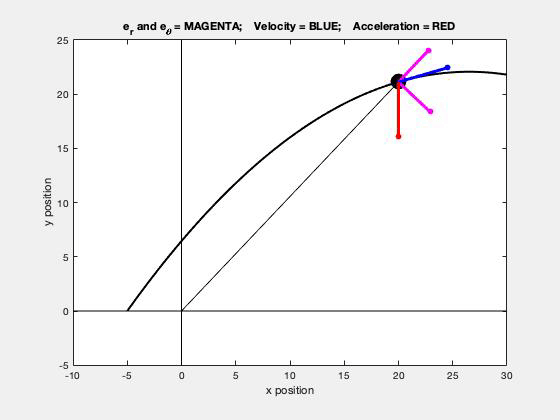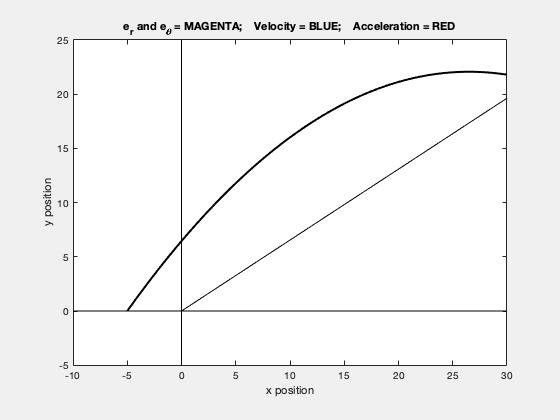
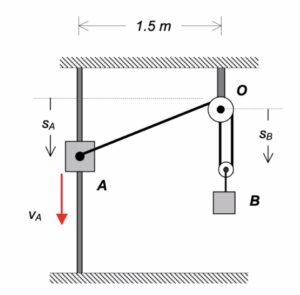
This is a typical cable-pulley problem for us in this course. Here, we need to first write the length of the cable, L, in terms of the position variables of sA and sB, along with some constants. Since it is assumed that the cable does not break, go slack or stretch, the length L is constant. Take a time derivative of the expression above for L. This relates the speeds of blocks A and B.
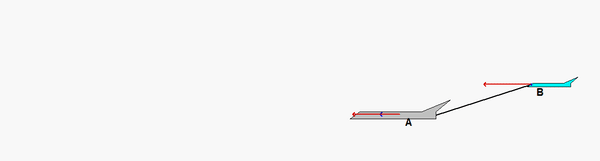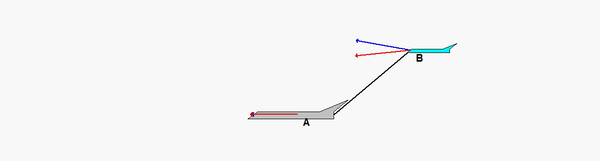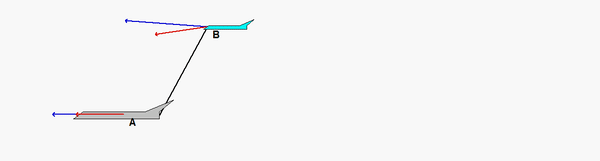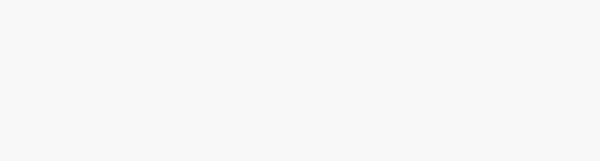
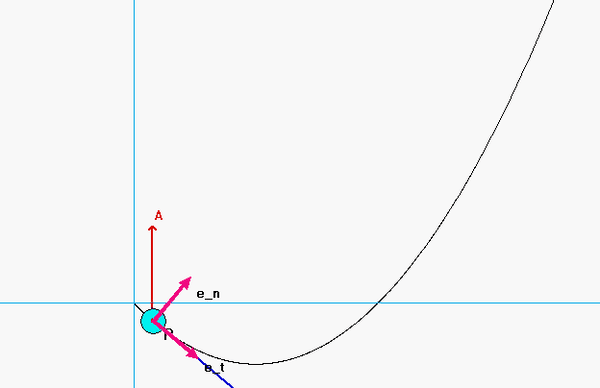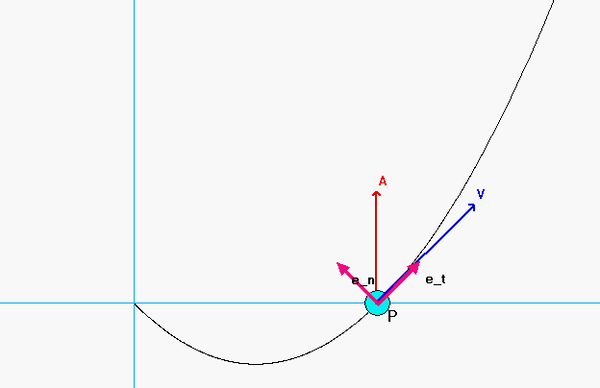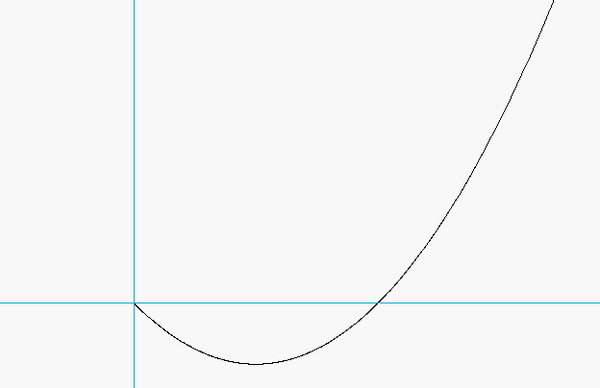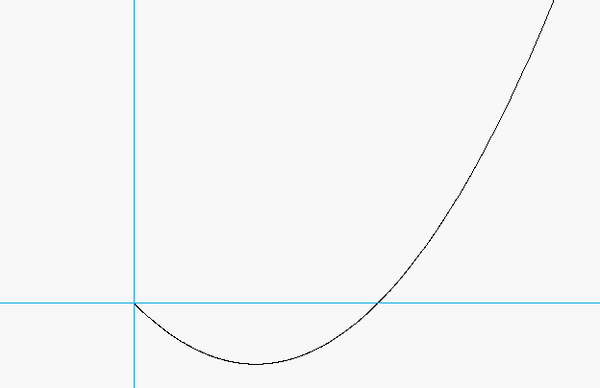
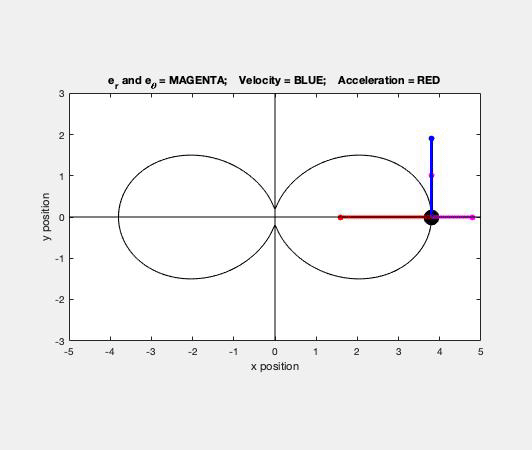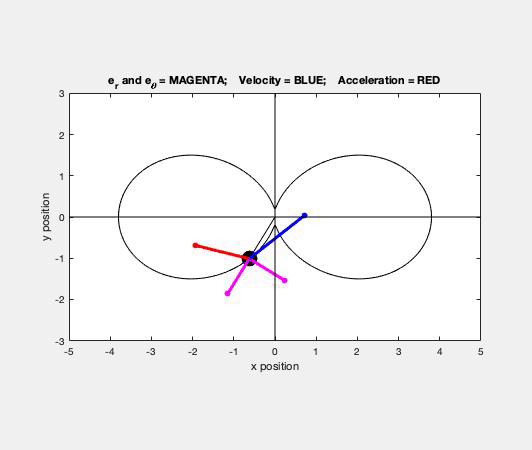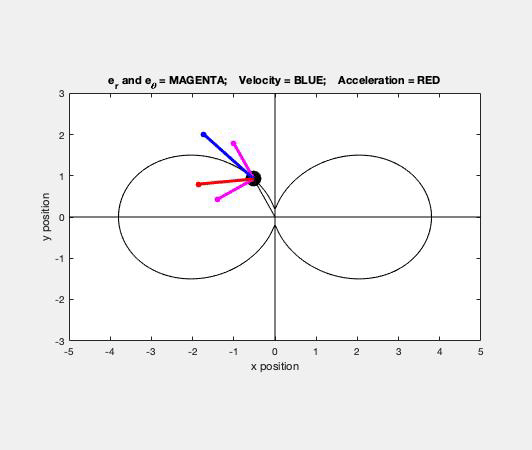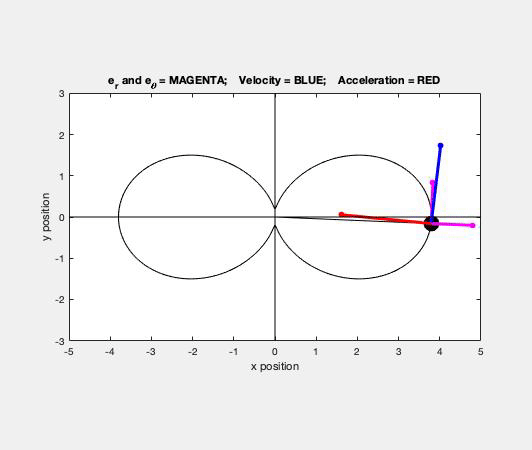
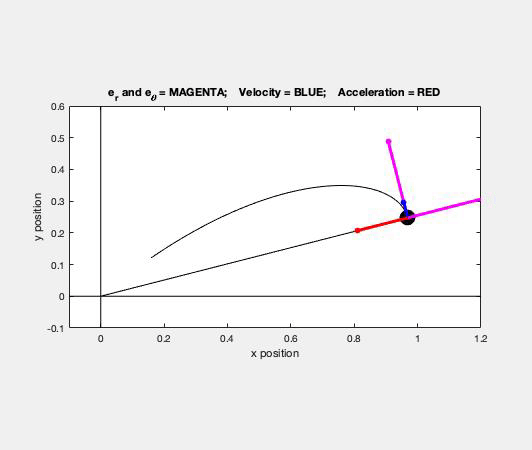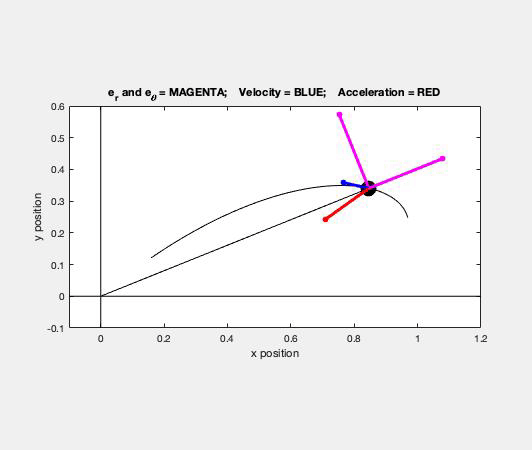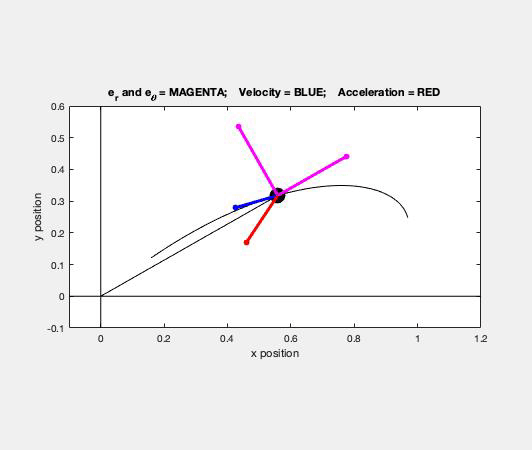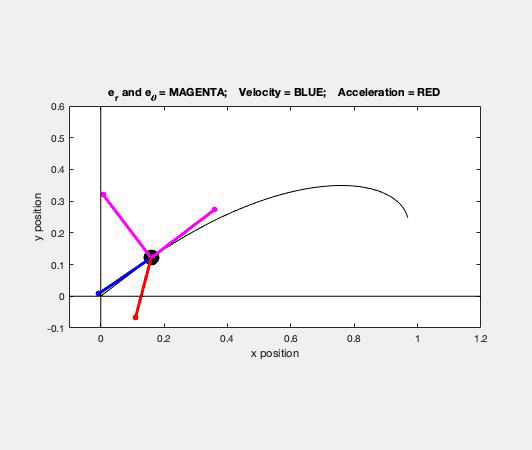
Carefully study the animation of the motion of this cable-pulley system provided below. One of the questions asked of you is the speed of B when sA = 0. What do you see in the animation below as sA passes through zero? Does your equation above tell you the same thing?
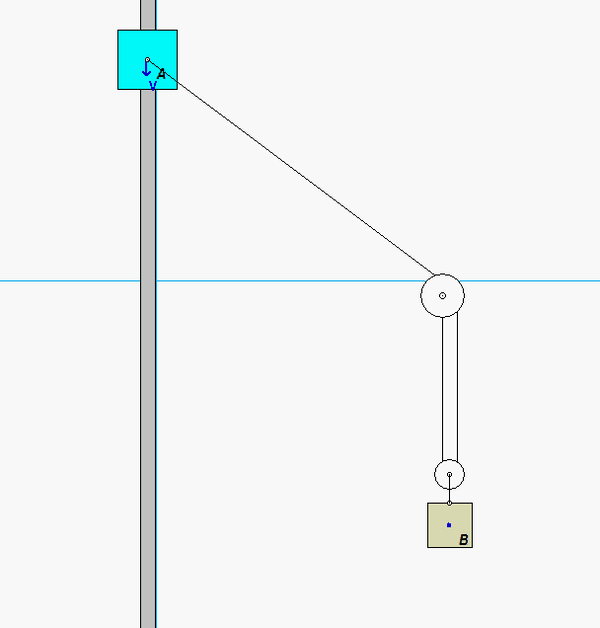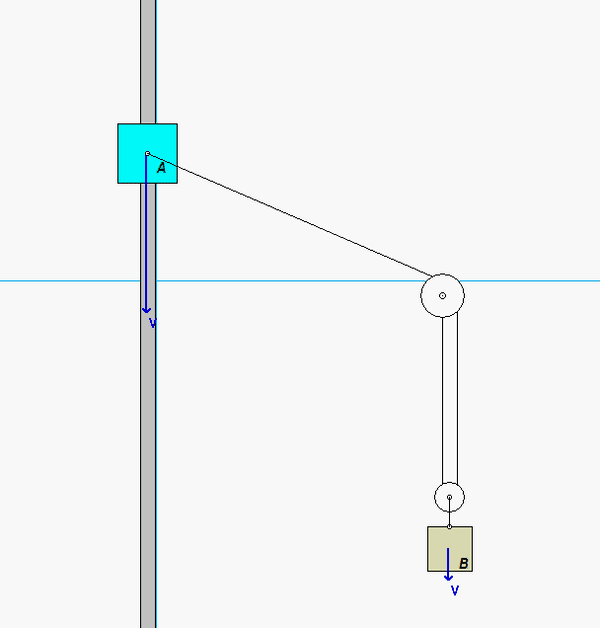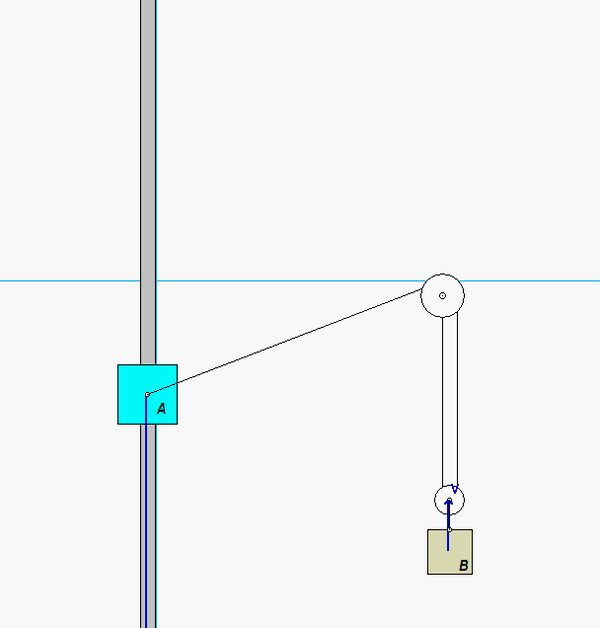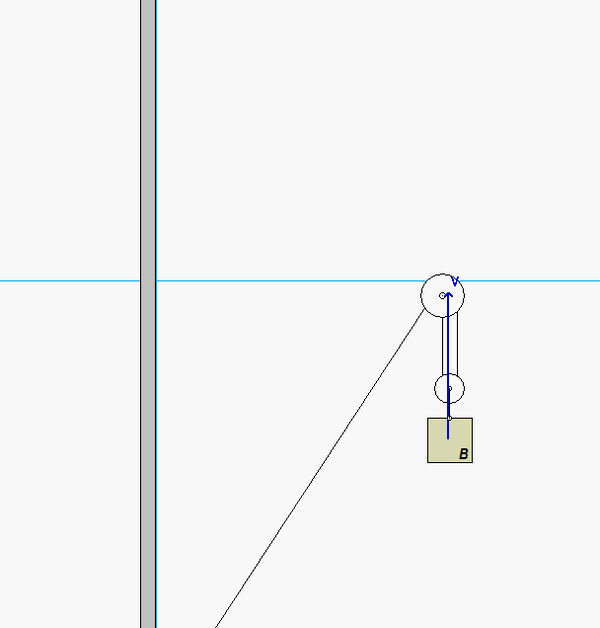
Any questions??