| Problem statement Solution video |
DISCUSSION THREAD
We encourage you to interact with your colleagues here in conversations about this homework problem.
| Problem statement Solution video |
DISCUSSION THREAD


We encourage you to interact with your colleagues here in conversations about this homework problem.
| Problem statement Solution video |
DISCUSSION THREAD

Discussion and hints:
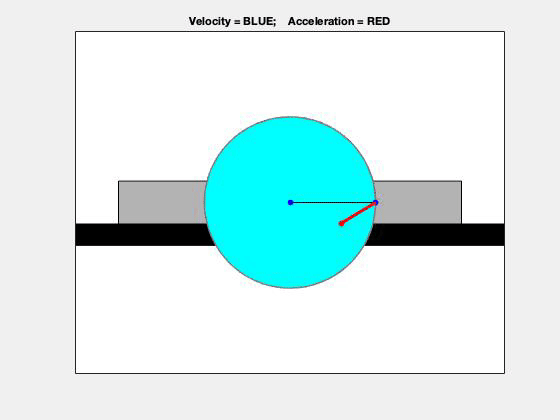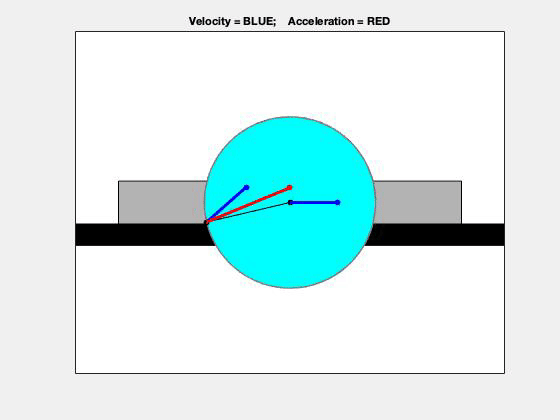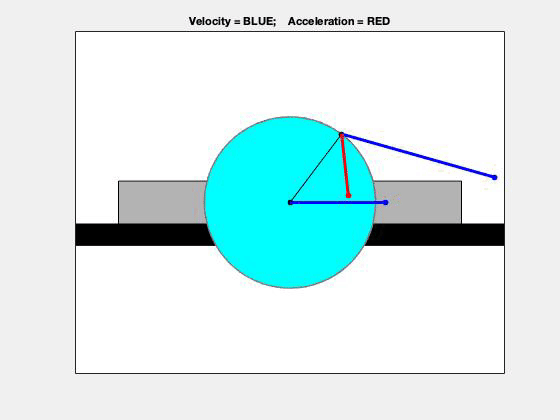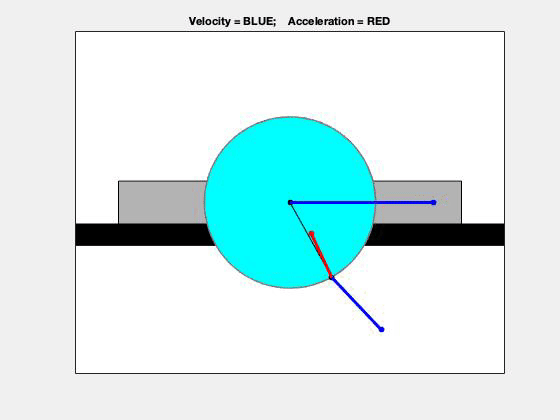
Note that since the top contact point of the disk rolls without slipping on the upper fixed surface, this contact point has zero velocity. In addition, the horizontal component of acceleration of that point is also zero (the vertical component of acceleration is NOT zero, however).
For the velocity problem, write down the velocity kinematics equation for the disk (where “C” is the contact point):
vO = vC + ω x rO/C = ω x rO/C
and solve for the angular velocity of the disk. For the acceleration problem, write down the acceleration kinematics equation for the disk:
aO = aC + α x rO/C – ω2rO/C = aC j + α x rO/C – ω2rO/C
and solve for the angular acceleration of the disk.
Then, write down and use the acceleration rigid body kinematics equation relating points O and B.
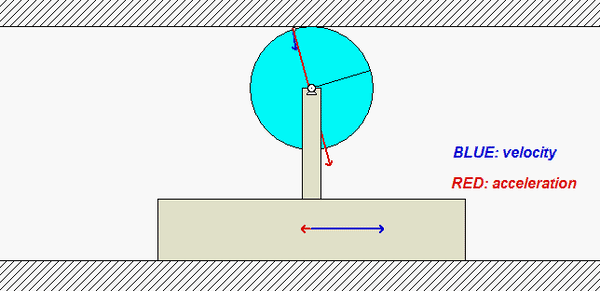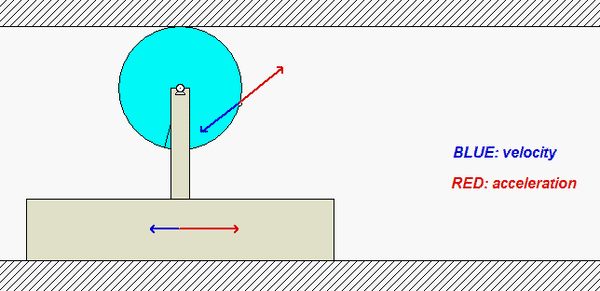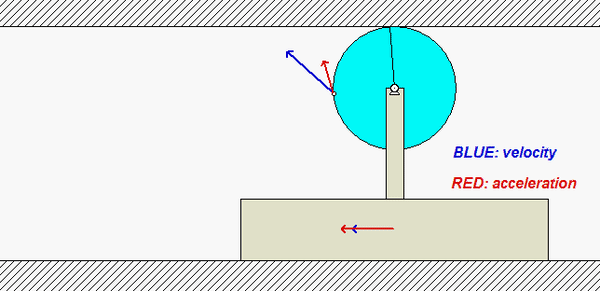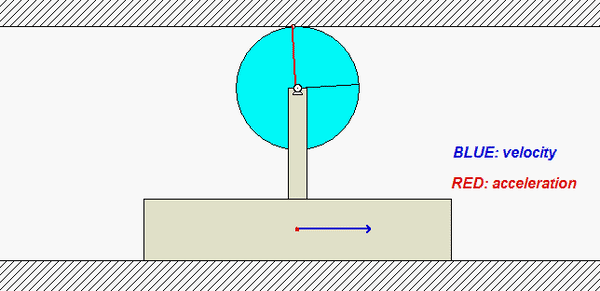
Carefully study the velocity (BLUE) and acceleration (RED) information for the point on the circumference of the disk shown in the animation below. Recall that the velocity of the point on the disk in contact with the fixed upper surface is zero, and its acceleration has only a vertical component. Do you see this in the animation?
Any questions??
| Problem statement Solution video |
DISCUSSION THREAD
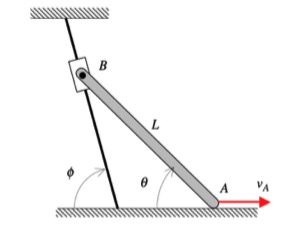
Ask your questions here. And, consider answering questions of your colleagues here. Either way, you can learn.
DISCUSSION and HINTS
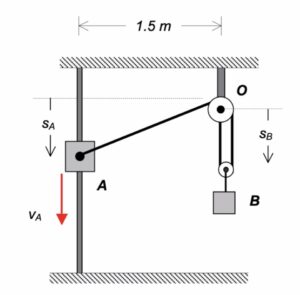
In this problem, end A of the bar is constrained to move along a straight horizontal path with a constant speed of vA, whereas end B is constrained to move along a straight, angled path. As you can see in the animation below of the motion of the bar, the speed of B is NOT a constant (the acceleration of B is non-zero, and is, in fact, increasing as B moves along its path).
In your solution, it is recommended that you use the rigid body kinematics equations relating the motion of ends A and B:
vB = vA + ω x rB/A
aB = aA + α x rB/A – ω2rB/A
For these equations, you know: i) the magnitude and direction for the velocity of A; ii) that the acceleration of A is zero (constant speed along a straight path); and, iii) the direction for the velocity and acceleration of B. These two vector equations produce four scalar equations that can be solved for four scalar unknowns: vB, aB, ω and α.
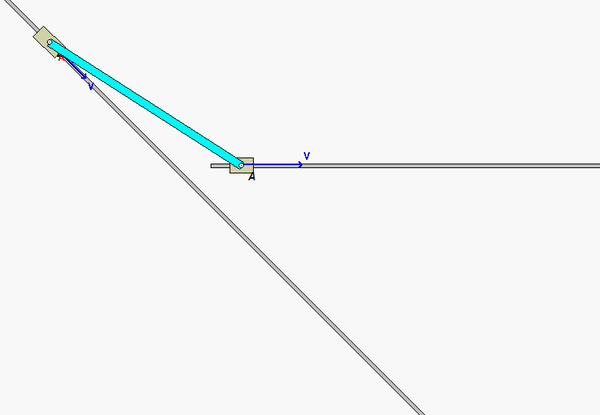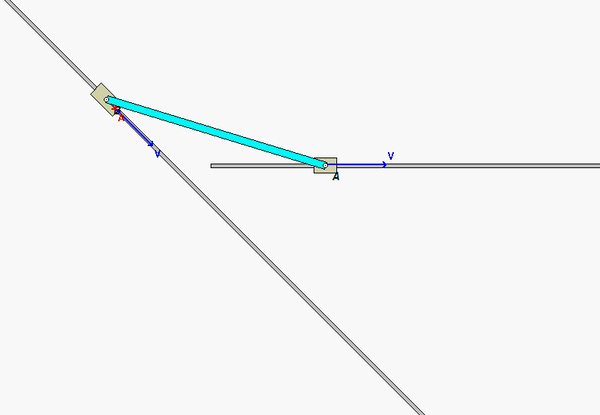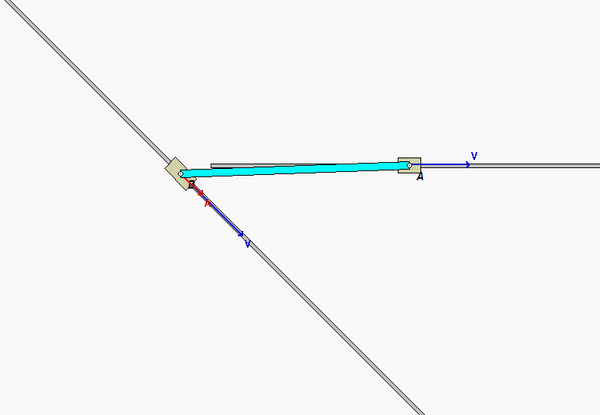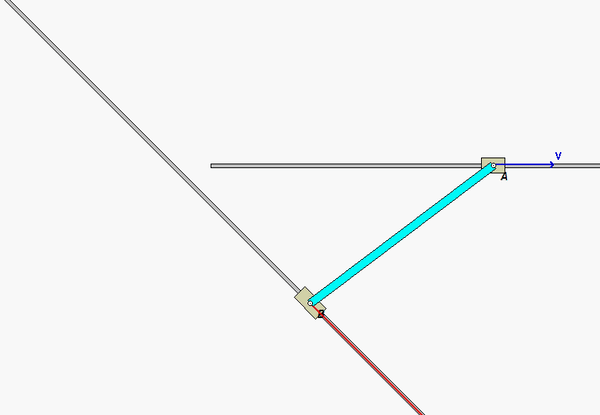
| Problem statement Solution video |
Note: Due to the weather-related changes in the course this week, this problem will NOT be collected.
DISCUSSION THREAD
Discussion and hints:
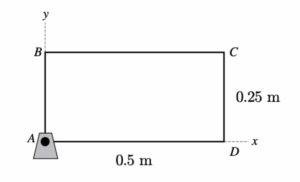
The solution for this problem requires only a straight-forward application of the rigid body acceleration equation, relating the known accelerations of points A and C:
aC = aA + α x rC/A – ω2rC/A
Since this vector equation has two components (x and y), you have two scalar equations from which you can solve for ω and α.
Any questions??
| Problem statement Solution video |
Note: Due to the weather-related changes in the course this week, the submission of this problem can be delayed until 11:59PM on Friday, January 30.
DISCUSSION THREAD
We encourage you to interact with your colleagues here in conversations about this homework problem.
Discussion and hints:

Enlarged view
This problem is a straight-forward application of the planar rigid body kinematics equations. The velocity and acceleration of the center of the disk are known, as well as the angular velocity and angular acceleration of this disk. To find the velocity and acceleration of point A on the disk, you can use the following:
v_A = v_O + omega x r_A/O
a_A = a_O + alpha x r_A/O – omega^2*r_A/O
Using the enlarged view above, we can see the interplay between velocity (blue) and acceleration (red) of point A. Using what we learned back in Chapter 1, can you identify times when the speed of A is increasing and when it is decreasing? (Hint: Look at the angle between the velocity and acceleration vectors.) Using the top view, we can see the path of point A – is that the path that you expected for A?
| Problem statement Solution video |
DISCUSSION THREAD
Discussion and hints:
This is a typical cable-pulley problem for us in this course. Here, we need to first write the length of the cable, L, in terms of the position variables of sA and sB, along with some constants. Since it is assumed that the cable does not break, go slack or stretch, the length L is constant. Take a time derivative of the expression above for L. This relates the speeds of blocks A and B.
Carefully study the animation of the motion of this cable-pulley system provided below. One of the questions asked of you is the speed of B when sA = 0. What do you see in the animation below as sA passes through zero? Does your equation above tell you the same thing?
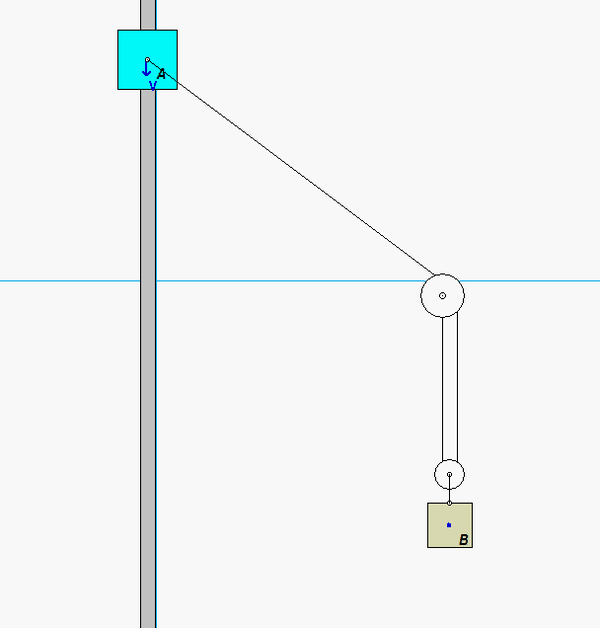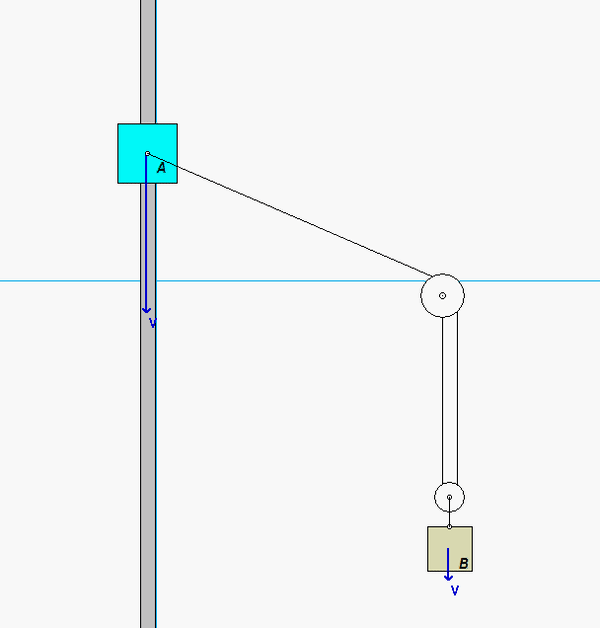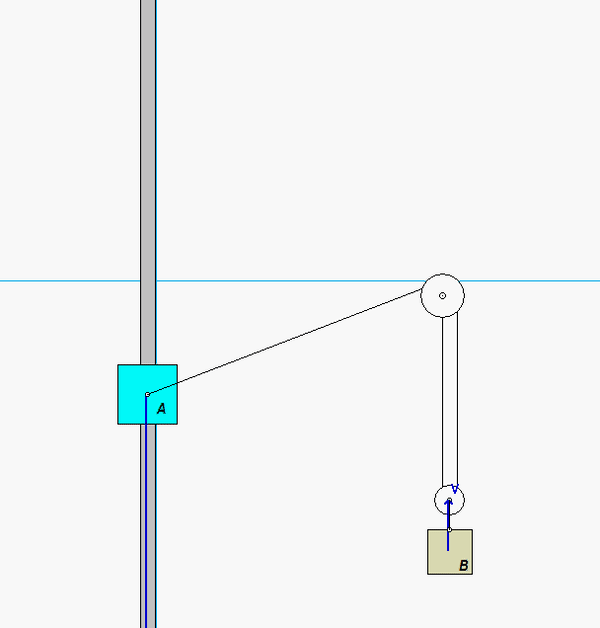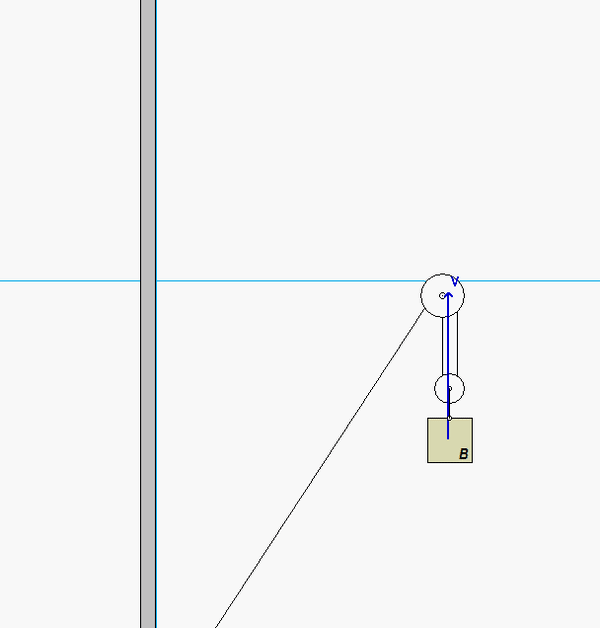
Any questions??
| Problem statement Solution video |
DISCUSSION THREAD
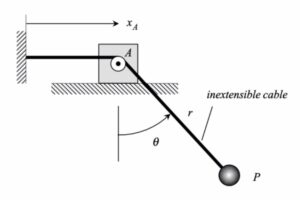
Discussion and hints:

An observer riding along on block A will describe the motion of P relative to themself in terms of the radial distance r and the cable angle θ. Because of this, it is convenient to use the relative motion kinematics equations to write down the velocity and acceleration of particle P: vP = vA + vP/A and aP = aA + aP/A , where the relative velocity and relative acceleration terms are written in polar form:
vP/A = r_dot er + r*theta_dot eθ
aP/A = (r_ddot -r*theta_dot2) er + (r*theta_ddot + 2r_dot*theta_dot) eθ
You will need to write the polar unit vectors er and eθ in terms of the Cartesian unit vectors, i and j, at some point before you can add together terms.
QUESTION: What is the relationship between xA and r? (Recall that the cable remains taut at all times.)
An animation showing the path of point P corresponding to θ_dot = constant is provided below. How does this true path differ from the view of the path as seen by the observer on A? Can you visualize that? HINT: The path seen by the observer on A is an inward spiral centered on the observer (point A).
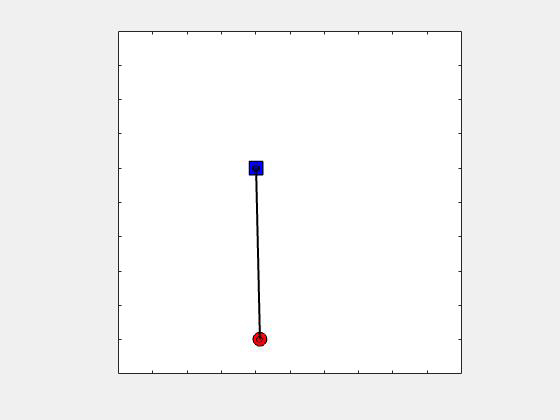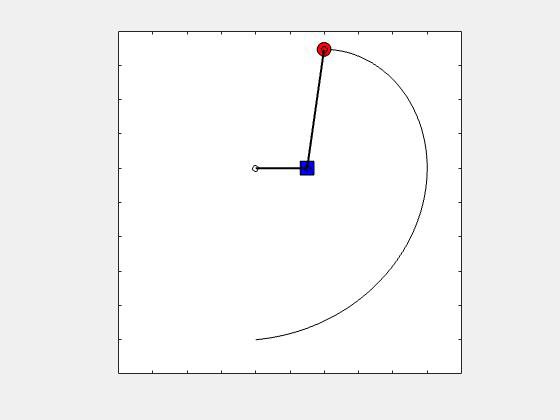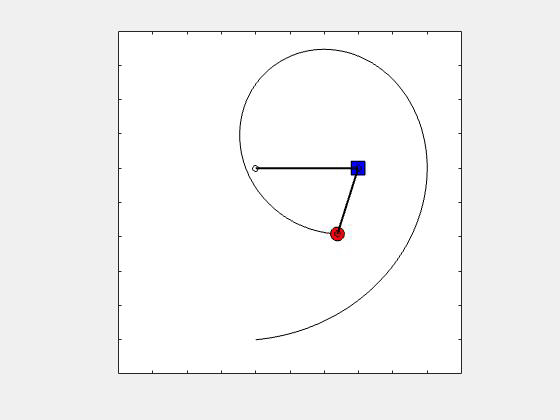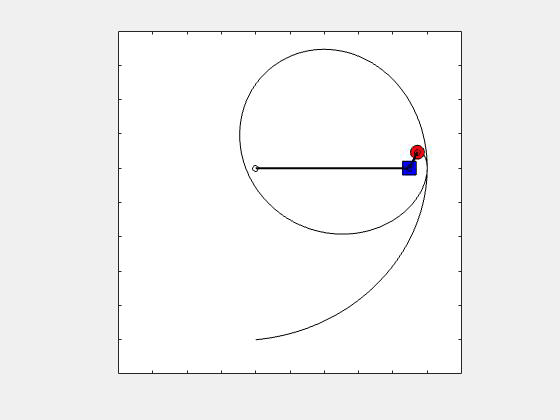
Any questions??