| Problem statement Solution video |
DISCUSSION THREAD
Discussion and hints:
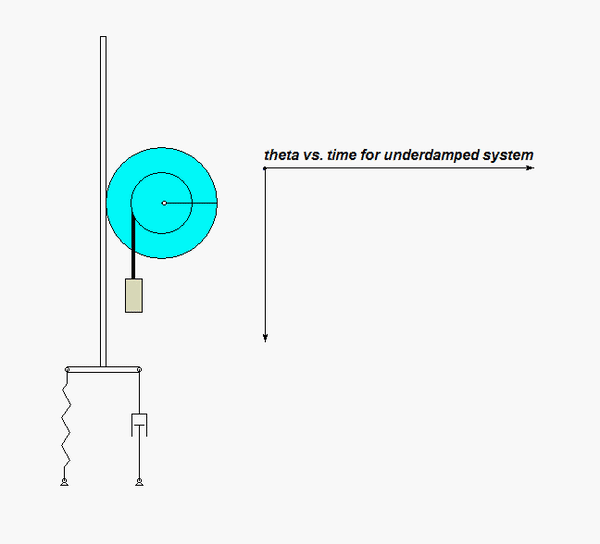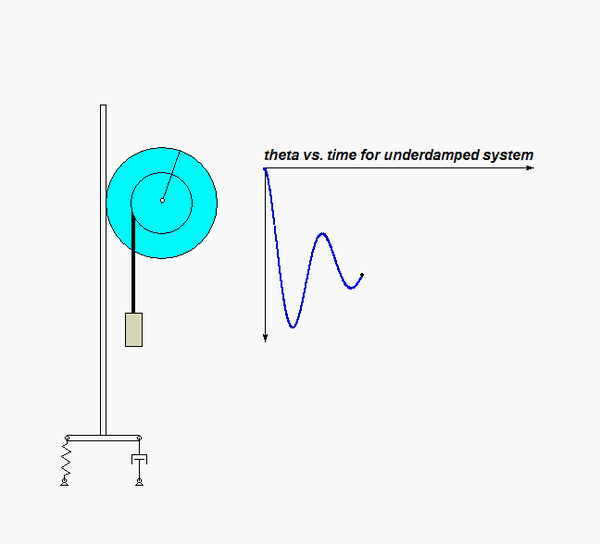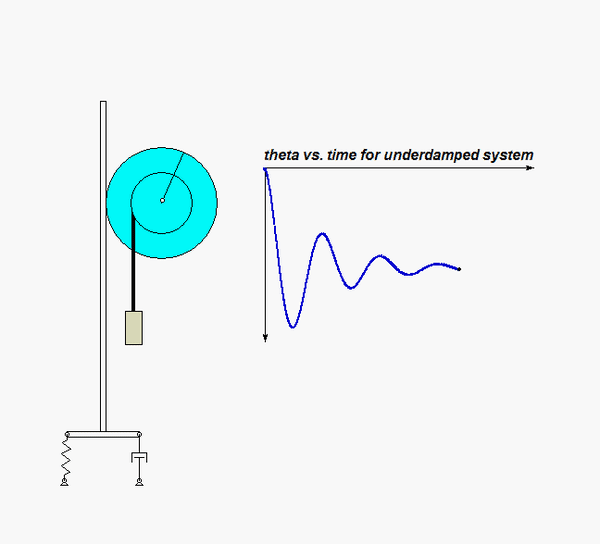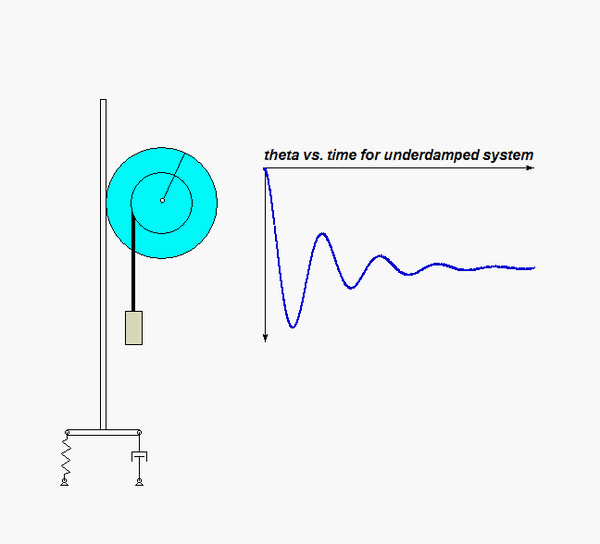
Shown below is an animation of the results of a simulation of the motion corresponding to an UNDERDAMPED system. The response is oscillatory, however, the amplitude of the response decays away at an exponential rate.
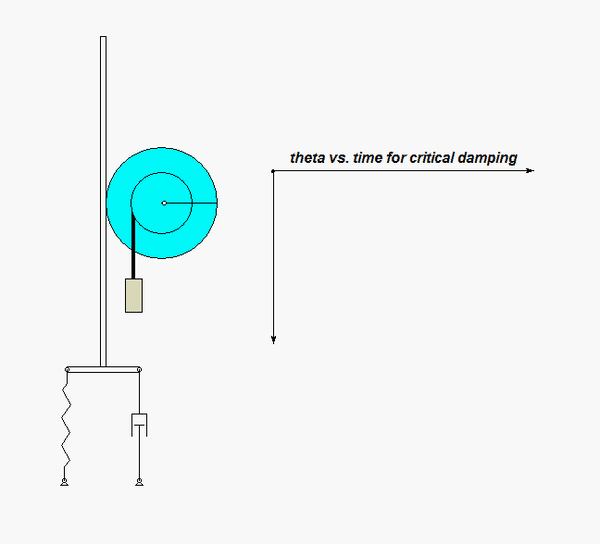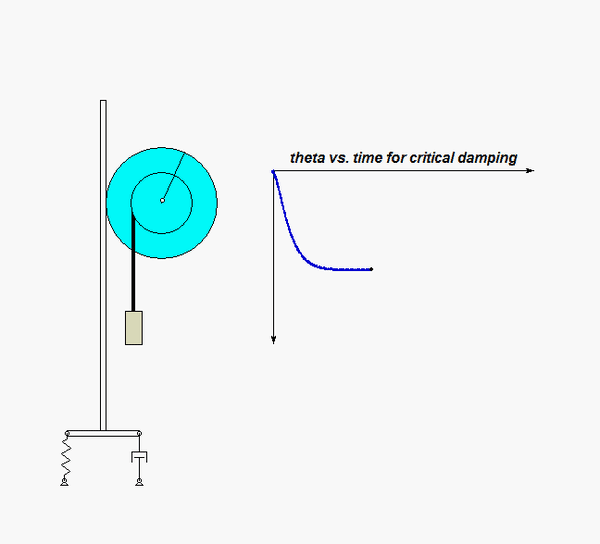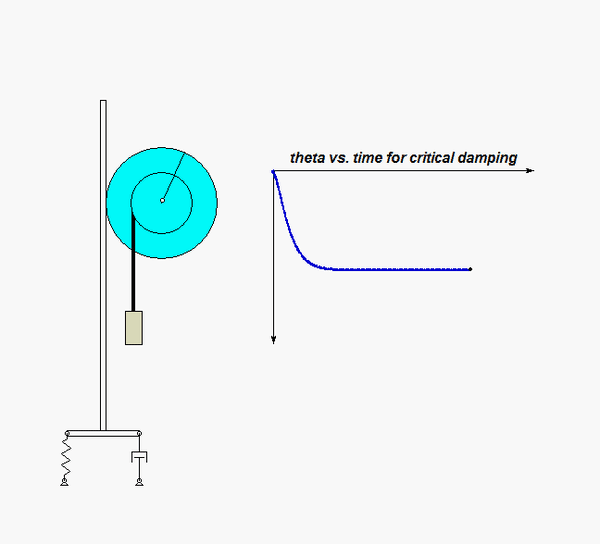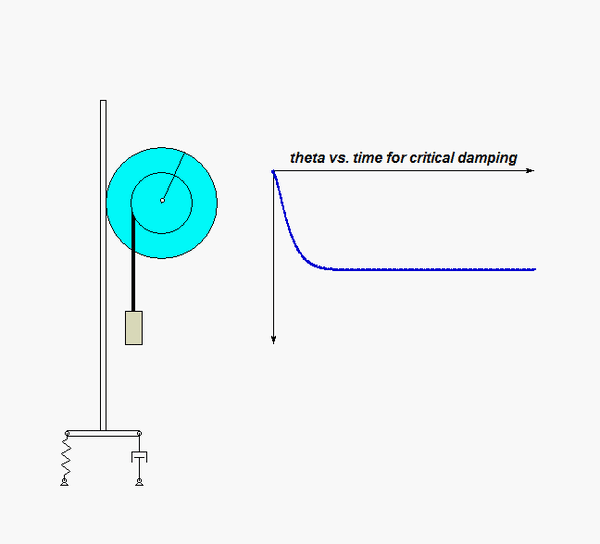
For this problem, you are asked to determine the amount of damping (i.e., the value of c) for which the system is CRITICALLY damped (ζ = 1). The animation below shows the response of such a critically damped system. Not that with this value for the damping ratio ζ, the oscillations are damped out, with the response asymptotically approaching the steady-state static equilibrium state.
The derivation of the dynamical equation of motion (EOM) for a system is a straight-forward application of what we have learned from Chapter 5 in using the Newton-Euler equations. The goal in deriving the EOM is to end up with a single differential equation in terms of a single dependent variable that describes the motion of the system. Here in this problem, we want our EOM to be in terms of θ(t).
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
Draw individual FBDs of the drum and the bar. Define a translation coordinate, x, for the bar.
Step 2: Kinetics (Newton/Euler)
Write down the Newton/Euler equations for the drum and the bar.
Step 3: Kinematics
Use the no-slip condition between the drum and the bar to relate x to θ.
Step 4: EOM
Combine your Newton/Euler equations along with your kinematics to arrive at a single differential equation in terms of the dependent variable θ.
You will then need to find the static rotation of the disk from your EOM. Also, put the EOM in "standard form" in order to find the undamped natural frequency ωn and the damping ratio ζ of terms of the given parameters for the system. Critical damping corresponds to ζ = 1.
Any questions?
Taking the moment about the center of the drum would mean that the moment equation would only have the effect of the spring, dashpot, and the weight of the particle. Remember that the radius of gyration replaces the I_o term with m*k_o^2.
Thanks! I was confused about whether to use the k term there or if could just do mass and radius.
Do we follow the the FBD on freeform that have the smooth rollers over the one on the problem statment that is just a cable floating?
They are kinematically equivalent.
Can I say the movement of the bar is the movement of mass A times 2? Because of the double radius.
Yes. Remember velocity is equal to the radius times the angular velocity. Since the drum is rotating with angular velocity theta, both components rotate with the drum. So, just the radius will differentiate the two. The movement of the mass will be represented by thetaR, while the movement of the bar will be represented by 2thetaR.
Does the "tension" of the cable that is attached to the spring and dashpot act in the upwards or downwards direction on the drum?
I used that they acted downwards on the drum. Since the positive x direction of movement is upwards, this would insinuate that these components are stretched and therefore pulling down on the drum. Having them in the opposite direction will also help all of the signs in your final EOM equation match.
Since connector B has no mass can we say that its acceleration is 0?
From Newton: the summation of forces on a particle is equal to mass*acceleration. If mass = 0, then mass*acceleration = 0.
You can ignore B in the problem because the mass is negligible. It is almost like the spring and dashpot forces are pulling directly on the cable connecting B to the drum.
having a mass of 0 does not mean you will have an acceleration of 0 . however that in fact mean that you will have a sum of forces of 0 according to Newton's law
I made this mistake the first time when constructing my kinetic equations. Professor Krousgrill's response to a similar point made above elaborates a bit on this.
To find the tension force connected to the inner drum and particle A, do we need to take into account the acceleration of A as well or do we say that the tension in this cable is just equal to the gravitational force produced by the particle's mass?
Since the mass of bar B is negligible, what do I equate the sum of forces in x direction of bar B to? Would the sum of forces be equal to 0 in x (x direction is vertical)?
Yes you would equate the forces of bar B to 0 because the mass is negligible. This will allow you to have find a relationship between the forces due to the spring and dashpot and the tension force from the bar.
Yes. Since the mass is negligible, 0xa will be zero.
Remember that the angular speed for the outer and inner disks are different, so you will need to relate the two using the displacement of A and B. By relating these two, you can solve for your EOM.
The inner and outer disks of the drum form a single rigid body. The angular velocities of the two portions of the drum are the same.
Professor Krousgrill,
Are there any cases in which the inner and outer disks cannot be treated as a single rigid body?
a good trick here is to take the moment across the center of the disk so that you do not need to worry about any other forces other than the spring and the dashpot and the mass
Another benefit of taking the moment across the center of the disk as opposed to a contact point would be that it allows you to incorporate friction so you can relate x and theta. If you had taken the moment about a contact point, you couldn't use the "no slip" condition since the force goes through the point you're using
I am a little confused as to how to determine the direction of the force due to the dashpot. Does anyone have tips that they use to determine the direction when solving various problems?
What helped me the most is to reference the directions of motion, both theta and x, and determine the resultant forces on the object from springs and dashpots and how they would both act against directions of motion. The spring is more intuitive because the spring is either in tension or compression and the forces are the results of that motion, k*x. Dashpots dampen the motion, usually by flowing fluid, so it acts against the assumed x at a rate of c * x(dot).
The way I think about it is that for springs and dash pots they always exert a force to oppose movement of the object they are attached to so if ur body is moving right and it has a dash pot attached to it at the sides the dash pot applies a force to the left, regardless if the dash pot is on the right or left of the object moving
Even though after release the drum will clearly move counterclockwise can we assume initial movement in the positive direction to draw our FBD just for convenience of equations? Or do we have to assume initial direction logically?
Recall that the purpose of the dashpot is to dampen/resist motion, so it will act against the x value. For me, drawing the directions of all of the forces and then adding cx(dot) at the end helps me understand the dampening direction.
I find it best to think about the direction of acceleration the dashpot would cause. That is the direction of the force, which would always be in the opposite direction of the velocity.
When relating the forces from the spring , dashpot, and block A, it is important to recognize they are about two different radii when relating x' to θ' and x'' to θ''. The spring and dashpot are about a radius of 2R while block A is about a radius R.
To avoid this confusion I chose to use the variable x for the spring and dashpot, and the variable y for block A.
It is critical to define your positive directions for the respective axis and then follow that throughout the entire problem
If theta_+ is in the clockwise direction, does that mean we have to flip the sign of the moments in the Euler equation?
If theta is defined positive in the CW direction, then a moment in the CW direction would also be positive.
If theta is defined positive in the CCW direction , then a moment in the CCW direction would also be positive.
It is important to remember for part c that when you take the 1st and second derivative of z theta static is zero
Why is there something called theta positive clockwise rotation when we usually define rotation in the clockwise direction as negative and the counterclockwise direction as positive?
When you say that we "usually" consider CCW rotations to be positive, you are assuming that the coordinate system has x positive to the right and y positive up - then by the right hand rule, the rotation about the z-axis is positive in the CCW sense.
In vibrations, we typically have a number of moving parts, with coordinates needing to be defined for each one. We may find it to be more convenient to define an x axis as being positive to the left, or even along some angled incline. We do not want to be bound to having x positive to the right. That is why we will define our positive sign conventions in ways that are most convenient, and be sure that we stick by these conventions all through the four steps of the solving process.
Oh ok, that makes sense. We can just define the x sign direction in a way that makes it the easiest and then define the rotations in relation to the sign definition we chose.
What is the easiest definition to use for this whole problem? Is it easy to stick with the positive CW definition or changing it to negative CW would be easier? I always struggle to understand that difference in positive and negative.
Those choices are totally up to you. If you want to stick with theta always being positive in the CCW sense, then do so. It is your choice.
I see similar to the answer you gave up above about me asking for the CW positive. Its the way I choose to define it for the CW and CCW signs.
On the example diagram, it says to show individual body diagrams for the drum and block- since the cable is now replacing the block so we just show its effect on the drum fbd instead of drawing a separate fbd for the cable and spring/dashpot?
I found that the approach to this problem was similar to that of H6D
I also found this homework problem similar in concept to C6.4 (the conceptual problem hints helped a lot!)
The way that I found to best approach this problem is to leave the orientation of positive theta in the clockwise direction and have the force of the dashpot and spring going down off of the left edge of the disk. I also found that it was useful to draw the free body diagram of just block A to find the equation for tension.
For the Find part E, are we supposed to find a number for C K and M, or simply set the equation of the damping ratio equal to 1 and plug in our values for C, K, and M
Is the part e formula supposed to be the damping ratio? On the paper it is C/(KM)^1/2, but the dampening ratio is C/(2(KM)^1/2)
Part e is not supposed to be the damping ratio. The 2 in the denominator cancels nicely to create an answer for C/ sqrt(KM)
I found E.B.5 to be helpful to understand the concept more on this problem.
Make sure to solve for theta_st by relating all the derivatives to 0. From this, solve for theta and set this equation into the original to get the answer in terms of z.
Given that this problem uses a mass connected by a string to a pulley, is it correct that we cannot say the sum of forces on block A is equal to zero? Block A definitely has a mass and then may also potentially have an acceleration, correct?
I believe this is not true. Because of the fact that A can accelerate the force cannot be assumed to be zero.
A vital part in solving this problem is to correctly relate the tension of the cable with the disk it is acting on, this is a mistake I made when solving this problem. Additionally, remember to relate the spring with the disk in terms of K.
Are we just supposed to assume that the cable can pull downward and is stiff enough to push upward?
Yes, follow the figure shown here on this post, where the cable is actually a rigid body that can handle both tension and compression.
Does the dash pot just act always in a direction opposite to the force of the spring?
Follow your sign conventions in order to determine the direction of the dashpot force. As examples:
• If you define x and x_dot to be positive to the RIGHT, then with motion in the positive direction (to the right) the dashpot will exert a resisting force, that is, to the LEFT.
• If you define x and x_dot to be positive to the LEFT, then with motion in the positive direction (to the left) the dashpot will exert a resisting force, that is, to the RIGHT.
These same observations hold true for springs, except there you consider the position rather than the motion.
If a dashpot velocity is x_dot and a spring stretch/compression is x, then the dashpot force and spring force will be pointing in the same direction, not opposite to each other.
I found example 6.B.5 helpful when solving this problem. From the sum of the forces on the block, you can solve for the tension value. Then this value can be plugged into the moment of the drum to find the EOM.
A few notes from my solving of the problem:
1. Remember that if something has no mass, then it has no acceleration.
2. Remember that both tensions have different radii, meaning that they will always be a magnitude difference.
3. For finding the ratio of parameters, factor out k_o as many times as you can until you get the ratio. Your final answer should be in the form c/sqrt(km).
When solving this question, make sure to make a FBD and a summation of forces for the block A. This is because the block has a tension force and therefore the extra equation is necessary to solve each variable.
Yes I completely agree. Without the FBD you cannot solve for the missing tension force.
In this question what direction would the friction be acting?
The diagram on the pdf and the diagram from the discussion thread are slightly different. What helped me was looking at both of them- but specifically understanding that the bar to draw the FBD of is the vertical bar in the discussion thread and not B from the PDF.
In regard to theta+ does it matter that it is positive in the CW direction instead of the usual rule that CCW is positive? Would we need to flip this, or will it have no effect in the long run?
As long as you keep your signs consistent the directions can be whatever you deem to be easiest.
Don't forget to include friction when taking the moment about the center of the disk. This allows you to get x and theta in a common equation.
For this question, it is very useful to remember your relationship between x and theta. One mistake I made while doing this problem is that I forgot to account for the outer radius being twice as large when doing this. Also, for part e of this question, it is important to make note of what you're given. Critically damped means that the damping ratio is equal to 1. Were also given R/Ko = 1, which means that R=Ko. Using this information, you can solve for c/sqrt(KM).
Comments are saying to include friction. Is there no friction in the pdf hw (and not the comment hints version)?
The two models are identical in terms of the rotation of the disk. In my opinion, the figure with the cable in the PDF is easier to consider as there are less forces.
I understand how to substitute Z in for X to get rid of the right side of the equation. However I don’t quite understand how that works conceptually. Does anyone have a good explanation as to why this works?
When solving for kinetics, there is no Fx making your main equations Fy in the cable and drum along with the Moment. These can then be plugged into the kinematics, which is initially at rest.
Would it be helpful to make multiple FBDs for this problem? Would a separate FBD needed for B?
No, you only need one FBD of the Drum, then sum the moments about the center of the drum to get the EOM
The connector would still produce a force correct?
Drawing individual free-body diagrams of the wheel, A, and B with the x-components acting on them, and then converting the x to theta components is a good starting point.
For this question, I drew free body diagrams for the drum, block, and mass A. I then took the moment about the center point of the drum and used Newton equations for the block and mass A and substituted that information into the moment equation from before. This helped me derive the equation on motion. I believe to determine the static rotation of the drum you have to set theta dot and theta double dot equal to zero and solve for theta.
Wouldn't you only need to set theta double dot to zero? Because Static Equilibrium requires a netforce of zero (meaning no acceleration).
For this problem it is important to note that B does not have a mass. From here you can make a critical relationship between the outer tension, the spring force, and the Damping force. It may also be helpful to create an FBD of A to solve for inner tension. From there, the variables are known and the EOM can be created.
For this problem, can we assume that the spring is unstretched when theta = 0?
In order to write the EOM in terms of theta, remember to substitute x with (R)(theta). The derivative of this can be used for x_dot and x_ddot
In order to derive the equation of motion, it helps to draw out free body diagrams to substitute the tension values created by the two cables with the needed spring and dashpot values to finally obtain the correct answer in terms of the coordinate θ.
For the last part of the problem, the ratio of R and kO being equal to one means the two values are equal to each other. This helps out the math when determining the ratio of parameters because either value can be substituted for each, and, therefore, simplifies the math and makes it easier to get to the final answer.
Assume the normally positive y-axis is the positive x-axis. This will allow you to use the characteristic equation without issue for the EOM.
Some helpful tips for solving this problem: b does not have mass, assume the normally pos x and y axis, substitute x with r theta and take the derivatives from there.
Does R/ko = 1 apply to the whole problem or just part e?
I started with a moment equation around the center of the disk. Since there is no mass, a simple summation of forces on point B allows for you to solve for the tension force on B.
In order to relate x+ and theta+, I used the velocity equation between the center of the disk and the contact point of the cable on the outer radius. This is similar to using the contact point of a rolling circle with no slip conditions like in previous homework problems.
For the last part of the problem, keep in mind the relationship between R and k_o, as this will help simplify the calculations into the variables specified (c,k and m). Additonally, consult page 388 of the lecturebook for what value should of zeta implies critical damping.
When drawing the FBD, is the direction of the friction in regards to the dashpot the same as with the spring. That is, do dashpots behave the same as springs friction-wise?
Are we supposed to use the new formula with forced response or still the free response?
Remember that the force contribution from the dashpot will oppose motion, so be consistent after defining the translation coordinate for the bar. Additionally homework H.6.D is helpful to consult for part c.
When finding the ratio of parameters, using the equation that relates the damping ratio, the natural frequency and C is important. It is important to note that C in this case is the coefficient of x dot in the EOM. This equation should simplify greatly with the relation given in the problem and the fact that zeta = 1 in for critical damping.
Is it also possible to solve this problem by taking the moment about the edge where the cable is attached to B and the disk and the moment about the edge where the cable is attached to A and the disk, or should the moment only be taken about the center?
The only non-accelerating point on the disk is its center (which is also the center of mass). Therefore the only candidate for the moment equation is the center of the disk.
To solve this problem, it is best to start with the FBDs of the drum and bar, then connect their Newton/Euler equations using the tension in the cable connected to the bar. Next, a translation of x to theta is needed to write the ODE in terms of theta, which can be done using kinematics. The part that confused me in this problem is part e due to the wording, but I figured out that we must set sqrt(c^2+4km)=0 and then solve for the ratio of c/sqrt(km).
In Part (e), you find the damping ratio zeta in terms of the parameters c, k and m, and the set zeta = 1 (critical damping).
Are there reaction forces at the drum's pin? If there are, how do I get rid of the reaction force in the y direction in my EOM equation?
Yes, there are reactions at the drum center O. When you take the moment about O, these reactions do not appear, and therefore, you do not need to deal with the reactions.
I found it helpful to take the moment about the center of mass about the drum and to relate the velocities of A and B to their contact points to the drum and those contact points to another.
The block's acceleration does impact the problem, so drawing FBDs of both the block and the drum is very beneficial, defining a direction of X and sticking with it through the problem was easiest, and prevented errors with signs, however, either direction works as long as kinematics is treated carefully.
In this problem, it is crucial to be consistent the way you define the positive theta direction. If you stick with a positive theta in the clockwise direction as shown in the figure, then you will need to treat the counterclockwise direction as the negative direction when adding up the moments. If you do not stay consistent when your sign convention, the whole problem will be thrown off.
Is it also necessary to make an FBD for the block A? I haven't seen anyone discuss it, but if you make this free body diagram, you solve that the tension being applied by A also has the component of the block's acceleration. I got the the tension T_a = mg-m*x_ddot. As opposed to just mg if you dont make an fbd for the block. Is this a correct approach?
In part E of this problem, I found it difficult to solve the final answer if the EOM had isolated Z double dot. I recommend leaving the coefficient in front of Z double dot and not simplifying the M term, this allows many terms to cancel.
It is important to draw two separate FBDs, one for the drum and the other for the suspended block. Using these FBDs you are able to form equations using a moment equation for the drum and a sum of forces equation in the Y.
Can we use the mass moment of inertia of a uniform disk for I_o? I used it for I_o * theta'', but I'm not sure if that's the right line of thought...
Understanding the dynamics problem involves considering the directions of motion (theta and z), and how forces from springs and dashpots interact with these motions. Springs exert a force proportional to displacement, while dashpots oppose motion with a damping force. This analysis helps us model how these forces influence the system's behavior and stability.
Lecture book page 388 is very useful for remembering the topics of this problem.
For this problem, when completing the kinematics, understand that block B is 2R away from the center of the drum. Your kinematics for block A and block B will be different based on these distances from the center of the drum.
Recall that the moment of inertia for the drum is a relation of mass and radius of gyration. Also, recall the kinematic relationship between x and theta. These relationships make solving this problem much easier.
Do we have to divide by mass for the EOM in terms of z?
Do have to assume that in this scenario, that the rope is rigid and doesn't slack? And would that apply to both of the ropes in this case?
Personally when completing this problem, I fount it useful to think about the Theta and Z and make sure the radius is considered. In addition, It is also relevant since this is a spinning object to stick to which direction is positive . Lastly taking the moment about the center makes the most sense to relate the spring, dampener, and weight.
Use the fact that zeta = 1 for critical damping to help solve for Part E
I found it useful to take moment about the center 0. Additionally, the bar B should not be considered as a mass of its own and should be ignored while performing calculations.
Reminder to use the PAT based off of where you took the moment about in your system.
A good thing to mention here is that the distance travelled by the block and by the bar are different based on time. As such, the double derivative or the linear accelerations in the defined axis is different. Please do not forget this and mark them as separate variables. However, in general the block and the bar problem is quite easy to solve if three FBDs are created and summations made for each. We can then solve for the equation of motion and solve for the damping frequency which allow us to form our general solution.
Hope this helps.
Taking a moment around the center of the drum helps. Though paying attention to the signs for the forces is important as theta is positive clockwise.
I found it best to draw three FBDs, one for each object, and use kinetics to relate the two tension forces. This way you can get your EOM.
Remember that when you relate theta_dot to x_dot for block A, the radius here is only R, so it will not be the same substitution as the other system.
The kinetics for this problem is greatly useful for isolating equations for the tension forces pulling on the drum by points A and B. I took a moment about point O for the drum and used the rotational inertia about that point with the radius of gyration. I also assumed a positive direction of motion in my FBDs for points A and B as up to remain consistent in my analysis. The kinematics section will allow you to derive equations for x, xdot, and x_double_dot in terms of theta by analyzing the rotation of the drum (x being equal to theta*outer radius of drum). Combining these equations (5-6 total in my case) was a lengthy process, but the referenced derivations should allow all unknowns to be solvable.
It is important for this problem to establish early your x direction and the kinematic sign relations between x and theta in order to develop an effective EOM.
Think about how to relate linear movement to angular movement
It is important to distinguish the kinematics of Block A and Connector B, as converting them between the parameters of x and theta will result in different answers. They are different distances from the center away, resulting in different relative speeds.