| Problem statement Solution video
|
DISCUSSION THREAD
We encourage you to interact with your colleagues here in conversations about this homework problem.
Discussion and hints:
The solution for the velocity and acceleration of end B is a straight-forward application of the rigid body velocity and acceleration equations for member AB:
vB = vA + ω x rB/A
aB = aA + α x rB/A - ω2*rB/A
where vB = vB* j, aB = aB*j and aA = aA*(cos(θ)*i + sin(θ)*j). Each of the two vector equations above represents two scalar equations, providing us with the necessary equations to solve for vB, ω, aB and α. All of the observations made above can be predicted by the above kinematics equations. Instant centers (later on in the course) can prove useful in providing explanations.
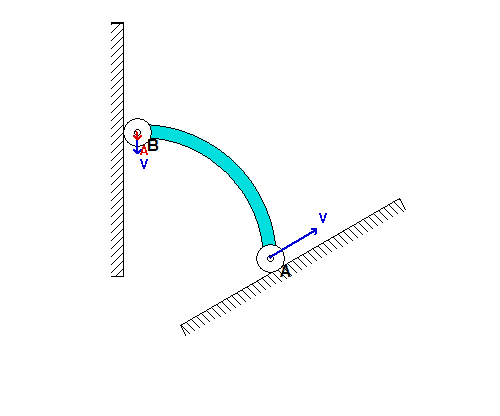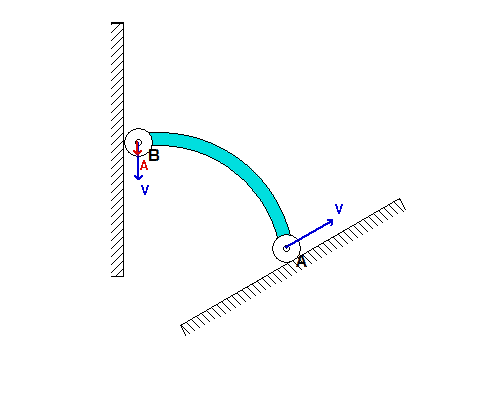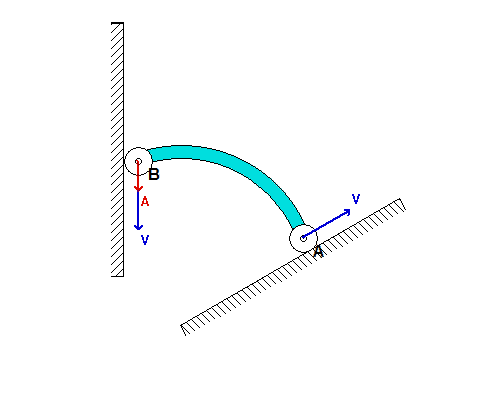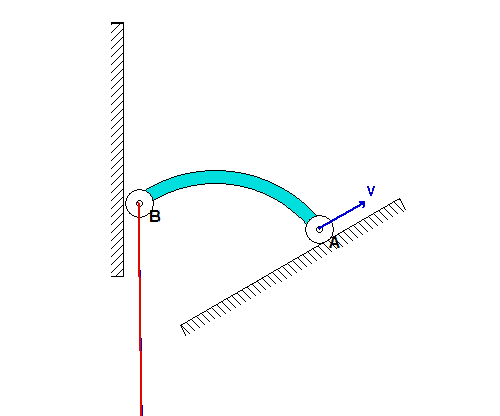
For the inclination angle used in the above simulation, we see that point B moves DOWNWARD along the vertical wall as A moves up along the incline. As B moves onto the same horizontal plane as A, the acceleration of B becomes very large (although A continues to move with a constant speed). Can you provide a physical explanation for this?

If we now consider a steeper inclination angle for A, as used above, we see that end B initially moves UPWARD along the wall; however, at some point B reverses its direction and begins to move DOWNWARD along the wall. Can you provide a physical explanation for this? Note also that the acceleration of B becomes very large as B moves onto the same horizontal plane as A, as it was for the initial value of inclination angle.
What is the value of the incline angle theta that defines the boundary between the types of initial motions for bar AB shown in the above two simulations? For the numerical value of the angle theta provided in the problem statement, which of the two simulations above agree with your results?
This problem follows a similar thought process to problem 2.A.7 in the lecture book.
Remember to look for instances where the i_hat or j_hat direction for V_b or A_b is zero. If this is the case, then the problem becomes much easier to solve for your unknown variables by treating i_hat and j_hat as its own equation.
For the vector r_b/a, are we to use the length of a quarter semi-circle in terms of R such as 1/4(2*pi*R)?
r_B/A = the vector from A to B = -r*i^hat + r* j^hat
Must we include units in our answer? None were provided in the problem statement, so I am wondering if they are necessary in our answer.
Your answer will be in symbolic form; that is, left in terms of the variables of the problem. When/if numerical values are provided for the variables, these numerical values will include units. That is, you do not need to include units on a symbolic form of the answer.
For part A, What can we do to find ω in this problem? I was thinking to assume its positive and solving for it after splitting the V_B into i and j components. Then I could use that value to find V_B in the other component. Is this a valid method to solve?
Yes, the method that you describe is the recommended one.
As a further discussion point from the hints, an interesting fact about this problem is that the turning point from positive V_B to negative V_B is when point A reaches a point where vector AB is perpendicular to the ramp. Before that critical point, V_B is positive and after that critical point, V_B is negative. This can be proven geometrically (for the sake of not making this comment too long, I'll leave that as an exercise to the reader). Therefore, in this problem, theta = 45 degrees is the critical point (as it would be perpendicular to AB) and since theta is larger than that, V_B will be positive and become negative once vector AB is perpendicular to the ramp (this can be seen in the simulation).
Yep, I agree with this! This is also why our problem, which has an angle of 53.13 degrees, agrees with the second simulation above.
The i_hat direction of the velocity rigid body equation can be used to solve for omega as the left side will be 0 and the right side will have omega as the only unknown. This can then be used to solve for v_b in the j_hat direction.
In this example, theta is greater than 45 degrees, thus this problem acts like the second simulation above. Because of this, V_b can be either positive or negative in the vertical direction depending on its position
It is important to note here that to find omega, vb must be split into i and j components. Also make sure to label aA as 0, as vA is constant. This will keep aB in terms of R and vA only.
The methodology for this homework should be nearly identical with that from HW2A. This is because when we compute our cross product, we will end up with a vector, so while it seems like 1 equation with 2 unknowns, that is not the case.
Because B only travels vertically, we know that both the velocity and acceleration of B in the x direction is 0.
The cosine of 53.13 degrees is 3/5 and the sine is 4/5 meaning that the triangle the incline makes with the x-y axes is a 3-4-5 right triangle. This may aid in simplifying calculations or in the intuition that the incline is more vertical than horizontal so the motion of B will look more like the second animation.
Since it's been established that V b follows the second simulation, I am still confused whether we should take it as positive or negative (I know that the sign changes with position).
Are we allowed to leave our answers in terms of θ or just R and v_A?
Theta is given as 53.13 degrees in the problem; the cosine of 53.13 deg is 0.6 and its sine is 0.8, which would leave the answer purely in terms of R and v_A.
When I did this problem, I ended up with the wrong answers because I messed up the signs for my cross products. Be extra careful on some of the cross products involving a lot of negative signs like for the j_hat component.
Because the angle was above 45 degrees, we can infer that B moves upward before down, as seen in the drawing above
One helpful thing to keep in mind for problems like these is, even if intuition suggests otherwise, to just leave Vb and Ab (velocity and acceleration at B) positive while solving the problem since we don't know the directions yet. When solving the problem, if you get a negative answer, it's in the negative direction, and a positive answer is the positive direction. I assumed both to be negative, so I had to flip my signs at the end. Assuming positive can just help for the organization of the problem so you don't accidentally flip a sign.
Similar to the last homework, the crucial element here is separating the the velocity and accelerating vectors into components that you know the values of so you can find the angular velocity and acceleration.