| Problem statement Solution video |
DISCUSSION THREAD
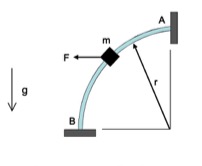
Any questions?? Please ask/answer questions regarding this homework problem through the “Leave a Comment” link above.
| Problem statement Solution video |
DISCUSSION THREAD

Any questions?? Please ask/answer questions regarding this homework problem through the “Leave a Comment” link above.
| Problem statement Solution video |
DISCUSSION THREAD
NOTE: This problem is asking for the distance that the rocket travels between when the speed is v1 and when the speed is zero (“at rest”).
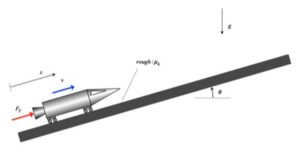
Any questions?? Please ask/answer questions regarding this homework problem through the “Leave a Comment” link above.
| Problem statement Solution video |
DISCUSSION THREAD
DISCUSSION
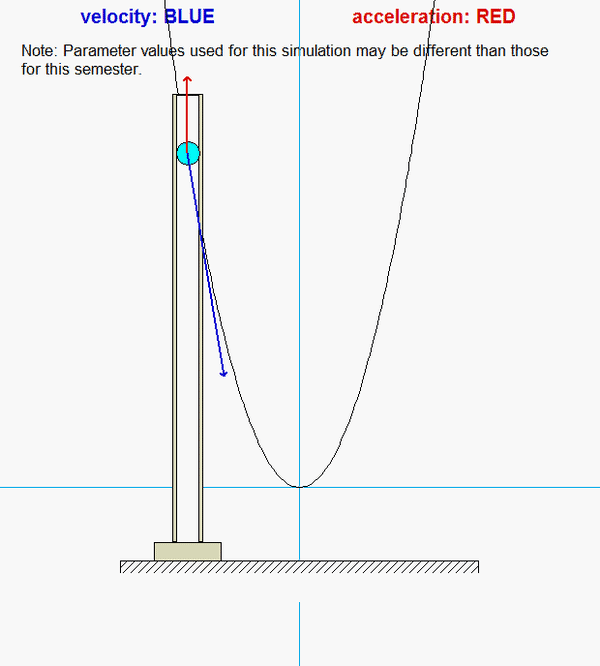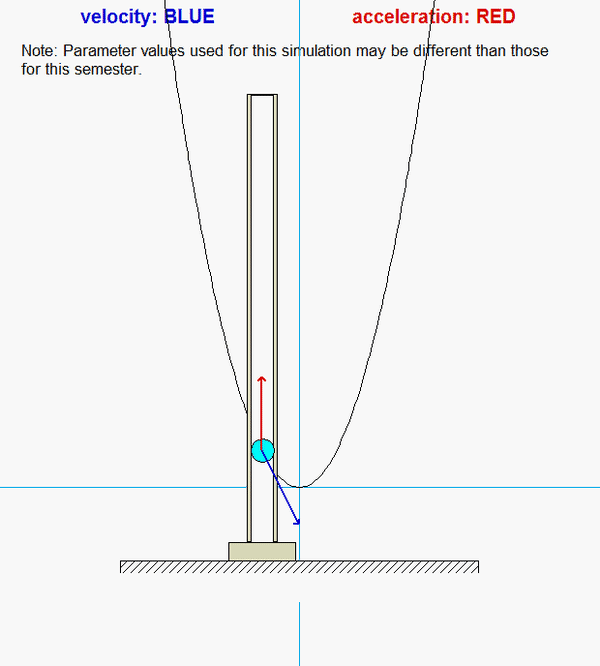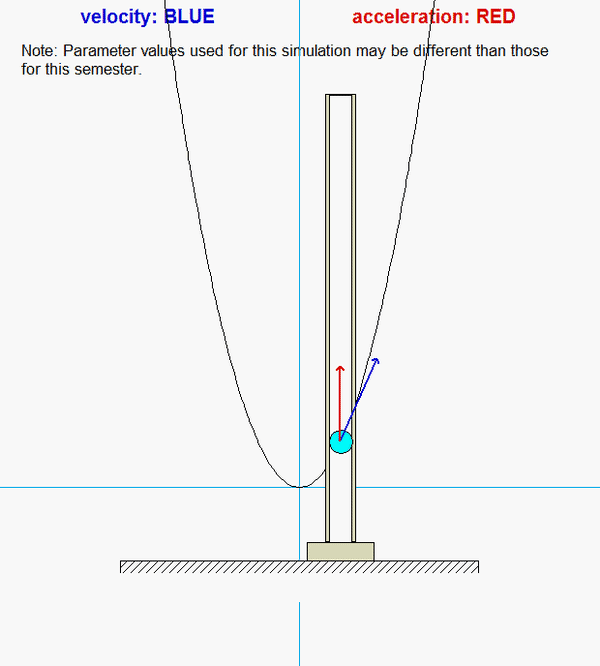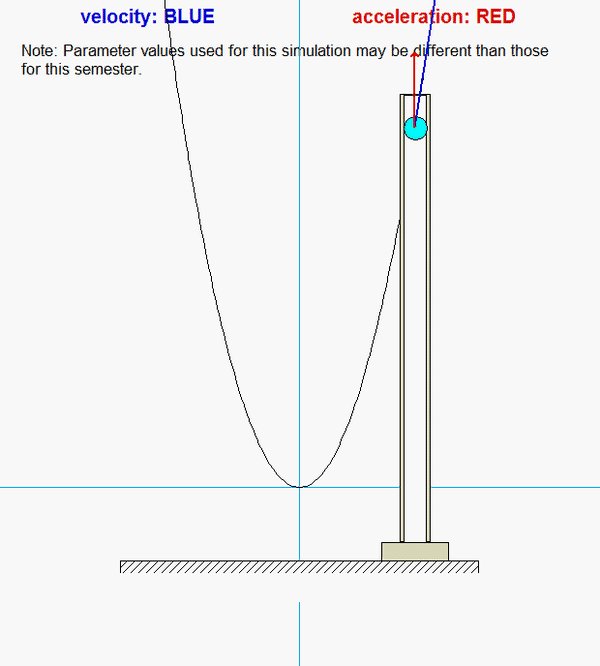
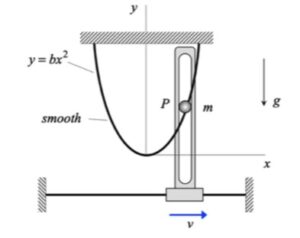
Particle P moves in a way that it is constrained to move along the parabolic-shaped guide, as well as within the vertical slot. Your task here is to determine the reaction forces acting on P by the guide and the slot that are needed to enforce these motion constraints.
As you watch the animation above for the motion of P, why is the acceleration of P always pointing in the y-direction?
Hints:
You should follow the four-step solution plan described in the lecture book, and as discussed in lecture:
Step 1: Free body diagram (FBD) – Draw an FBD of P alone.
Step 2: Kinetics – Write down the Cartesian components of Newton’s 2nd law for P.
Step 3: Kinetics – You need kinematics here to related the known x-components of velocity and acceleration of P to its y-components.
Step 4: Solve – You will have two equations and two unknowns. Solve these for the two reaction forces.
Ask and answer questions below. You will learn from both asking and answering.
| Problem statement Solution video |
DISCUSSION THREAD
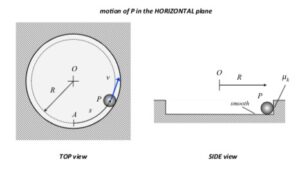
Any questions??
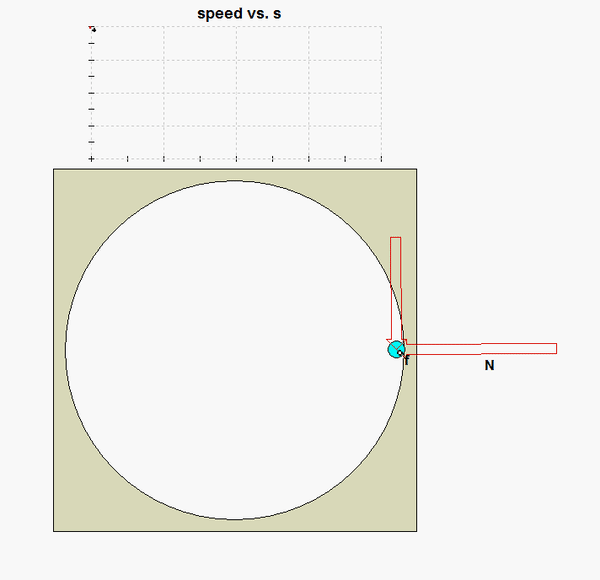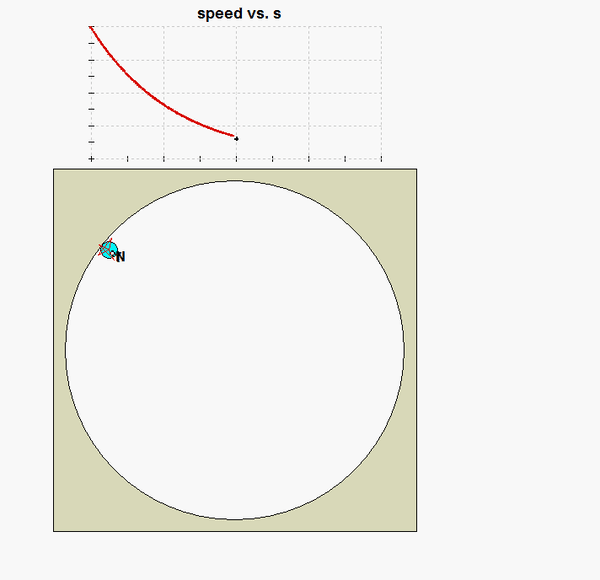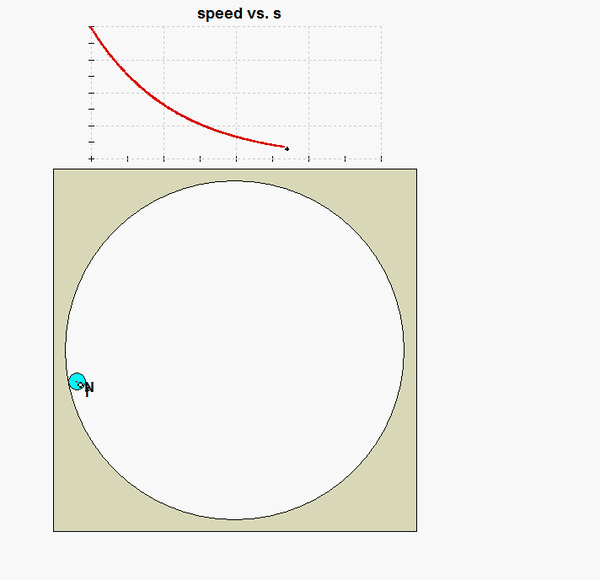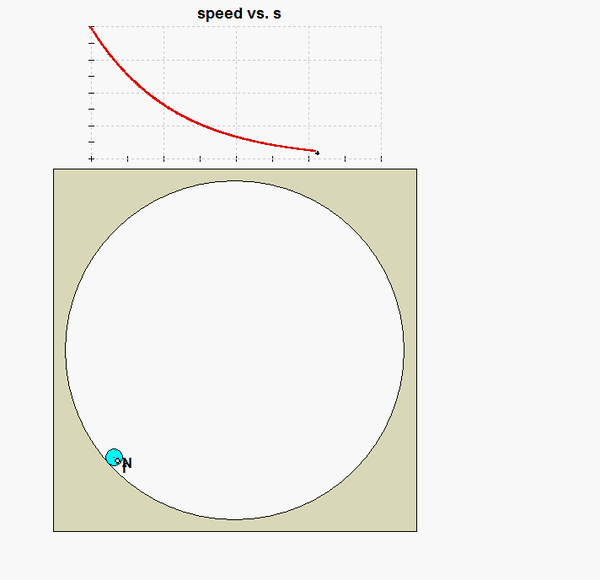
As P moves around on the circular track, two things occur:
From this, we see that the friction force goes to zero as the speed goes to zero. What does this imply about P coming to rest? Can you see this in the animation of the motion below?
HINTS:
You will need to use the chain rule of differentiation to set up this problem: dv/dt = (dv/ds)(ds/dt) = v (dv/ds).
| Problem statement Solution video |
DISCUSSION THREAD
Any questions?? Please ask/answer questions regarding this homework problem through the “Leave a Comment” link above.
Discussion
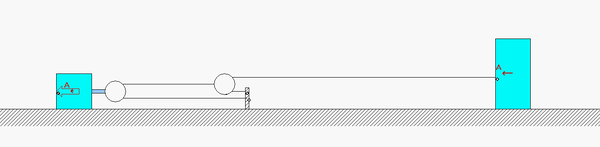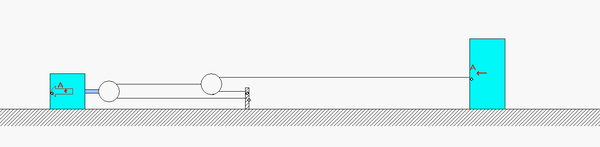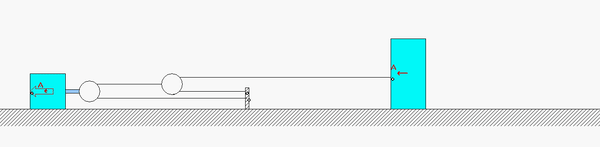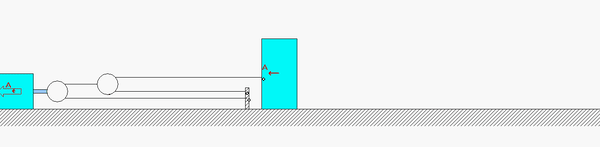
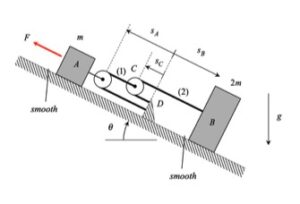
FOUR-STEP PLAN
Step 1: FBD – Draw individual free body diagrams of A and B, along with an FBD of pulley C.
Step 2: Newton – From each FBD, write down the Newton’s equation for components along the incline. Recall that the pulley has negligible mass.
Step 3: Kinematics – You will need to use the cable-pulley system kinematics that we worked with earlier in the semester. Please review the material from Section 1.D of the lecture book to relate the accelerations of blocks A and B.
Step 4: Solve – Combine your equations from Steps 2 and 3 to solve for the accelerations of blocks A and B.
| Problem statement Solution video |
DISCUSSION THREAD

Any questions?? Please ask/answer questions regarding this homework problem through the “Leave a Comment” link above.
In the animation of the simulation shown below, the RED vectors shown are the forces of reaction acting on particles A and B (such as the force on each particle by member AB, and the normal forces of reaction by the floor and wall).
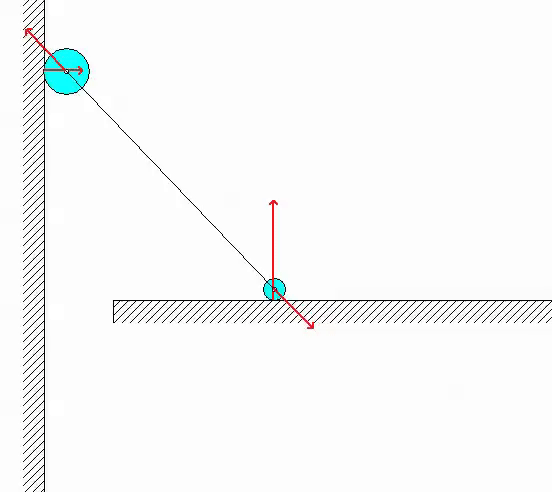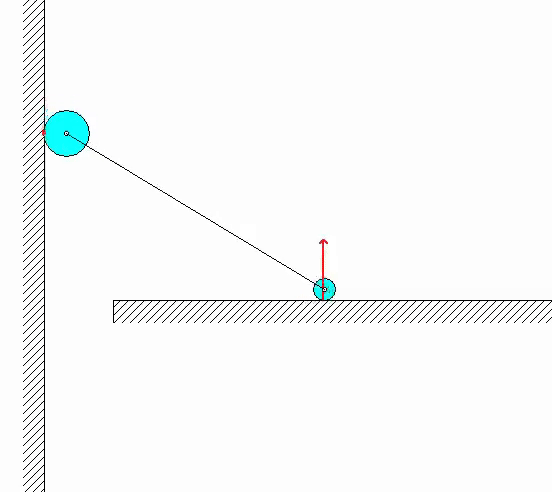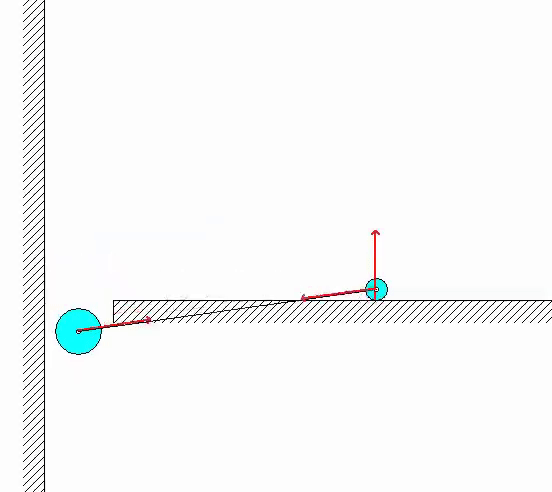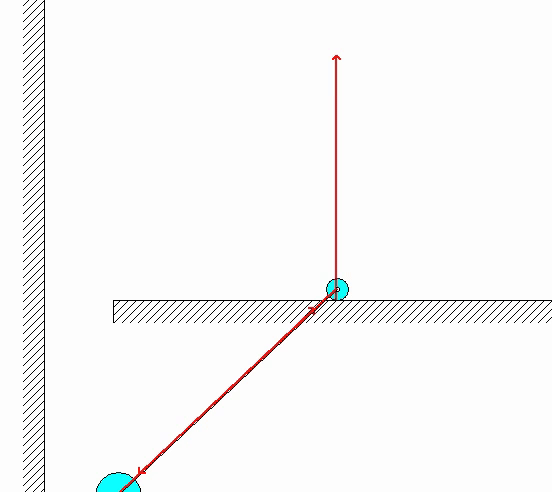
| Problem statement Solution video |
DISCUSSION THREAD
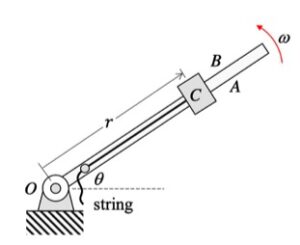
Since the motion of P is being described here in terms of polar variables of r and θ, it is recommended that you use a polar description for your forces and acceleration.
Use the Four-Step solution plan outlined in the lecture book:
Step 1 – FBD: Draw a free body diagram of C. NOTE: The arm rotates about a vertical axis, meaning that the arm moves in a horizontal plane; that is, the gravitational force acts perpendicular to the plane of the paper.
Step 2 – Kinetics (Newton): Resolve the forces in your FBD into their polar components. Sum forces in the r-direction and set equal m*ar. Sum forces in the θ-direction and set equal to m*aθ
Step 3 – Kinematics: Use the polar kinematics descriptions of ar = r_ddot – r*θ_dot^2 and aθ = r*θ_ddot + 2*r_dot*θ_dot.
Step 4 – Solve. When solving for the normal force, N, acting on C take note of the sign on your answer. What does this sign mean in terms of answering Part (c)?
Any questions?? Please ask/answer questions regarding this homework problem through the “Leave a Comment” link above.
| Problem statement Solution video |
DISCUSSION THREAD
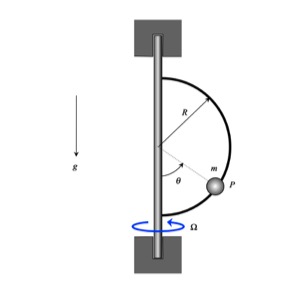
Please note that since P is not sliding on the rotating guide, P is traveling along a horizontal circular path having a radius with the radius r being the perpendicular distance from P to the vertical shaft. It is recommended that you use a set of polar coordinates: er pointing outward from the vertical shaft to O; eφ tangent to the above-described path of P; and, k pointing upward.
Use the Four-Step solution plan outlined in the lecture book:
Step 1 – FBD: Draw a free body diagram of P. With the guide being smooth, there will be only two forces acting on P: the weight and the normal force N from the rotating guide.
Step 2 – Kinetics (Newton): Resolve the forces in your FBD into their polar components. Sum forces in the r-direction and set equal m*ar. Sum forces in the k-direction and set equal to 0 (since P has no vertical motion for all time).
Step 3 – Kinematics: Use the polar kinematics descriptions of the acceleration of P. Note that r is constant for all time and Ω is constant.
Step 4 – Solve. With the above equations you will have sufficient number of equations to solve for the unknowns in the problem, which includes N and θ.
Any questions?? Please ask/answer questions regarding this homework problem through the “Leave a Comment” link above.
| Problem statement Solution video |
DISCUSSION THREAD
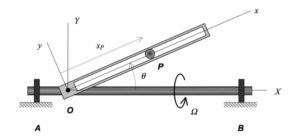
Any questions??
Discussion and hints:
Your first decision on this problem is to choose your observer. Since an observer on the tube will have the simplest view of the motion of the particle P, attaching the observer to the tube is recommended. Also, attach you xyz-axes to the tube.
Next write down the angular velocity and angular acceleration of the tube. Based on what we have been doing up to this point in Chapter 3, hopefully it is clear that the tube (and observer) has two components of angular velocity: Ω about the fixed X-axis and θ_dot about the moving z-axis. Take a time derivative of the angular velocity vector to find the angular acceleration of the tube (observer).
Following that, determine the motion of the particle P as seen by the observer on the tube.
Use these results with the moving reference frame kinematics equation to determine the velocity and acceleration of the particle P.
| Problem statement Solution video |
DISCUSSION THREAD
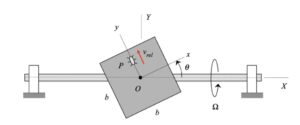
Any questions??
Discussion and hints:
Your first decision on this problem is to choose your observer. Since an observer on the plate will have the simplest view of the motion of the insect, attaching the observer to the plate is recommended. Also, attach your xyz-axes to the plate.
Next write down the angular velocity and angular acceleration of the plate. Based on what we have been doing up to this point in Chapter 3, hopefully it is clear that the plate (and observer) has two components of angular velocity: Ω about the fixed X-axis and θ_dot about the moving z-axis. Take a time derivative of the angular velocity vector to find the angular acceleration of the plate (observer).
Following that, determine the motion of the insect as seen by the observer on the plate.
Use these results with the moving reference frame kinematics equation to determine the velocity and acceleration of the insect.