| Problem statement Solution video |
DISCUSSION THREAD
Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.
Discussion and hints

| Problem statement Solution video |
DISCUSSION THREAD

Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.
Discussion and hints

Comments are closed.
This problem is similar to the ones shown in class, however, I would pay attention to the damping ratio as this can be a good indicator on what equation to use for the following step.
Are the units of c something we should worry about? Realizing this value makes the damping ratio is quite small, so the frequencies came out nearly the same for me.
I'm wondering about that too. Can we use four significant figures to show the change instead of the usual three?
Hayden,
Yes, you should always check the units on terms that you obtain through analysis. If the units are not correct, that is a flag that you have make an error. In SI, the units on c will be kg/s or Ns/m.
The damping ratio is actually not that small. See the animations on the following course webpage: https://www.purdue.edu/freeform/me274/course-material/animations/influence-of-damping-on-free-vibrations/
For light damping, omega_n and omega_d are effectively the same.
If my value is close to the zeta = 0.05 is it too small?
No, that isn't too small as I got a value close to that as well.
I believe this is incorrect. When solving for zeta, make sure you set c equal to 2*zeta*omega_n. Keep in mind that the expression for omega_n contains 4k, not k.
Be careful. The coefficient of 2*zeta*omega_n = c/m (NOT equal to c).
I got a value close to that as well.
No, you should not worry about the units for c. I also got a very similar number for the damped frequency as the normal frequency, but it is slightly lower if you use 3 or 4 significant figures.
What are the units for zeta?
I believe it is unitless, being a 'ratio'.
The damping ratio is dimensionless.
Don't forget to use the coefficients of your EOM when calculating the frequencies and damping ratio, not the given values of m, c, and k.
To add on/clarify, the coefficients also include the given values of m, c, and k.
You can find the EOM in x from the sum of forces of "x". From there, you should then find ways to relate the terms in the EOM to the natural frequency and zeta. Since this problem involves light damping, the damped natural frequency should be close in value to the natural frequency. If not, you might've made a mistake somewhere. Question: In the problem statement, it says x = 0m when the springs are unstretched. Is this x naught? This is crucial when solving for the variables in part d.
The statement that x = 0 corresponds to the fact that when the springs are unstretched x = 0 (that is, F_sp = k*x).
By coincidence, in this problem the system is released with the spring unstretched, that is, x(0) = 0. In general, that will not be true.
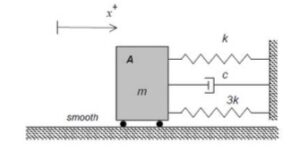
When solving this question, it's important to keep in mind that the block is not spinning, and therefore the moment equation is useless. Instead, focus on the sum of forces.
This question is very similar to Example 6.B.9, and pg 392 & 394 are a great aid in answering and understanding this question. Where it's important to keep the sign convention in mind for the EOM.
Should we assume that the dashpot has a force acting in the same direction as the spring forces?
This is the standard assumption if placed in the same location, dashpots dampen motion, so the resulting force, c * x(dot), or c * velocity, acts in the negative x of this given system.
Yes, since you assume motion to the right, the springs and the dashpot are being compressed meaning all of the forces would act to the left.
Make sure to pay attention to if the system is over, under, or critically damped, because this will determine the equation for the response of the system.
The dashpot damping and spring force should be pointing in the the same direction to allow you to have all positive components in your EOM.
Remember to use the correct equation for the response of the system, based on the damping ratio.
For this problem I found it helpful to start of with a force equation in the x direction. This gave me the EOM and I converted it to standard form (coefficient of one on x''). The standard form can be used to find variables in part c. I also referenced the information in chapter 6 of the textbook to help solve.
The equation for damped natural frequency w_d for an underdamped case can be found on page 392 of the textbook.
Remember to check the zeta value to find if it is an under damped , over damped or critically damped scenario and then you can use the corresponding equations.
I found this problem to be similar to example 6.B.9 in the book.
For part d, remember the initial condition is x=0 this in addition to x'=4 can be used to solve for all the missing values by using the x(t) equation and its derivative. This will give you the response of the system equation.
x(0) is 0, right?
At t = 0, the springs are unstretched. Since x = 0 when the springs are unstretched, then, yes, x(0) = 0.
How do you determine if the system is under, critically, or over damped, numerically?
It’s under damped when 0<ċ1 where ċ is the damping coefficient. Ċ = 2/(C*root(KM))
Steps:
• Derive the EOM (draw FBD(s), write down the Newton/Euler equations, write down the kinematics, and combine altogether to get a single second-order differential equation in terms of the single dependent variable representing the motion, let's say "x").
• Put the EOM in "standard form" by dividing through by the coefficient in front of x_ddot.
• The coefficient in front of the x term is omega_n^2. Use this to solve for omega_n.
• The coefficient in front of the x_dot term is 2*zeta*omega_n. Use this to solve for the damping ratio, zeta.
• If 0 ≤ zeta <1, then the system is underdamped.
Does this help?
this question is super similar to question 6B.8 but without the angle. hope that helps!
The summary slide on vibrations - damped free response is helpful in summarising the necessary equations to solve this problem. It is important to create a standard form of the EOM before continuing with the computations.
To determine if a system is under, critically, or over damped, numerically, first check your c constant. If it is 0, the system is undamped. If it's not 0, solve for zeta. When zeta is between 0 and 1, the sys is underdamped. When zeta is 1, the sys is critically damped. When zeta is greater than 1, the sys is overdamped.
When completing this problem it was noticed that there are a few good examples in the lecture book that outline the necessary equations for this problem. I would also recomend being careful with the rules of dampened and over dampened to make sure you pick the correct one.
Here are some more useful tips:
- remember to draw a conclusion from you zeta value in order to get the proper equations for your next step
- the problem mentions both equilibrium and when the springs are untrenched
- book problems 6B6-6B9 are super useful
For this problem, I approached it like the problems in lecture. Draw a FBD, derive the equation of motion, convert it to standard form, and find the natural frequency, dampening coefficient, and damped frequency from the coefficients in the standard form equation. Then plug it in to the general solution and use the initial position/velocity values to find x(t)
Well said
Thanks
For this problem, your zeta is likely going to be very small. This means when you go solve for omega_d, it will be relatively close in size to omega_n.
I found zeta to determine which case the problem fit in to then use the right characteristic equation. Then I treated it like an initial value problem to find the coefficients.
For this problem make sure to check the damping coefficient as zeta value must be between 0 < zeta < 1 in order to proceed with the problem.
omega_d = omega_n (sqrt(1- zeta^2)), in the end omega_d and omega_n should be about the same since zeta << 1.
For positive components in your EOM, ensure that the damping provided by the dashpot and the force exerted by the spring are aligned in the same direction.
Remember that the damped natural frequency (w_d) is not the same as the natural frequency (w_n) even if they are very similar with light damping. Both are used in the final equation
When Solving this problem I found it helpful to relate my x(t) equation to velocity first, solve for one of the coefficients, then relate this to x(t) and find my other coefficient
In solving this problem, note that since the block isn't spinning, the moment equation won't apply. Focus on the sum of forces. This resembles examples discussed in class, but pay special attention to the damping ratio—it'll guide you in choosing the correct equation for the next steps.
It is important to remember to use the chain rule when you take the derivative for step D. A lot of the values will then be able to be crossed out leaving a simple answer.
Page 390 has equations that helped for parts c and d. When solving for the x(t) equation and its derivative, previous calculus knowledge comes in handy in order to find the values of the C and S coefficients.
The trick that helped me the most when labeling forces for types of problems like these is to think of the block's direction of forward motion (positive x), then determining the reaction of that movement take place, in this specific case it means all forces in the x are opposite to the direction of motion. Make sure to make the equation of motion standard form first in step C, easy mistake if moving quickly on an exam or through a homework problem.
It is important to remember the chain rule when taking the derivative in part D. This makes calculations go through a lot smoother. 🙂
Is it just the steps shown in the concluding remarks slide?
This problem is pretty much straightforward. I set up my force x and equations, got the EOM, and used the frequency equations with the mass and spring stiffnesses from the EOM to find the system response
The equations listed on the summary of "free, damped motion" listed under the daily schedule tab on the ME 274 website are very helpful for this problem. However, be careful to not just skip to the simplified forms since they do not account for the fact that there is multiple times the k value.
Thank you for pointing this out. I found that a good way to get around this is to calculate the coefficients of the EOM (which are different from the given m, c, and k values), and then use those coefficients to calculate the quantities needed to directly plug into the simplified equations.
I found it easiest to solve this question by first finding the sum of forces in the x-direction, which gives us the EOM. From this, you can find the values for the damping ratio and the frequencies. To determine the response of the system, don’t forget to use x(0)=0 and xdot(0) =vo.
Should our EOM equation be in standard form?
I don't think it should matter as the problem doesn't specify, it just asks for a single EOM with the given variables. Either way the equations are equivalent.
The current material in MA 262 (Lin Alg & Diff Eq) is very applicable to this problem. Knowledge of differential equations and damping problems can be very useful in this homework.
After finding your EOM, you need to set x_ddot and x_dot=0 and solve for x/x_st to find the value of the static deformation. This can be used to define the EOM in terms of z and helps find the natural frequency and zeta.
Would there ever be a situation similar to this in which the force from the dashpot would not be in the same direction as the springs assuming they are all on the same side of an object?
Are we to assume the forces from the spring and dashpot to be acting negatively on the block because it moves to the right?
It is not really an assumption. Put the body in a position that corresponds to a positive displacement of the body (pay attention to the sign convention(s) that are defined for the body). When in that positively-displace position, reason out the direction of the spring force.
• If this position corresponds to the spring being stretched, in which direction is this spring force on the body?
• Or, if this position corresponds to the spring being compressed, in which direction is this spring force on the body?
These are the questions that need to be answered in order to determine the directions of the spring forces.
Assuming block A is displaced positively to the right, then the springs are under compressions. This results in a spring force acting on the block in the negative direction (left).
The summary for this lesson was beneficial in solving for C and S as they give examples and direct equations.
For this question, I found it helpful to find the direction of force by the springs first before finding the dashpots.
When determining which direction to draw the arrows for the forces from the springs, I find it helpful to imagine which direction the system would go if it was pulled in the direction of positive x then released.
One important thing to remember is that the coefficients of the x_double_dot, x_dot, and x must all have the same sign. One easy thing to check if you are doing the homework problem properly is once the EOM is solved and put into standard form these terms should all have the same sign.
It is important to remember that the damper will be working in the opposite direction of your springs in your FBD, this is apparent when you observe the animations given.
Actually, the opposite is true. The signs of all 3 components must be in the same direction, or you will run into issues further down the line.
Keep in mind the conclusion from the challenge question on page 394. It goes over how the signs of the 3 coefficients should be the same, otherwise, your Wn would be an imaginary number. In this problem, this would mean that mx_doubledot should be opposite of the forces of the springs and dampeners.
It might be helpful to look at the question 6.B.9 from the course lecture it is pretty similar, just keep in mind that variables for the response equation need to be setup slightly differently.
I found it useful for this problem to avoid issues with parts C and D with the use of the summary slides in the daily discussion and utilizing a system of equations to produce a solution. Also, it helps to remember the value of x when the spring is unstretched to find the x_o.
Are the rules for series and parallel combinations for springs the same for combining series and parallel dashpots?
Page 393 shows the basic setups for various shapes, and a setup like this is shown on there.
For this problem, It might be helpful to review the equations in the summary section of this week which will include the equations to find Wd, Wn, as well as the response coefficients.
When solving for x(t) in part d, you can use the assumption that x(0)=0 to solve for one of the missing variables in the equation. From there, you can use the derivative of x(t) to solve for the other missing variable.
I found this problem interesting because the force from the springs and the dashpot act in the same direction in the FBD. This seems somewhat counterintuitive to me because the springs cause the motion while the dashpot dampens the motion.
note whether the system is over-, under-, or critically damped, as it will dictate the equation governing the system's response.
Wouldn’t the period be the same with or without the dampener?
Typically, without a damper, the system would oscillate indefinitely at its natural frequency and adding a damper would dissipate energy, causing the amplitude of oscillation to decrease over time and slowing down the oscillations. This results in a longer period of oscillation compared to the undamped system. However, in the case of a tuned or extremely weak dampener, the period may not be affected but this is extremely uncommon.
Are there units for the dampening constant, or does it have no units?
One of the things I struggled with in this problem is thinking that the two wheels of the cart would impact is motion. However since it is not tipping and we mostly look at the forces in the x direction , it is actually not necessary to take them into consideration.