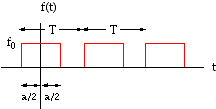
Fourier Series of Square Wave

---

In Example IV.2.1 we studied the Fourier series for a periodic square wave:

Shown below is an animation showing the influence on the addtion of terms in the Fourier series to produce this periodic square wave. Note that as more terms are added, the square shape appears; however, oscillations also appear near the discontinuities in the wave. The appearance of these oscillations is often referred to as the "Gibbs phenomena".

 

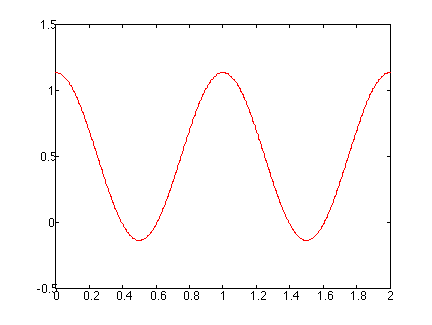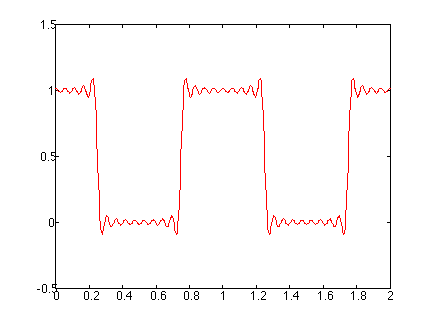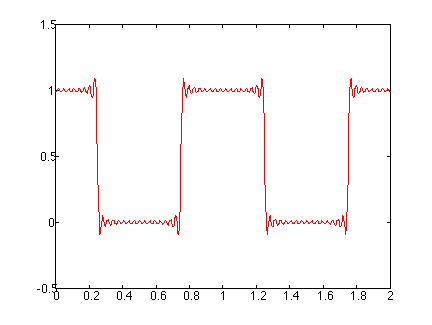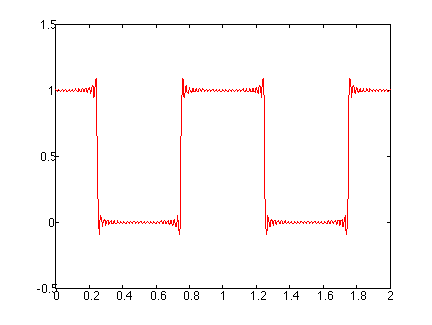
We had a hint that this might happen. Look back at Dirichlet's theorem in the lecture notes. There is says when discontinuities appear in the forcing, the resulting Fourier series will converge to the mean value of the forcing. Here we have oscillations that persist regardless of the number of terms included in Fourier series; however, you can see that the series does converge in the average sense to the actual forcing.