Flexibility Matrix: Animations

In this lecture we discovered the principle of "reciprocity" for the static deflection of linear systems.

• The MATHEMATICAL consequence: The flexibility matrix [A] is symmetric.
• The COMPUTATIONAL consequence: We need to only calculate the upper (or lower) triangular portion of the [A] matrix due to reciprocity.
• The PHYSICAL consequence: Applying a force at location "i" gives the same deflection at location "j" as one would get at "i" due to the same force applied at location "j".

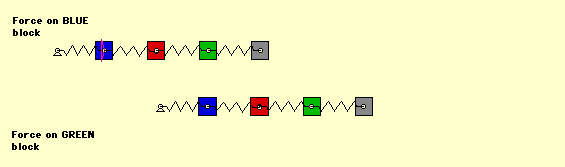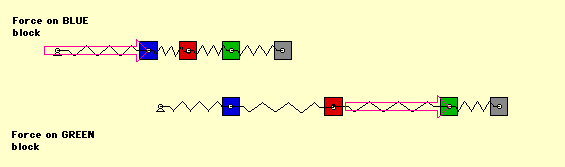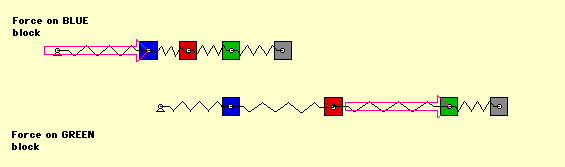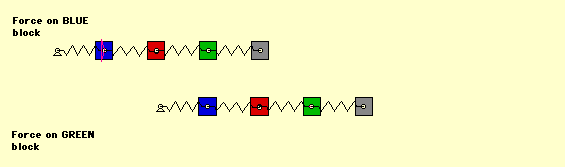
  As an example, consider a four-DOF spring-mass system. The reciprocity principle says that applying a force F on mass 1 (blue) will produce the same deflection at mass 3 (green):

  
  as the deflection of mass 1 (blue) due to the same force at mass 3 (green):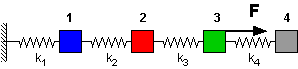
  This reciprocity of forces and deflections is valid regardless of the stiffness values of the springs. Consider an animation of this example shown below. In the top part of the frame, the force is applied to the blue mass, and in the lower part of the frame the same force is applied to the green mass. From reciprocity, the static deflection of the green mass in the top part of the frame is the same as the deflection of the blue mass in the lower part of the frame. (Note that the system in the lower portion of the frame has been shifted to the right to align the green mass on the top with the blue mass on the bottom.)