The Convolution Integral

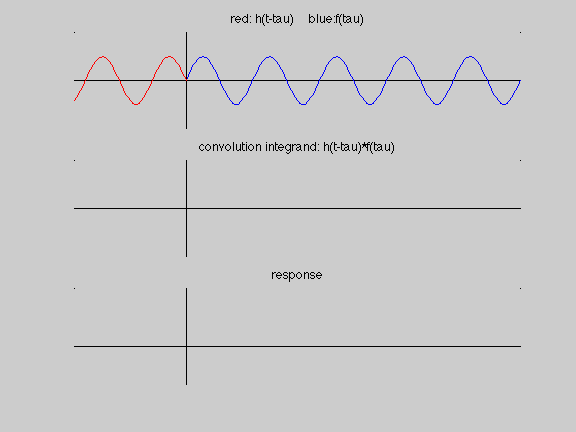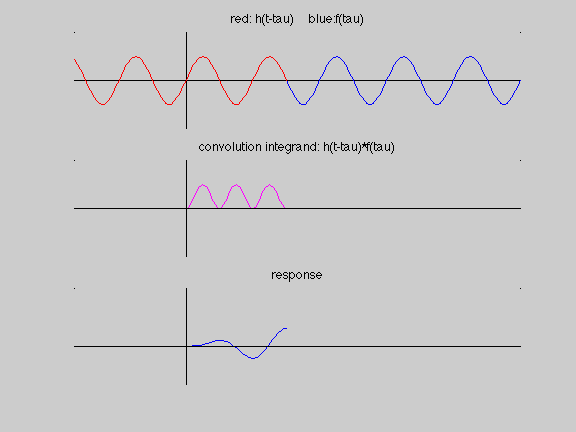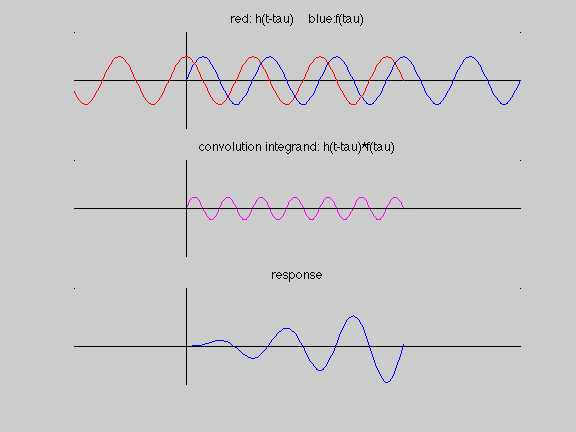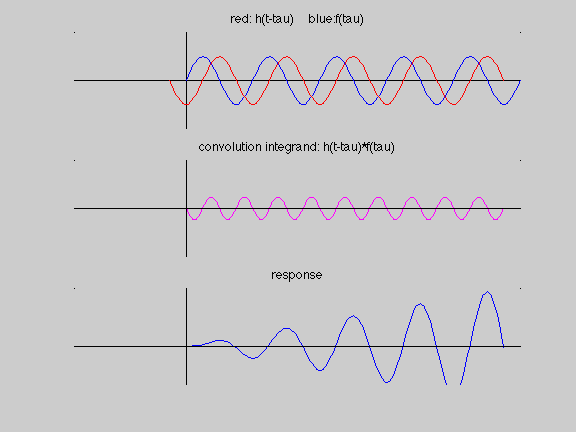
Recall  that the convolution integral process is broken down into four steps:

• folding the impulse response function: h(tau) folds to h(-tau)
• shifting the impulse response function: h(-tau) shifts to h(t-tau)
• multiplying the folded/shifted impulse response function with the excitation: h(t-tau) f(tau)
• integrating to find the area under the h(t-tau) f(tau) curve

In the following animation, we see this four-step process to aid us in interpreting the resonance response of a single-DOF oscillator to harmonic excitation. From this, we see that the response amplitude is linearly increased as we move along in time. This is due to the lining-up of the shifted/folded impulse response function with the excitation.

(ANIMATION AUTOMATICALLY REPLAYS)

 

---