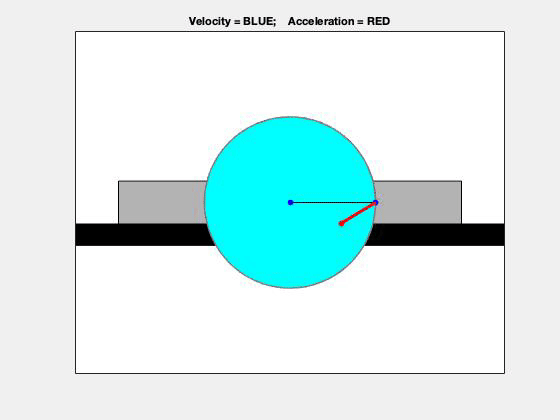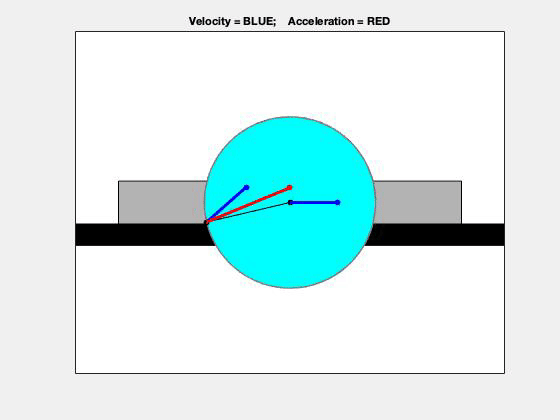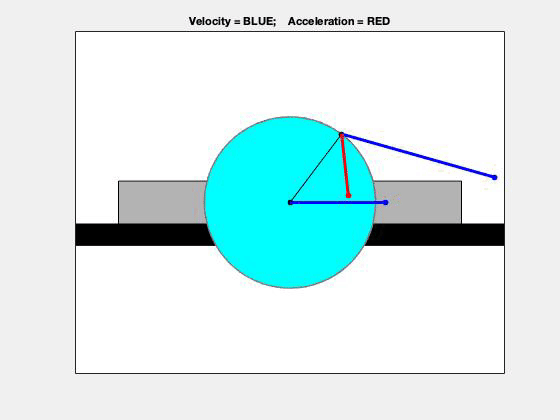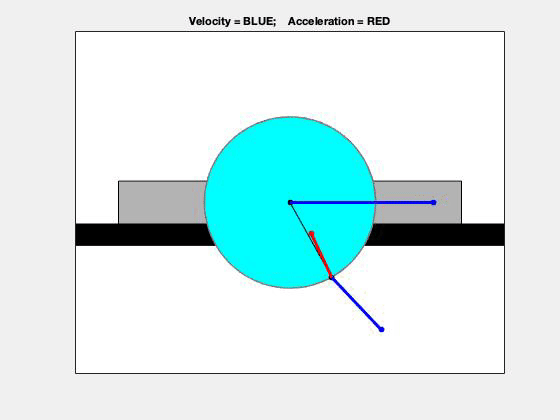
| Problem statement Solution video |
DISCUSSION THREAD
Any questions??
Discussion and hints:
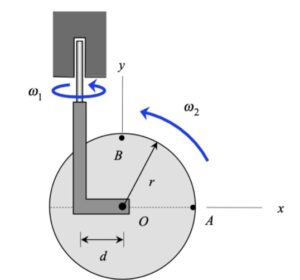
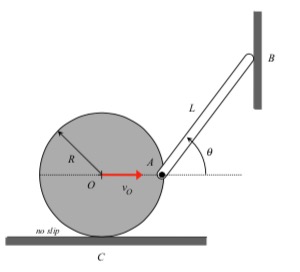
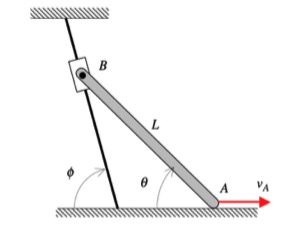
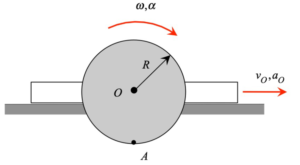
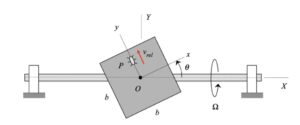
Your first decision on this problem is to choose your observer. Since an observer on the plate will have the simplest view of the motion of the insect, attaching the observer to the plate is recommended. Also, attach your xyz-axes to the plate.
Next write down the angular velocity and angular acceleration of the plate. Based on what we have been doing up to this point in Chapter 3, hopefully it is clear that the plate (and observer) has two components of angular velocity: Ω about the fixed X-axis and θ_dot about the moving z-axis. Take a time derivative of the angular velocity vector to find the angular acceleration of the plate (observer).
Following that, determine the motion of the insect as seen by the observer on the plate.
Use these results with the moving reference frame kinematics equation to determine the velocity and acceleration of the insect.