DISCUSSION
In this problem, the x- and y-components of the position of the bottle are prescribed functions of time. The Cartesian components of velocity and acceleration for the bottle are found directly through the time derivatives of these prescribed functions of time.

Please ask and answer questions here. Either way, you learn.

Discussion and hints:

In this problem, the xy-Cartesian components are constrained through the equation of the path of P:  x² + y² = R².  The x-component of the position is an explicit function of time. Finding the time derivatives of x is done through simple time differentiation of x = b sinωt. The derivatives of y with respect to time is found through the time differentiation of the constraint equation: x² + y² = R². Please review the examples worked out in lecture to assist you in this differentiation.

The results of this analysis are shown in the animation below. From this animation, we see that the velocity of the P (shown in BLUE) is always tangent to the path of P. The acceleration (shown in RED) is not quite so simple: it has components both tangent and perpendicular to the path; however, the component perpendicular to the path always points inward on the path. Both of these observations are consistent with what we see in the next lecture when we develop the expressions for velocity and acceleration in terms of their PATH components.

Any questions??

DISCUSSION
The path variables of radius of curvature ρ and speed v are provided in terms of the distance traveled variable s. Please recall that the time rate of change of speed v_dot that appears in the acceleration vector is (as the name implies) the derivative of v with respect to TIME. Since we know v as a function of position and not time, we need to use the chain rule of derivatives to find the rate of change of speed:  v_dot = dv/dt = (dv/ds)*(ds/dt) = v*dv/ds.

Please ask and answer questions here. Either way, you learn.

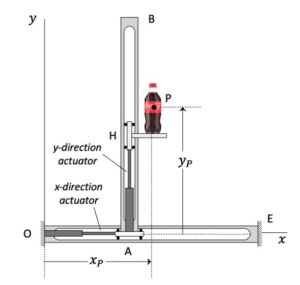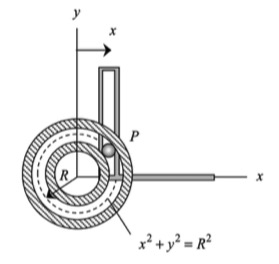
Discussion and hints:

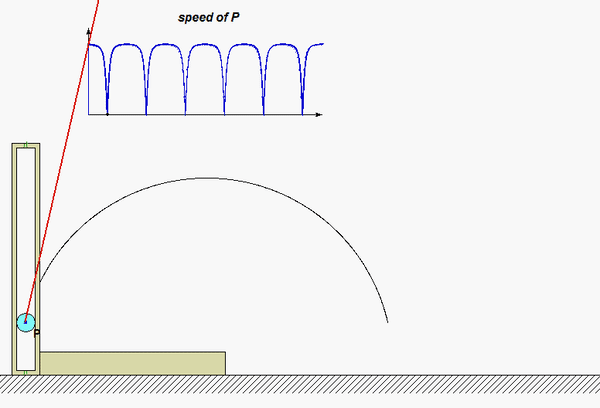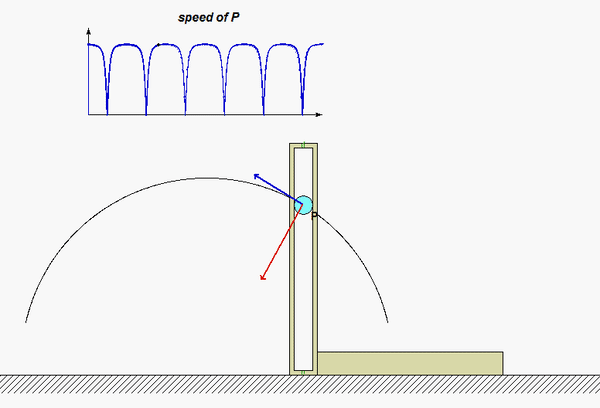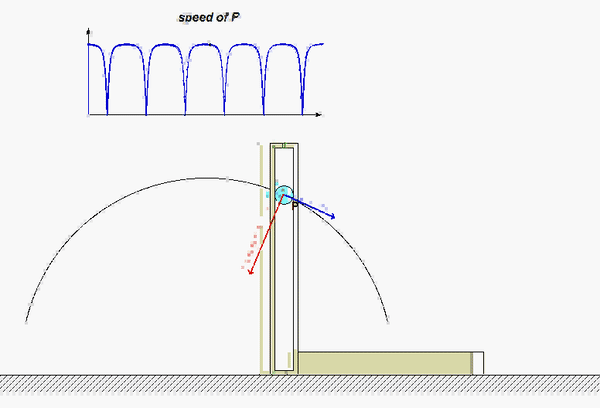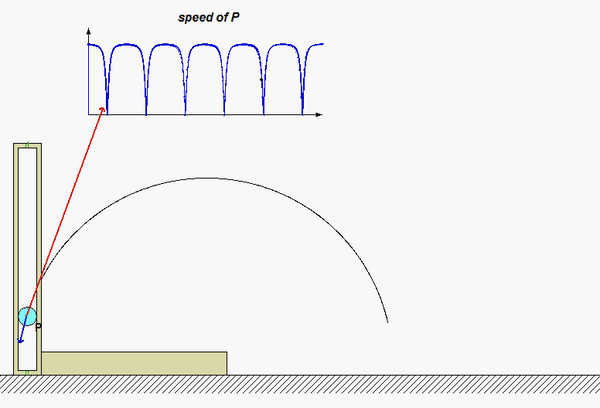
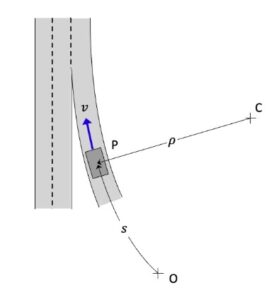
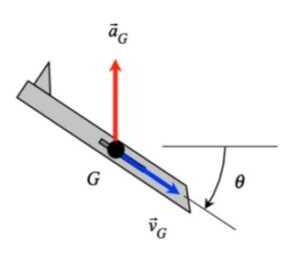
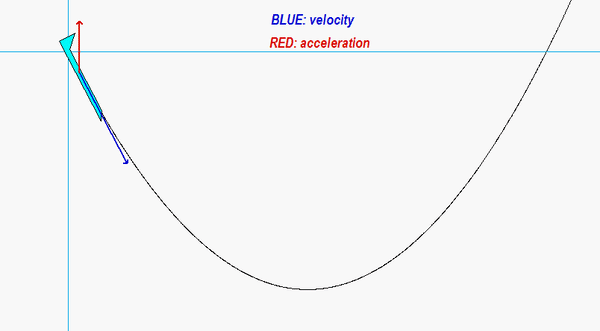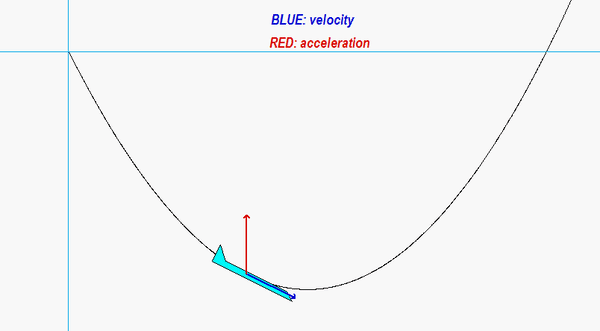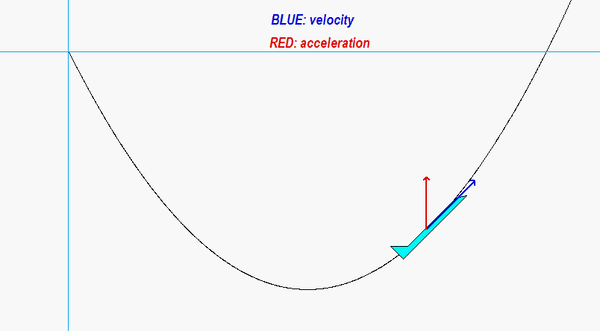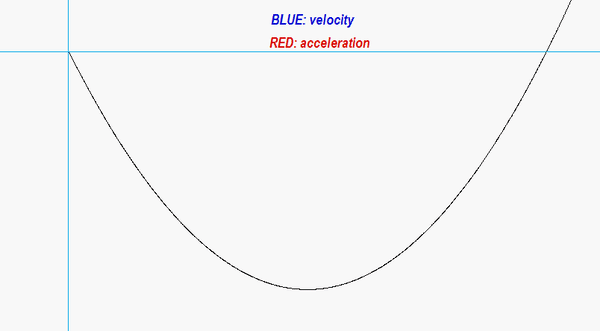
In this problem, we know both the magnitude and direction for each of the velocity and acceleration vectors for the center of mass G. We know that the unit tangent vector e_t is in the same direction as the velocity vector v_G. The unit normal vector e_n is perpendicular to e_t, and points “up and to the right” (do you know why?). Projecting the acceleration vector a_G onto the unit tangent and unit normal vectors gives us the information that we need to find the rate of change of speed and the radius of curvature of the path.

Carefully watch the animation below of the motion of the aircraft. When the acceleration vector shown in RED points “backward” from the direction of travel, the aircraft is slowing down; that is, the rate of change of speed is negative. Conversely, when the acceleration vector is “forward” of the direction of travel, the aircraft is increasing in speed with a positive rate of change of speed. If you follow this logic, you are on your way to understanding the usefulness of the results of the path description of kinematics!

Any questions??