| Problem statement Solution video (PDF providing four different versions of the solution) |
DISCUSSION THREAD
Discussion and hints:
For this problem, the “Given” information is in terms of the path kinematical description. The “Find” asks for parameters that are part of the polar kinematical description.
The key to the solution of this problem is being able to correctly draw the sets of path and polar unit vectors.
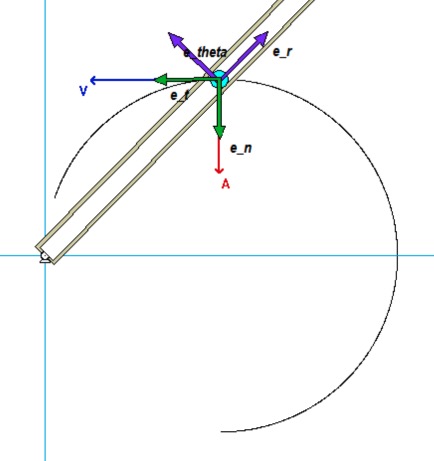
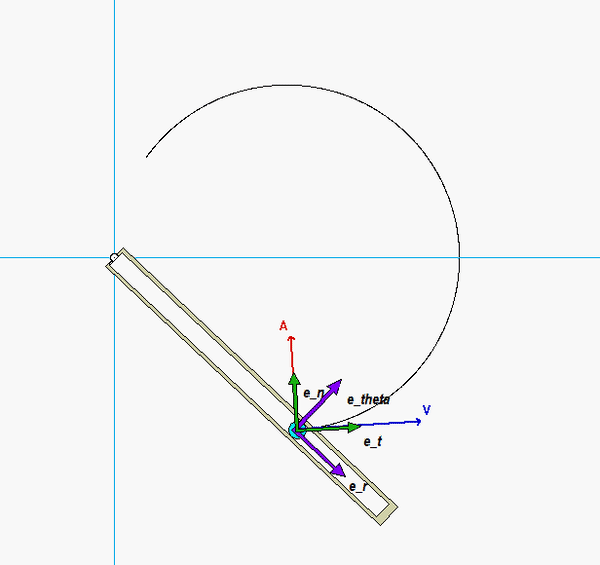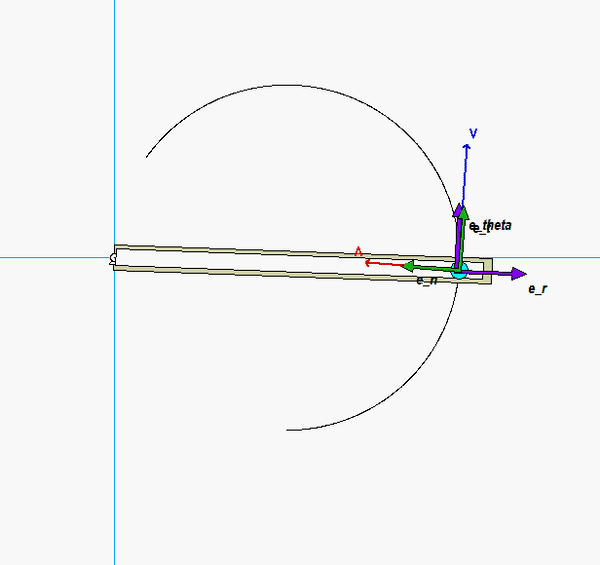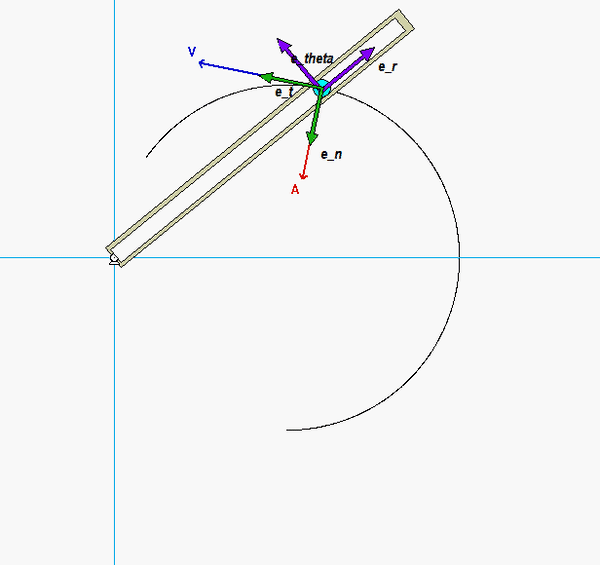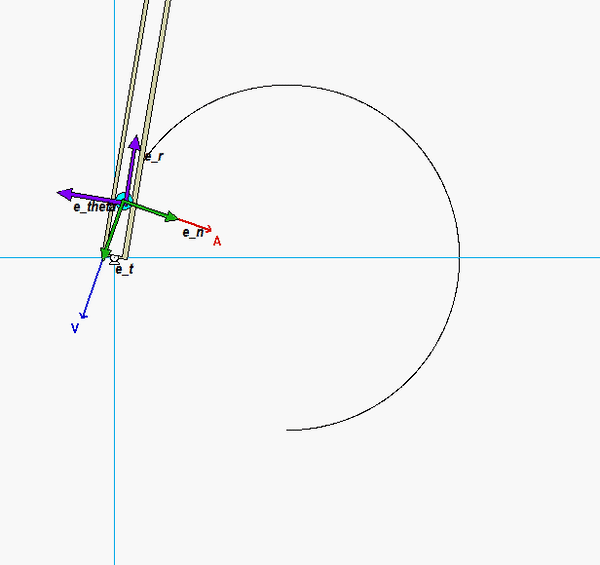
- The path unit vectors et and en are tangent and perpendicular to the circular slot (the path).
- The polar unit vectors are defined as: er points outward from O to P (along the slot in the arm), and eθ in the direction perpendicular to er (perpendicular to the slot) and in direction of increasing angle θ (counterclockwise rotation from er).
For the position of interest (θ = 45°), these vectors are as shown below.
It is recommended that you write the polar unit vectors in terms of the path unit vectors, use projections of v and a onto the polar unit vectors to produce four equations for the four unknowns. (There are a number of equivalent ways to solve this problem involving either vector projections or balancing of coefficients in the kinematics equations, as detailed in lecture and in the lecture book.)
Warning: Do not confuse the roles played by “r” and “R” in this problem.
The animation below shows the results of this analysis over a range of angles θ. There is an interesting result here. These results show that the acceleration vector is always perpendicular to the path (the circular slot). This is rarely the case. What is special about this problem that makes it true here? HINT: Think about the relationship between the angle of rotation of the arm and the angular rotation of P around the circle.
Any questions??
The only way I can think of solving this question is by creating a function for the path in polar coordinates. However, I feel like that was not the intentions of this question. Is my approach of trying to derive a path function correct?
This is a problem involving a “joint description” of the kinematics of point P: some information about the motion of P is known in terms of the path and some information is know in terms of the polar description. Therefore, we need to deal with both descriptions, as outlined in lecture on Wednesday.
As recommended in the Discussion above, you should start out by drawing in the path and polar unit vectors for the position of interest (for theta = 45° where P is directly above the center of the path C). From this figure, write down the polar unit vectors (e_r and e_theta) in terms of the path unit vectors (e_t and e_n).
Then use projections such as the following to get four equations for four unknowns:
r_dot = v•e_r
r*theta_dot = v•e_theta
r_ddot – r*theta_dot^2 = a•e_r
r*theta_ddot + 2*r_dot*theta_dot = a•e_theta
Alternately, you can use an approach of balancing coefficients of unit vectors to arrive at four equations and four unknowns, also outlined in the lecture book.
To find the distance between the observer and the point P, could I realistically use cartesian points based on knowing that point P is at pi/2 or 90 degrees on the circle and that the observer is at pi or 180 degrees. With that, could I use the known radius of 8 in, to show I have the observer at (-8,0) and point P at (0,8) and find r to be r=(x^2+y^2)^.5?
Or, just simply: r = sqrt(2)*R
Oh, ok that makes sense, thank you!
Could r be defined as a function of theta, such that r = 2R*cos(theta) to solve for r_dot and r_dot2?
You could. Sure.
The goal of this topic in the course is to get experience in working with projections to relate the kinematics in two different coordinate systems. For most of the problems we will not know the equation for the path. For those problems we will need to rely of the process discussed above and not on differentiation of the path. It is good to learn this method as it covers more types of problems.
How did you arrive to r = 2Rcos(theta) ?
You do not need to know the equation for the path of P. You only need the radial distance “r”, which from the above discussion thread is sqrt(2)*R. The four values that you are asked to find you get straight away from projections of velocity and acceleration.
I projected ehatr and ehattheta in terms of ehatn and ehatt but I am confused how to use the projection equations after that to solve for rdot, rdoubledot, and vdot. In lecture, we were given v so we could easily solve for the components but here, we are not. How should we approach the second step to this problem?
As we did in class, the projections of v and a give us four equations in terms of four unknowns. Simply solve these four equations for the four unknowns.
I got stuck here too, but realized if you use the equation r(theta_dot) = (-cos(theta))v , you have everything but v and can solve v from there! For r you use what was mentioned above of r= sqrt(2)R.
why does ehattheta = sinthetaehat -cpsthetaehatn work for the projection vectors but ehattheta = costhetae^t-sinthetae^n does not work (this vector gives me the opposite magnitudes of the correct answers)?