| Problem statement Solution video |
DISCUSSION THREAD
Discussion and hints:
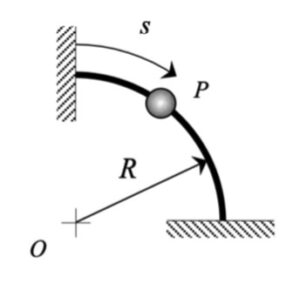
Here, the distance traveled along the circular path, s, is known as an explicit function of time. The speed of P at any instant is simply v = ds/dt, and the rate of change of speed is: v_dot = d2s/dt2. Since the path is circular, the radius of curvature is given by: ρ = R. With these three quantities, you have everything that you need to write down the velocity v = v et and a = v_dot et + (v2/ρ) en.
Carefully watch the animation below of the motion of P. When the acceleration vector shown in RED points “backward” from the direction of travel, particle P is slowing down; that is, the rate of change of speed is negative. Conversely, when the acceleration vector “forward” of the direction of travel, P is increasing in speed with a positive rate of change of speed. You will see that the period of time during which the speed of P is increasing is rather short, occurring during a time immediately after the direction of P changes.
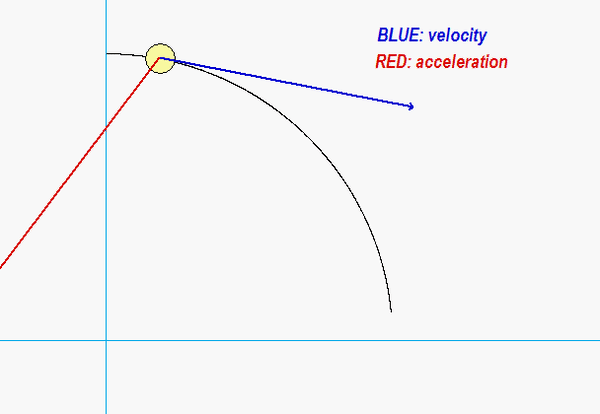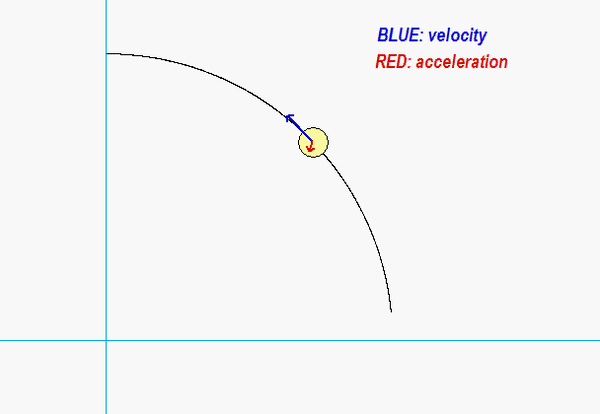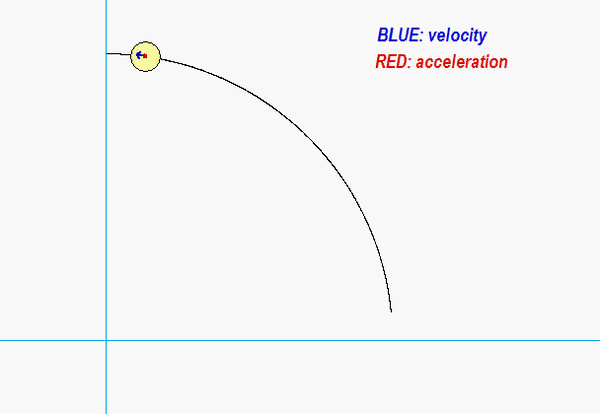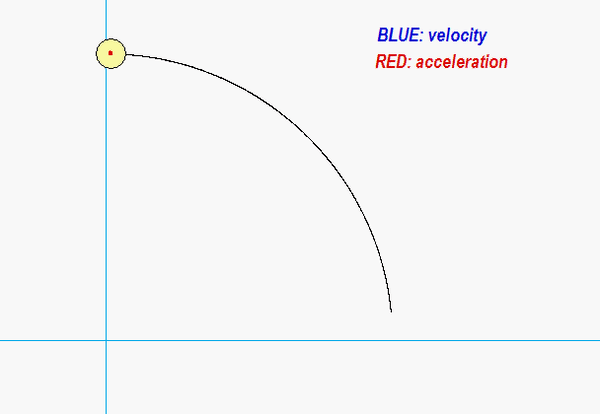
Any questions??
When we sketch the acceleration vector, are we supposed to sketch 2 different vectors? One in the et direction and one in the en direction? or are we supposed to sketch them as one combined vector?
One combined vector with two components.
When it asks to show the position of P, do we just need to draw it along the circular path or does it want us to calculate the distance from the left of the path in radians or something else?
We are asking for just a sketch of where P is at that instant. Calculate the value of “s” and determine where along the path that location is. Make of sketch of the quarter circle, showing roughly where P is. At that location, show e_t and e_n, along with v and a., again as sketches.
Can we leave our solutions in terms of e^c where c is a constant or should we use a calculator to solve for exact values? Also if we do solve for exact values how many significant figures should we use?
You may leave your answers in terms of “e”.
When drawing the acceleration vector, would they like us to draw one arrow, or sketch two acceleration arrows in their respective et and en components?
We are looking for a single vector. If you want to identify the two components (tangential and normal) of the vector, in your sketch that might be helpful.
I am struggling to find the et and en unit vectors. Is there a formula or assumption to find the angle for the vector equations?
The et unit vector is tangential to the path of motion, which means it is in the same direction as the velocity. The en unit vector is normal (90 deg) to the et vector. For a circular path it points inside the circle.
Is v dot the same thing as s double dot? It’s the last thing I need for finding the a vector
The speed v is equal to s_dot. So, yes, v_dot = s_ddot.
I don’t think that you solve for them, you write the answer in terms of them. In cartesian coords you do i _hat and j_hat, and for this coordinate system those are the labels for the values correlating with the tangent and normal components instead of x and y components. Correct me if I’m wrong!
this was meant as a reply to Krishnasanhith Choppara
Do we have to sketch a new quarter circle for the a part to show the position. I calculated s and just stated the value of s in the existing sketch with unit vectors e_n an e_t will that do?
Using the existing sketch is fine.