Homework H1.C – Sp 26

10 Comments
Problem statement
Solution video

DISCUSSION THREAD

Discussion and hints:

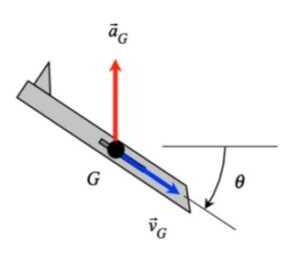
In this problem, we know both the magnitude and direction for each of the velocity and acceleration vectors for the center of mass G. We know that the unit tangent vector et is in the same direction as the velocity vector vG. The unit normal vector en is perpendicular to et, and points “up and to the right” (do you know why?). Projecting the acceleration vector aG onto the unit tangent and unit normal vectors gives us the information that we need to find the rate of change of speed and the radius of curvature of the path.

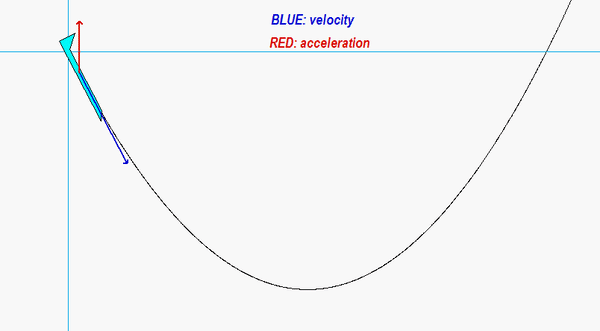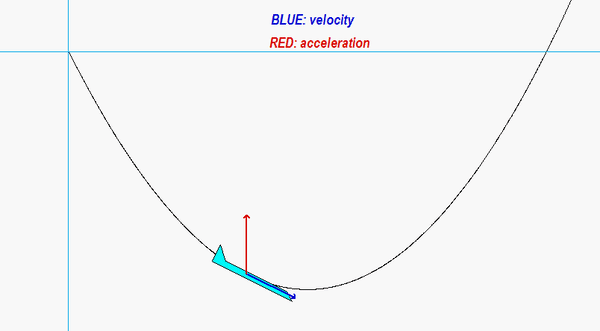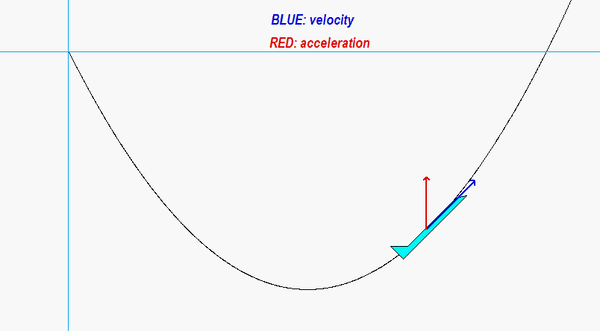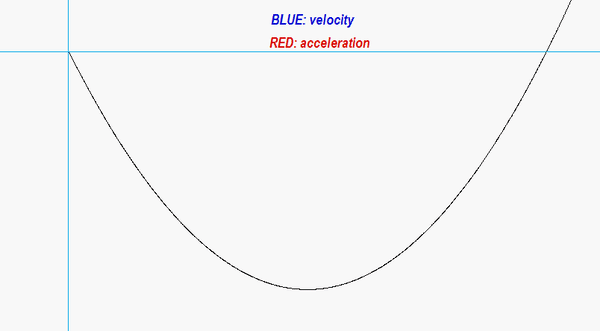
Carefully watch the animation below of the motion of the aircraft. When the acceleration vector shown in RED points “backward” from the direction of travel, the aircraft is slowing down; that is, the rate of change of speed is negative. Conversely, when the acceleration vector is “forward” of the direction of travel, the aircraft is increasing in speed with a positive rate of change of speed. If you follow this logic, you are on your way to understanding the usefulness of the results of the path description of kinematics!

Any questions??

10 thoughts on “Homework H1.C – Sp 26”

  1. If the rate of change of speed is negative when the aircraft travels downwards, and the rate of change of speed is positive when the aircraft travels upwards, is there an instant where the rate of change of speed is 0?

    1. I was thinking that if the above is true, then we could use the magnitude of acceleration equation to solve for the radius of curvature, which would hold true for other values of vdot if the path were a circle. Is there a better way to think about this?

      1. My recommendation is to consider the projection of the acceleration vector onto the e_t and e_n directions.
        * The projection of a onto e_t is equal to v_dot.
        * The projection of a onto e_n is equal to v^2/rho.

        That gives you two equations for two unknowns. Solve.

        1

    2. You are asking a good question.

      As discussed about the DISCUSSION section, the rate of change of speed is negative on the downward portion of the path, and the rate of change of speed is positive on the upward portion of the path. The transition from negative to positive rate of change of speed occurs at the bottom-most point on the path. You can see that from the animation because at that point the acceleration vector in red is perpendicular to the velocity vector, as it should be when v_dot = 0.

      Does this help?

      1

  2. little confused on the wording, when it says find rate of change of speed (b), i’m assuming the question wants a vector in path coordinates not cartesian right?

  3. Just a reminder on notation for acceleration.

    * The component of acceleration that is tangent to the path is known as the “rate of change of speed”, v_dot (as the name implies, it is the rate at which the speed is changing in time).

    * The component of acceleration that is perpendicular (normal) to the path tangent is known as the “centripetal” component of acceleration: v^2/rho.

    You are asked to find v_dot and rho. Based on above, you simply need to project the acceleration vector onto the e_t unit vector to find v_dot, and project the acceleration vector onto the e_n vector to find v^2/rho.

  4. Assuming that I completed the question correctly, one tricky part of the question I found that I originally performed the wrong process of was projecting the acceleration vector in the tangent direction of travel. While you are given the exact angle, you must pay attention to how it is provided on the question sheet – simply using cosine and sine immediately is not the right path – instead, make sure to check the angle between vector aG and the unit normal and tangent vectors to find the right projection values.

    1

Leave a Reply