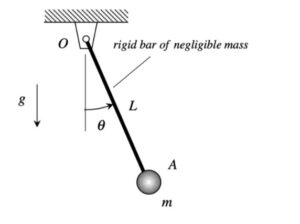
Discussion and hints:

The derivation of the dynamical equation of motion (EOM) for a system is a straight-forward application of what we have learned from Chapter 5 in using the Newton-Euler equations. The goal in deriving the EOM is to end up with a single differential equation in terms of a single dependent variable that describes the motion of the system. Here in this problem, we want our EOM to be in terms of θ(t).

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a FBD of the particle. It is recommended that you define and use a set of polar coordinates for this problem.

Step 2: Kinetics (Newton)
Write down the Newton equation for the particle in the θ-direction.

Step 3: Kinematics
Do you need any additional kinematics for this problem?

Step 4: EOM
Step 2 should produce a single differential equation in terms of the dependent variable θ. Note that this EOM contains a nonlinear term of sinθ. Recall that we can represent the sine function by its power series representation: sinθ = θ – θ³/3! + θ⁵/5! – …    For small angles θ, we see that this series could be approximated by its leading term, giving: sinθ = θ. The approximation for small angles of oscillation produces a LINEAR differential equation. Use this approximation here.

Any questions?