| Problem statement Solution video |
NOTE: Please use θ = 30* when solving.
DISCUSSION THREAD
Any questions??
DISCUSSION
In some sense, this is a very standard kinematics of rigid bodies problem. A rigid link connects points A and B. To relate the motion of these two points, you will need the following kinematics equations:
vA = vB + ω x rA/B
aA = aB + α x rA/B – ω2 rA/B
The nuance in this problem is the acceleration of point A. From what we learned earlier in the semester, the acceleration of a point can be written in terms of its path coordinates; that is, here the acceleration of A can be resolved into its tangential and normal components. As you proceed on this problem, you first need to recognize the tangential and normal unit vectors, et and en, for the motion of A. Then write down the acceleration of A, first in its path components, and then in its Cartesian component. In the end, you will have two scalar equations coming from the rigid body acceleration equation in terms of two unknowns.
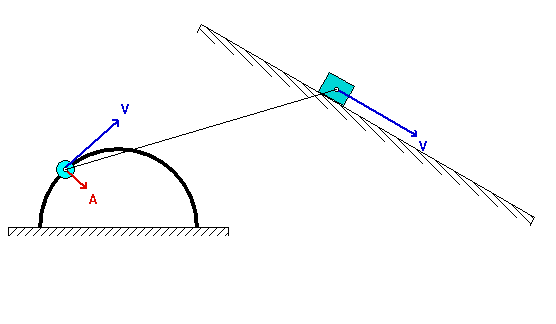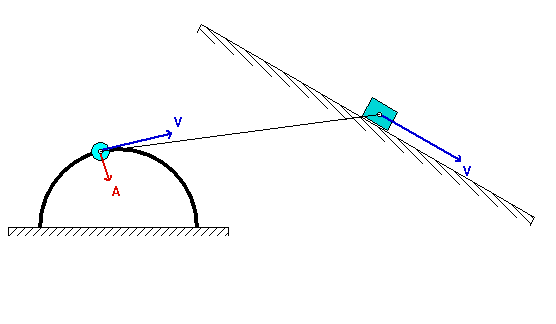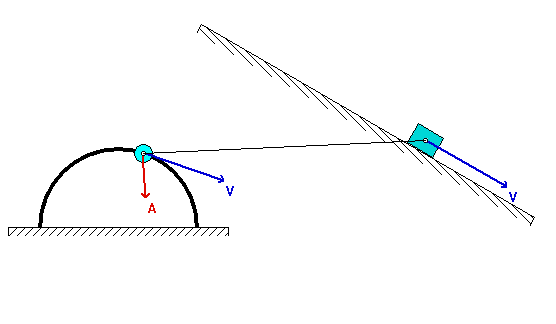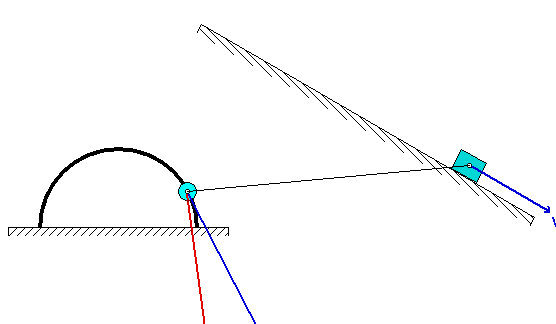
How are you supposed to do this problem w/o the value for theta? Should answer’s be in terms of theta? Does it cancel out?
Please use theta = 30°.
Apologies for the omission.
Before this comment was made, I already solved the Homework using Cos(theta)=0.8 and sin(theta)=0.6. Do I have to resolve and resubmit with theta=30?
Your choice of theta will be fine.
Do we need to quantify the location of the instant center, or can we just eyeball the location of the instant center with perpendicular lines to the velocities?
Please use a graphical construction to locate the IC. Use a straight edge to draw the perpendicular lines that are needed in locating the instant center.
Should we, for the IC of AB, consider the way it is drawn in the diagram or use the actual numbers? I’m confused because the length discrepancy between L and R, where h is longer than R despite R being larger, will result in widely varying answers.
The numerical values for the parameters of the homework problems vary from term to term when the problem is being used.; however, we do no re-draw the figures every time the problem is used. Treat the image provided as a sketch and not a scale-drawn figure. You cannot use the image for measuring distances; you would need to use the number provided.
For Part c), this is somewhat of a moot point. All we are asking for here is to use the location of IC to verify the DIRECTION of travel for the particle A.