Homework H2.C – Sp 26

11 Comments
Problem statement
Solution video

DISCUSSION THREAD

Ask your questions here. And, consider answering questions of your colleagues here. Either way, you can learn.

DISCUSSION and HINTS

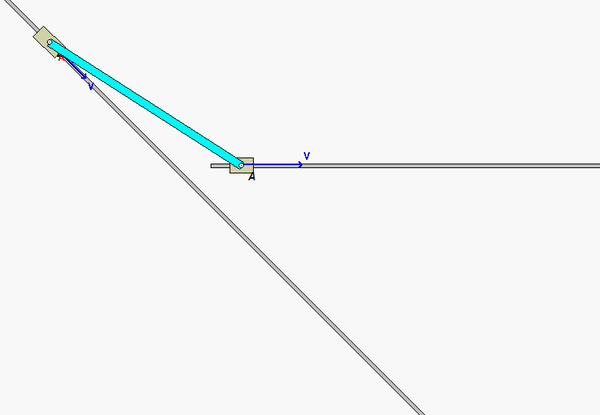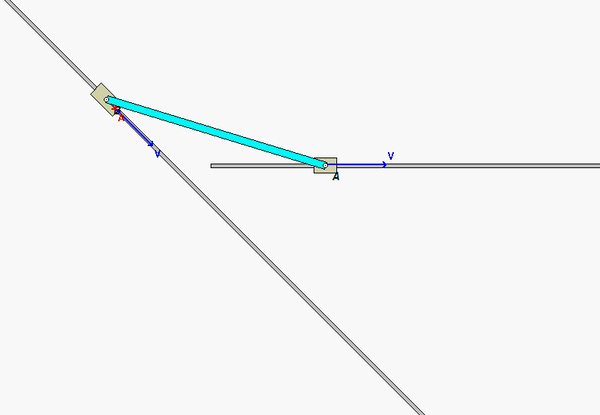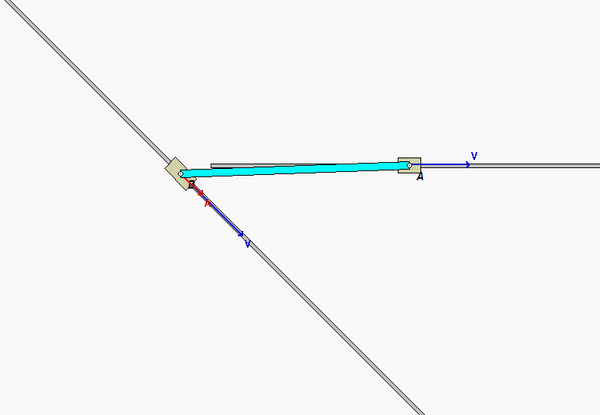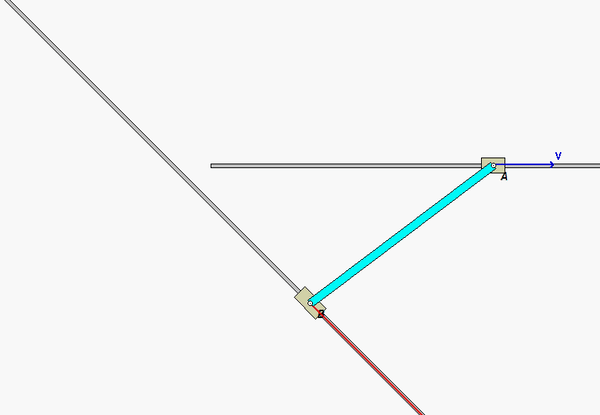
In this problem, end A of the bar is constrained to move along a straight horizontal path with a constant speed of vA, whereas end B is constrained to move along a straight, angled path. As you can see in the animation below of the motion of the bar, the speed of B is NOT a constant (the acceleration of B is non-zero, and is, in fact, increasing as B moves along its path).

In your solution, it is recommended that you use the rigid body kinematics equations relating the motion of ends A and B:

vB = vA + ω x rB/A
aB = aA + α x rB/A – ω2rB/A

For these equations, you know: i) the magnitude and direction for the velocity of A; ii) that the acceleration of A is zero (constant speed along a straight path); and, iii) the direction for the velocity and acceleration of B. These two vector equations produce four scalar equations that can be solved for four scalar unknowns: vB, aB, ω and α.

 

11 thoughts on “Homework H2.C – Sp 26”

  2. I found it to be very beneficial in this problem to ensure your have the correct signs on your velocity and acceleration vectors for B. The animation posted on the blog is very helpful for this.

    1. Please note that you do not need to know the directions for v_B and a_B a priori. You can assume a direction and let the math tell you if that assumed direction was correct.

  3. When solving for omega using the angle phi, do you have to reconsider the directions for the ratio between vB in the x and y direction before plugging in the know values as B is moving to the right and down? Or do you simply plug in the scalar values of vbx and vby?

    1. Just to clarify, I mean (vby/vbx) = tan(45). As the bar appears to be moving down, would it be -tan(45) as one of the components acts in the negative direction?

      1. The way that you handle the angle of the guide for particle B is to write the velocity of B in the following vector form:

        v_B = v_B*(cos(phi)*i_hat – sin(phi)*j_hat)

        where v_B (not bold) is the unknown speed of B.

        You do the same thing for the acceleration of B.

  4. I have separated v_B into the two components in the i_hat and j_hat direction but I am not sure how to solve for the missing values. Would I just rearrange each equation for omega and set the two equal?

Leave a Reply