Homework H1.I – Sp 26

5 Comments
Problem statement
Solution video

DISCUSSION THREAD

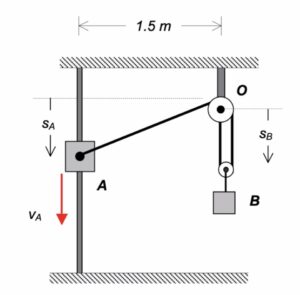
Discussion and hints:

This is a typical cable-pulley problem for us in this course. Here, we need to first write the length of the cable, L, in terms of the position variables of sA and sB, along with some constants. Since it is assumed that the cable does not break, go slack or stretch, the length L is constant. Take a time derivative of the expression above for L. This relates the speeds of blocks A and B.

Carefully study the animation of the motion of this cable-pulley system provided below. One of the questions asked of you is the speed of B when sA = 0. What do you see in the animation below as sA passes through zero? Does your equation above tell you the same thing?

 

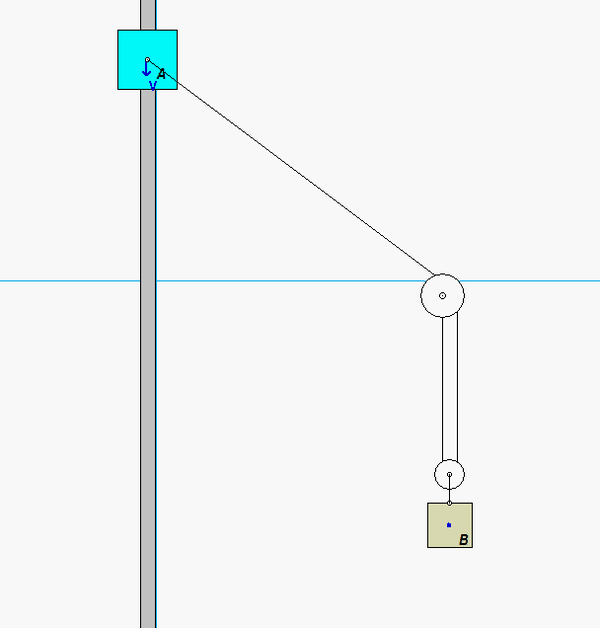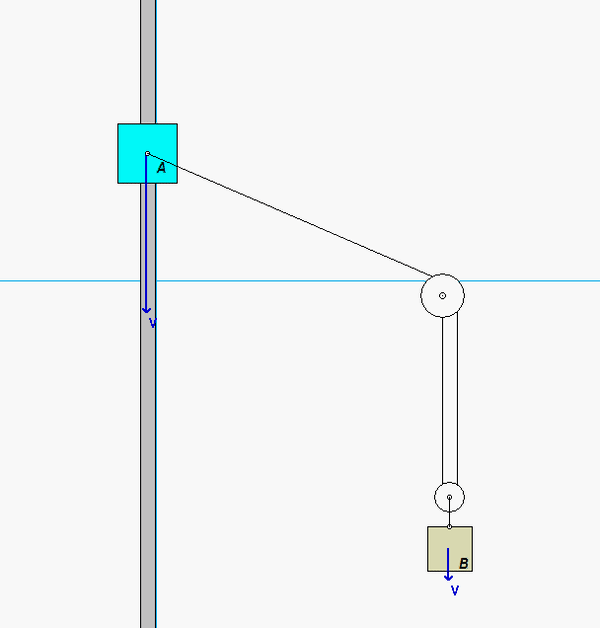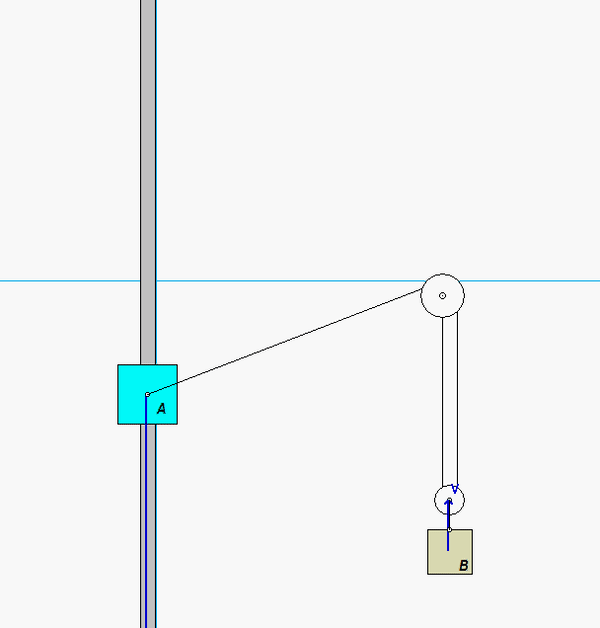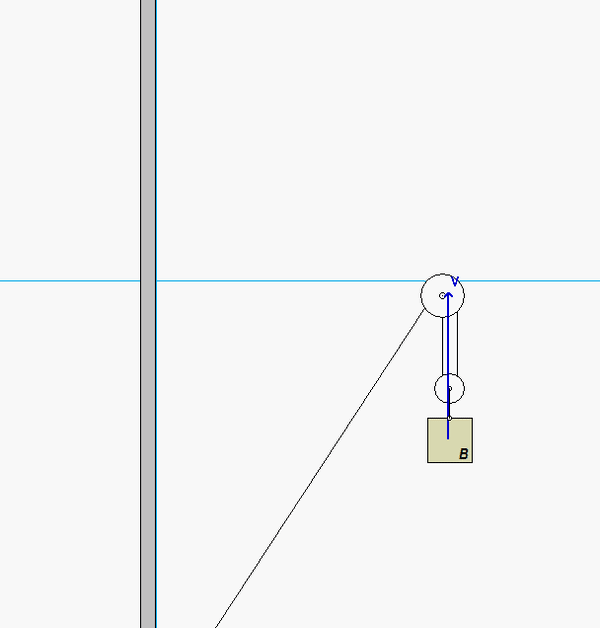
Any questions??

5 thoughts on “Homework H1.I – Sp 26”

  1. The hints indicated that 2vA < vB; is this only the case for the animation shown or the actual problem provided to us? When I calculated the speed of vB for sA = 4m, I obtained a different result that doesn't represent the hint's statement.

  2. I think the animation above is a little backwards of how it is labeled in our specific problem. In particular, block A and block B are swapped. This means that in our problem, I believe the hint should read 2vB<vA. That does end up being true.

    1. To Aiden and Matthew: The discussion for the wrong problem was originally included with this discussion post. This has now been corrected. Thanks for pointing out the mistake.

      Apologies for the confusion created by this errant post.

  3. Hi I have a question regarding my process. When you take that derivative of the square root when solving for VB do you have to multiply an additional SA by the SA dot which is the derivative of SA since it’s just the chain rule or is it just the SA dot multiplied by the 1/2(\sqrt) ^-1/2, so like 1/2(\sqrt)^-1/2 * SA dot * SA or 1/2(\sqrt)^-1/2 * SA dot. I may have just made a tiny error. Any help would be appreciated.

    1. Suppose that you want to take the time derivative of the function sqrt(sA^2 + h^2):

      d/dt(sqrt(sA^2 + h^2)) = (1/2)*(sA^2 + h^2)^(-1/2)*(2*sA*sA_dot)

      The last term in this expression (the one about which you are asking) arises from the chain rule.

Leave a Reply