| Problem statement Solution video |
DISCUSSION THREAD
Discussion and hints:
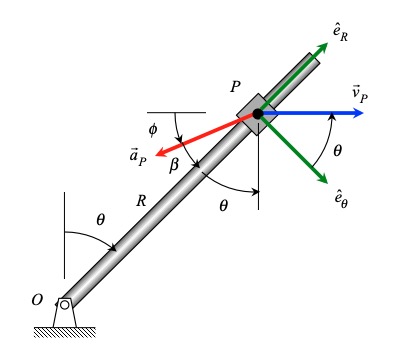
For the polar description to be used here, the radial unit vector eR points from O toward P. The transverse unit vector eθ is perpendicular to eR and points in the direction of increasing angle θ (clockwise from eR).
The solution of this problem comes down to trig – can you do the projections of vP and aP onto the polar unit vectors eR and eθ ? For example, the velocity of P can be written as vP = vP sinθ eR + vP cosθ eθ. And, the acceleration of P can be written as aP = –aP cosβ eR – aP sinβ eθ . No formulas to remember, just look at the figure and do the trig! From these results, you can identify the time derivatives of R and θ.
Any questions??
The wrong image and description are posted here; it seems like H1.E was accidentally reposted as H1.F here on the blog. The problem for H1.F is attached to the link though.
It is now fixed. Thanks for pointing out the error.
When solving for part b, should we convert to from polar to cartesian systems and then solve for each component using a system of equations? Could there be an easier alternative to this? I have heard of others utilizing the projections of vectors for velocity and acceleration, but we have not been taught this in class.
Cameron,
Please review the discussion provided above on the solution process. This process is to first project the velocity and acceleration vectors onto the polar unit vectors e_R and e_theta. (Note that the results of those projections are provided to you above…use those results to check your answers.)
Then note that:
v = R_dot*e_R + R*theta_dot*e_theta
a = (R_ddot – R*theta_dot^2)*e_R + (R*theta_ddot + 2*R_dot*theta_dot)*e_theta
Comparing these these two sets of vectors, you can balance terms to get equations for the four unknowns.
Does this help?
Yes, thank you
Hello. I am also a bit confused on how to exactly go about this process, because I understand this involves trigonometry, but I can’t quite wrap my head around the exact process on finding the Beta angle using the theta of thirty degrees. There needs to be a couple steps to this process, because once we use the trig then we can use the velocity and acceleration equations to solve for the unknowns, right? I am just a bit confused on where to start. Any help would be greatly appreciated.
From the figure: theta + beta + phi = 90°. You know values for theta and phi. Therefore, you can find beta.
The discussion above provides you with the vectors representing velocity and acceleration in terms of speed and magnitude of acceleration through the angle of theta.
You also know the two fundamental equations for velocity and acceleration in terms of R, R_dot, R_ddot, theta_dot and theta_ddot.
Balance out the coefficients of the e_R and e_theta for these two coefficients, and you have four equations and four unknowns.
Does that help?
Thank you so much for your help!
I don’t really understand the signs on the acceleration. Is it because the vector is pointing towards the third quadrant? Thanks
The signs on the components of a vector have only to do with the projection of the vector onto the e_R and e_theta unit vectors. They are not directly connected to horizontal or vertical directions.
The velocity vector is pointing in both the positive e_R direction and in the positive e_theta direction. Hence, both components are positive.
The acceleration is pointing in both the negative e_R direction and the negative e_theta direction. Therefore, both components are negative.
Could we instead use phi to find the acceleration components? A bit difficult to wrap my head around using beta.
Yes, beta is the only angle that you need to find the acceleration components.; however, you need to use theta and phi to find the numerical value for beta.
For velocity, the only angle that you need is theta. That is the way that it is described in the Discussion section above.