| Problem statement Solution video |
DISCUSSION THREAD
Discussion and hints:
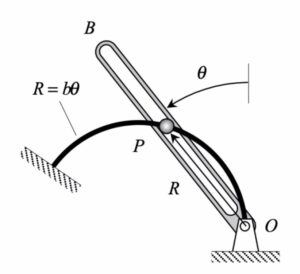
For the polar description to be used here, the radial unit vector eR points from O toward B. The transverse unit vector eθ is perpendicular to eR and points in the direction of increasing angle θ (counterclockwise from eR).
The first time derivative of θ is given to the the constant ω. Therefore, the second time derivative of θ is zero. The time derivatives of R are found from direct differentiation of the path equation R = bθ . These results then are used to find the vP and aP in terms of their polar coordinates.
Carefully watch the animation below of the motion of P. As we have seen before, the velocity vector is always tangent to the path, whereas the acceleration vector has both tangent and normal components. The normal component always points inward to the path. Also, as we have seen before, when the angle between vP and aP is less than 90°, the speed of P is increasing. As you can see from the animation below, the speed of P is increasing throughout the entire motion.

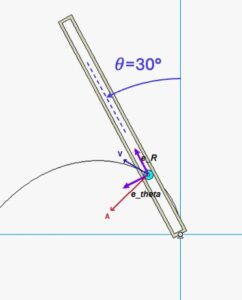
Please note the orientations and directions of the polar unit vectors eR and eθ shown in the figure below for θ = 30°.
Any questions??
Because the theta is represented by rad/s, does this mean implicit differentiation isn’t used for solving for R_dot as R =b(theta) would be in the time domain?
True. In this case implicit differentiation is the same as simply taking a derivative of R with respect to time directly.
Is the direction of positive theta fixed as going from left to right like the example from the lecture? Or is it based on what they give you in the drawing as the starting point for theta?
Please note the sign convention for the angle theta defined in the figure for the problem statement: theta is measured positive in the CCW direction from the upward vertical axis. The position for theta = 30° is shown in the above freeze-frame of the animation. Note the direction of the unit vector e_theta shown in this position based on the sign convention for the problem.
The direction of theta is based on the drawing so it should be from right to left based on the diagram.
Given that the equation for R is inches multiplied by radians, would the units for R be inches?
Since a radian is dimensionless, b*theta will have the same units as b (inches).
Is there any adjustments to the base velocity or acceleration equations because of the new orientation about the “y” axis. Or is the theta just arbitrary because all the other functions are in reference to it? In the lecture book we have the derivations of a and v but they have a sort of alignment with the positive x being the theta 0.
The velocity and acceleration equations are valid regardless of the choice of definition for the angle theta. That is, theta can be measured from any fixed reference line in the plane, and with theta being measured positive in either the CW or CCW direction. It is up to you to define your choice of angle, and for you to draw the e_R and e_theta unit vectors that are consistent with your choice of angle theta and observation/reference point O.
For this particular problem, theta is measure positively in CCW direction from the positive vertical axis. As always, e_R point outward from O toward point P, and e_theta is perpendicular to e_R in the direction of positive theta.
When finding velocity the e_r component is given by theta^dot, which means it is given in rad/s. Since we do not know the radius of the circle we cannot convert to inches/s. The e_theta is given by dr/dtheta * dtheta/dt which works out to in/s. Since we cannot convert one to the other, what units should we use for the final velocity answer? I am not sure we can assume that the path has a constant radius so finding r(pi/2) / 2 would not work.
I’m confused about how to find the r derivative. If it’s taken with respect to t, would that not make it 0?