| Problem statement Solution video |
DISCUSSION THREAD

Discussion and hints:
In this problem, one simply needs to differentiate both the x- and y-coordinates once with respect to time in order to find the corresponding Cartesian components of velocity. Taking another time derivative of each then produces the Cartesian components of acceleration.
The results of this analysis are shown in the animation below. From this animation, we see that the velocity of the P (shown in BLUE) is always tangent to the path of P. The acceleration (shown in RED) is not quite so simple: it has components both tangent and perpendicular to the path; however, the component perpendicular to the path always points inward on the path. Both of these observations are consistent with what we see in the next lecture when we develop the expressions for velocity and acceleration in terms of their PATH components.
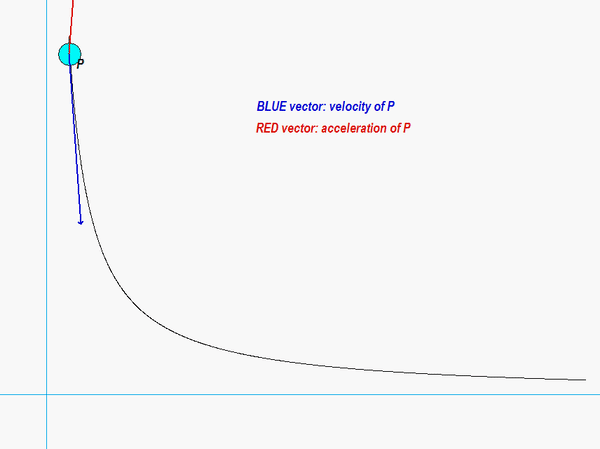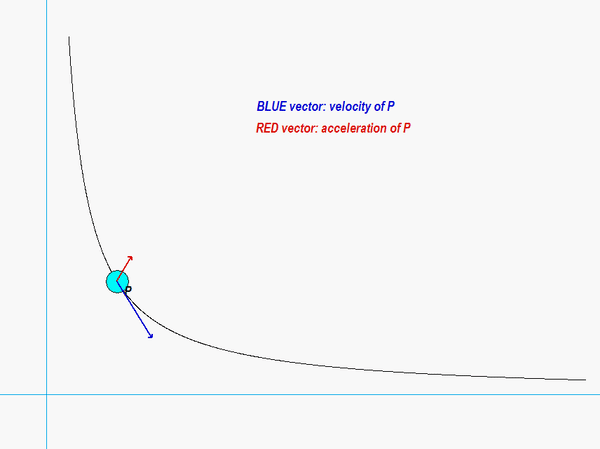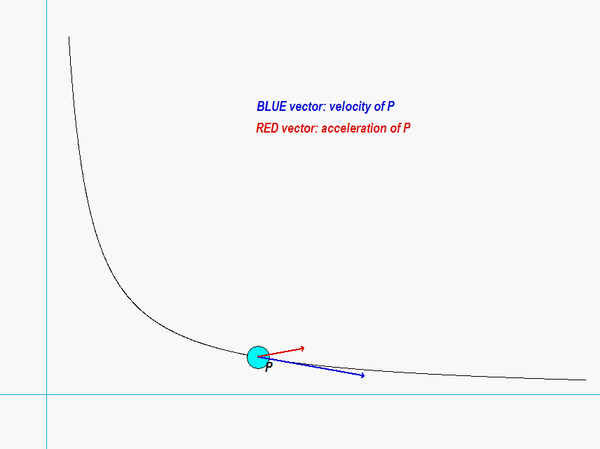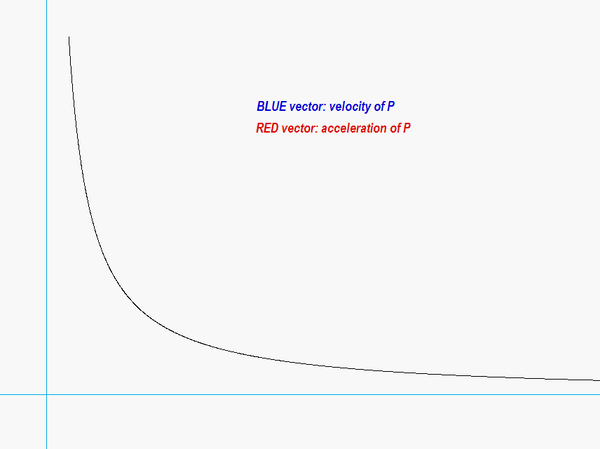
Any questions??
What does it mean that b=.5/s? Is a typo? If not, how do you interpret those units?
I think its supposed to mean “per second” or 1/s. That way the units in the exponent would cancel out.
As William points out, b needs to have dimensions of 1/time such that b*t = dimensionless. Since time is in seconds, then b has units of 1/seconds, as indicated in the problem statement. Similarly, c and h need to have dimensions of length and the same units as x and y, which are known to be in feet.
For the first part of the question, we are asked to find the path taken for the hyperbola in the xy-plane. I was looking through the textbook, but could not find how we are supposed to do that. I’m assuming it is a simple solution, but I’m not sure. Am I overthinking it?
The equation for a hyperbola with vertical and horizontal asymptotes is x*y = constant.