| Problem statement Solution video |
DISCUSSION THREAD
Discussion and hints:
In this problem, the xy-Cartesian components are constrained through the equation of the path of P: x2 + y2 = R2. The x-component of the position is an explicit function of time. Finding the time derivatives of x is done through simple time differentiation of x = b sinωt. The derivatives of y with respect to time is found through the time differentiation of the constraint equation: x2 + y2 = R2. Please review the examples worked out in lecture to assist you in this differentiation.
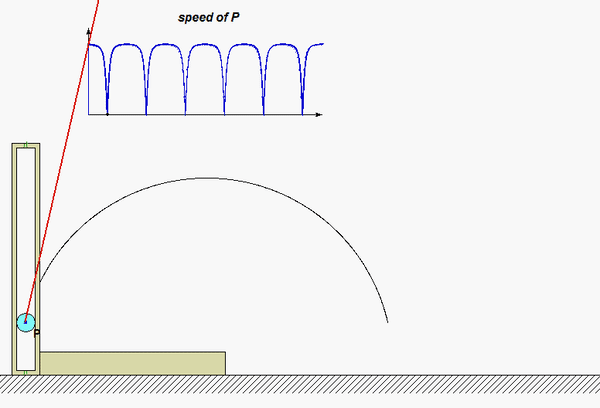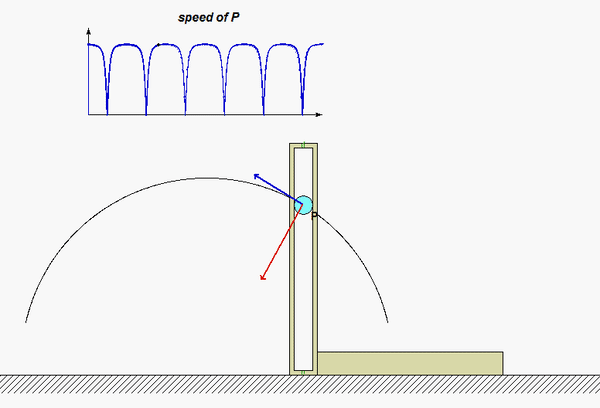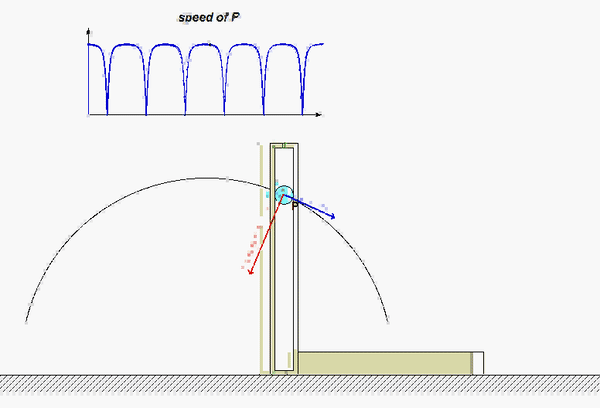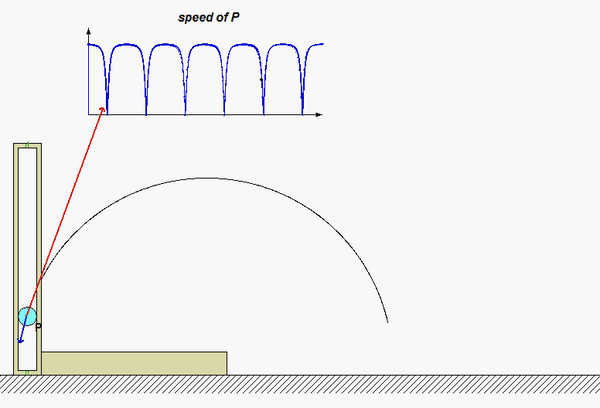
The results of this analysis are shown in the animation below. From this animation, we see that the velocity of the P (shown in BLUE) is always tangent to the path of P. The acceleration (shown in RED) is not quite so simple: it has components both tangent and perpendicular to the path; however, the component perpendicular to the path always points inward on the path. Both of these observations are consistent with what we see in the next lecture when we develop the expressions for velocity and acceleration in terms of their PATH components.
Any questions??
Before making your sketch for part a, calculate the position of the ball when t=0. The example sketch that was given does not match up with the given constraint of t=0. This will make the velocity and acceleration vectors make more sense when you have to go and draw them in at the end of the problem.
When solving for y in this problem (to then be used to solve for ydot and ydoubledot), we are given a solution with both + and -. I assume we need to eliminate one of the signs to get one solution but am unsure what logic to use to simplify. Would we just use the positive y value because our reference point is above the x axis?
You may choose either solution, + or -.
Yes, you should use the positive y value because the particle can not move below the x axis.
In terms of units, I converted rad/s into m/s and mm into m but if I’m checking my units right that gives m^2/s for velocity? I don’t think that’s right and was wondering if somewhere could help because I’m just a little confused
Since omega*t must be dimensionless and t is given to be in seconds, then omega must have units of 1/seconds, or equivalently, as rad/second (since radians are dimensionless). Also, since x, y and R are all in millimeters, then dx/dt and dy/dt will be in mm/s, and d^2x/dt^2 and d^2y/dt^2 will end up in mm/sec^2.
Does this help?
The example from “Dynamics: A Lecturebook — E1.A.1” is really helpful to set up the acceleration equation