| Problem statement Solution video |
DISCUSSION THREAD

Ask your questions here. Or, answer questions of others here. Either way, you can learn.
DISCUSSION and HINTS
In this problem, the excitation does not come from a prescribed force, but, instead, it arises from a prescribed displacement on one body in the system. The support B here is given a prescribed motion of xB(t) = b cosωt, where ω is the frequency of excitation. Our goal is to solve for the particular solution of the response. Shown below are animations of this forced response corresponding to two different frequencies: the top animation has ω < ωn, and the bottom animation has ω > ωn, where ωn is the natural frequency of the system. Can you see the difference between these two simulation in terms of the the phase of the response? Study both the time histories and the animation of motion.
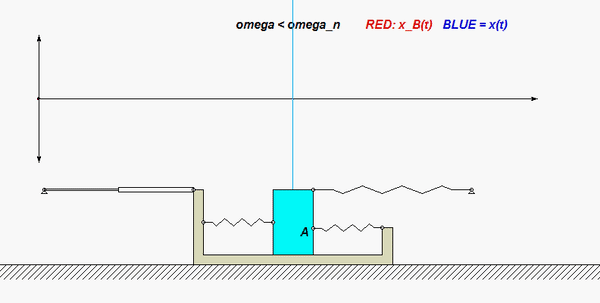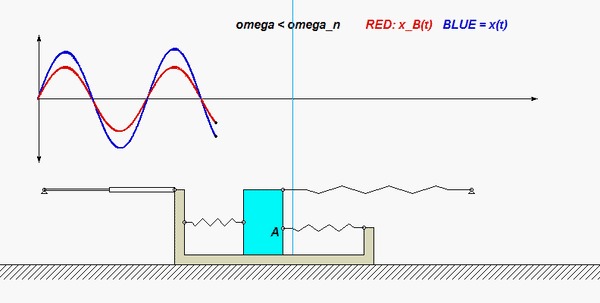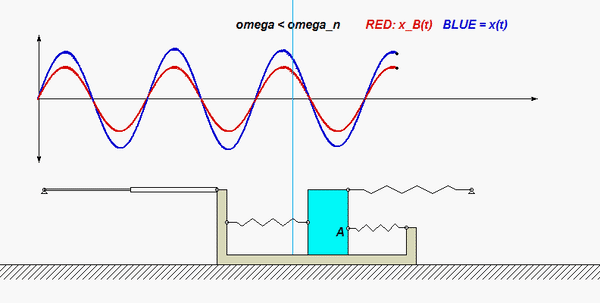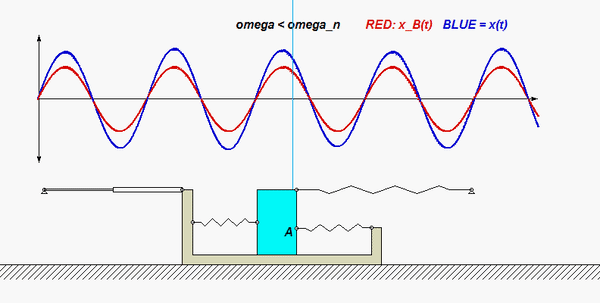
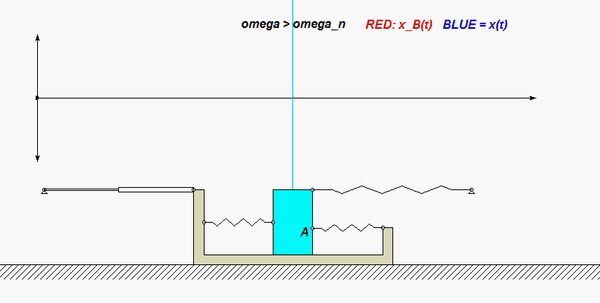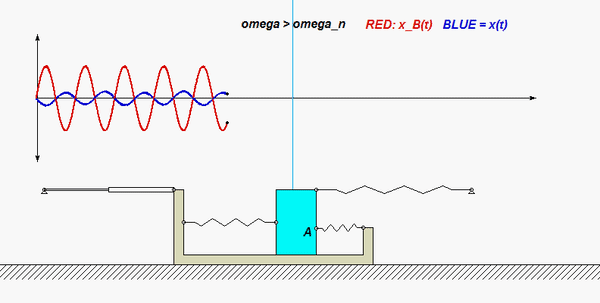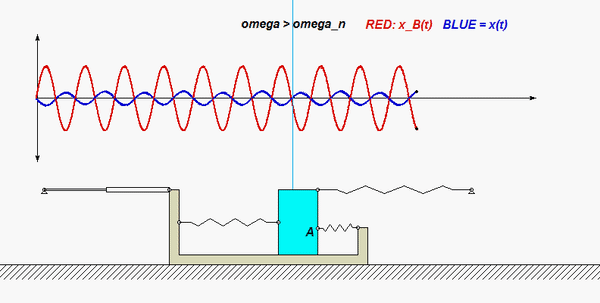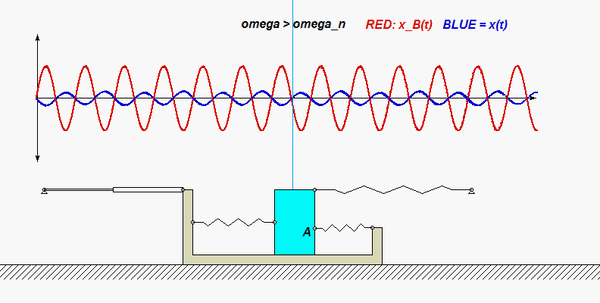
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
Draw a free body diagram (FBD) of block A. Take care in getting the directions correct on the spring forces acting on A. Note that you do NOT need an FBD of B since you already know its motion.
Step 2: Kinetics (Newton/Euler)
Use Newton’s 2nd law to arrive at the EOM.
Step 3: Kinematics
None needed here.
Step 4: EOM
The EOM was found back in Step 2.
Once you have determined the EOM for the system, identify the natural frequency from the EOM. From the EOM we know that the particular solution of the EOM is given by: xP(t) = A*sin(ωt)+ B*sin(ωt). How do you find the forced response coefficients A and B?
Does your result here agree with the expected relationship between excitation frequency and response with regard to the “phase” of the solution, and with the animations above?