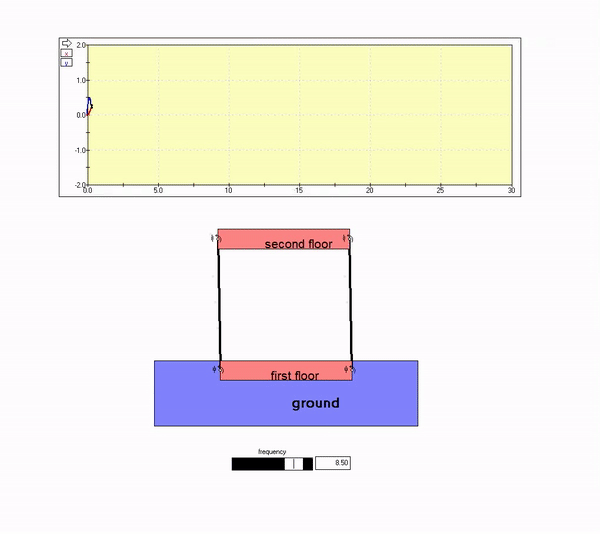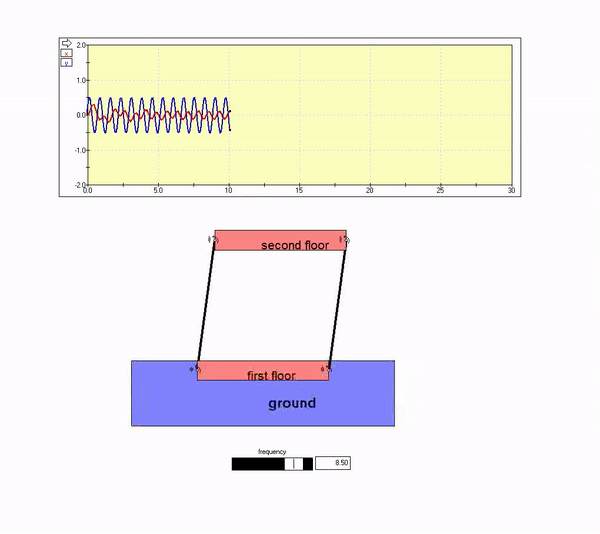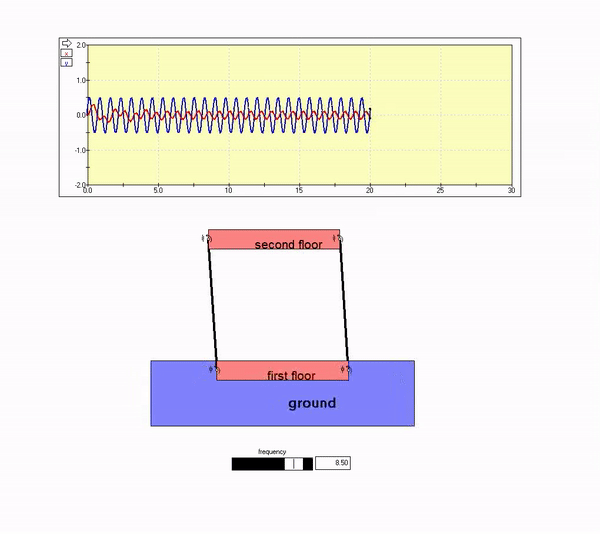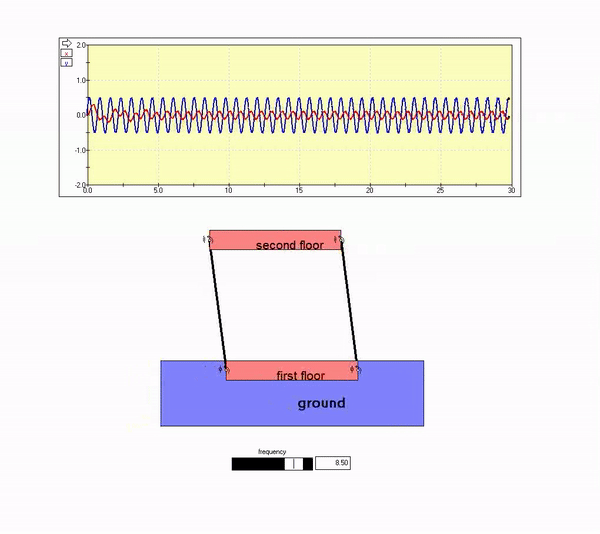
Consider the two-story building below that is experiencing horizontal ground motion.

Suppose that we model the building as a single-degree-of-freedom oscillator with ground motion y(t). Let m be the mass of the second floor and k be the side-to-side stiffness of the exterior sidewalls. The side-to-side motion, x, can then be represented by the following for harmonically time-varying ground motion.

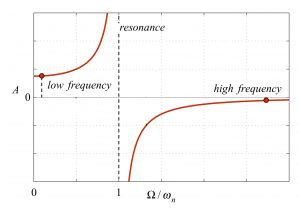
A plot of the steady-state amplitude of motion A is shown below as a function of the ground motion frequency Omega.
Let's consider several frequencies of ground motion, as described below.
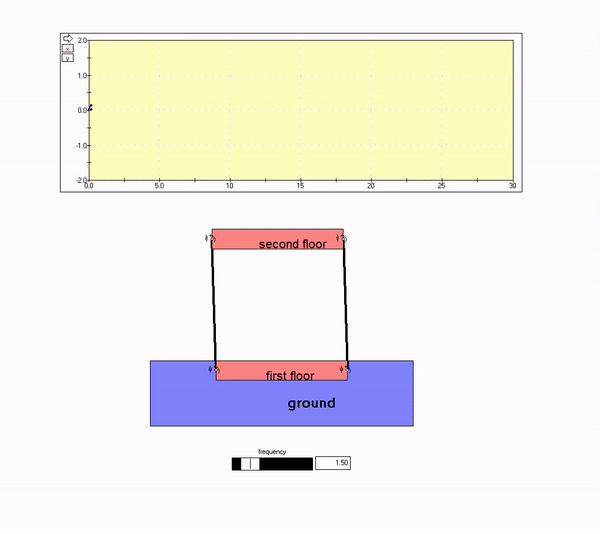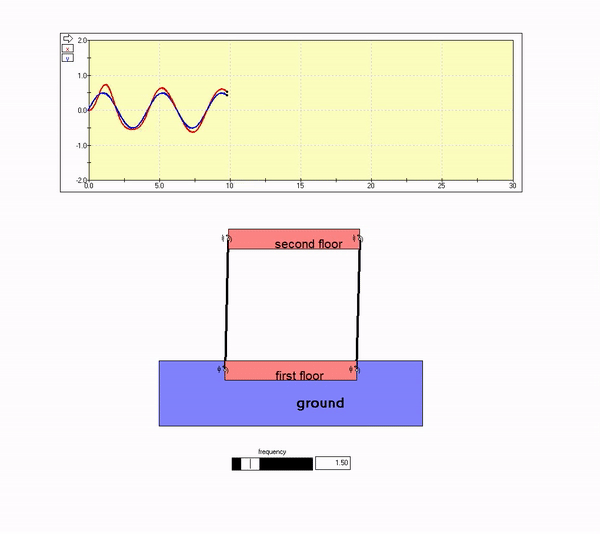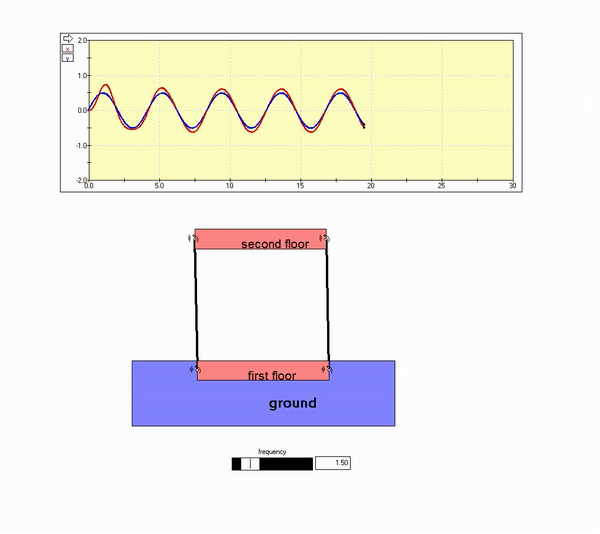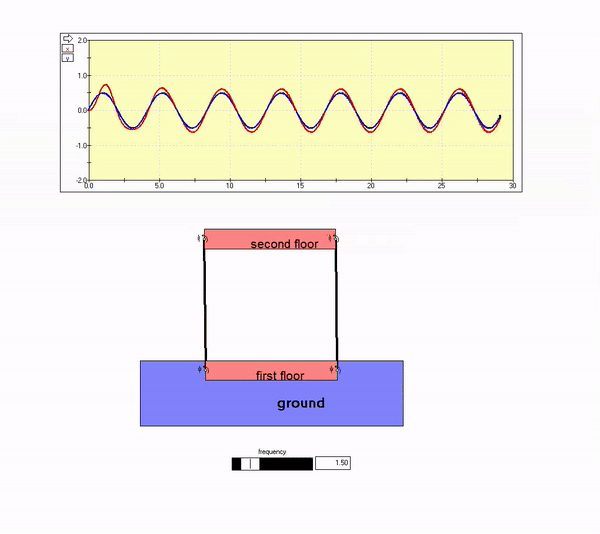
Low frequency ground motion
The plot above shows that the building response in-phase with the ground motion, with the amplitude of motion for the building being roughly equal to that of the ground. That is, the second floor motion effectively tracks the motion of the ground. This is seen in the animation below for Omega << omega_n.
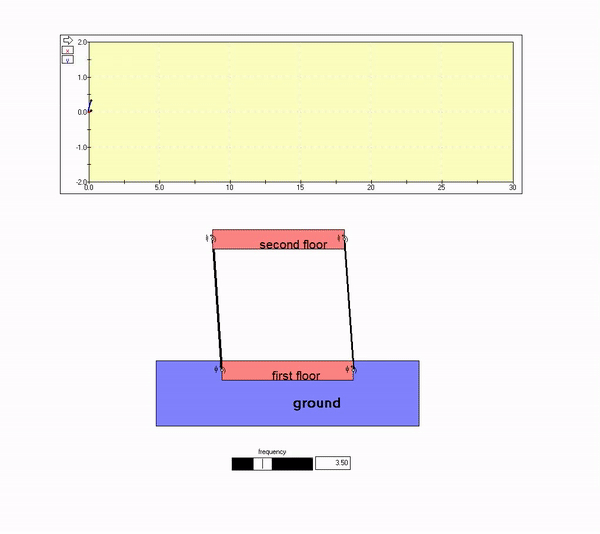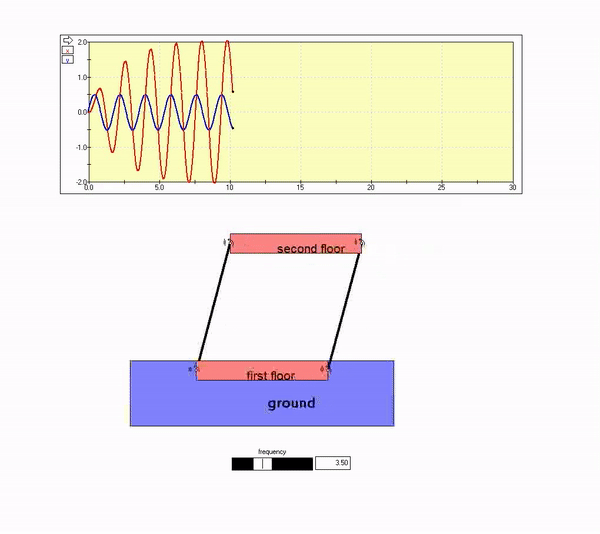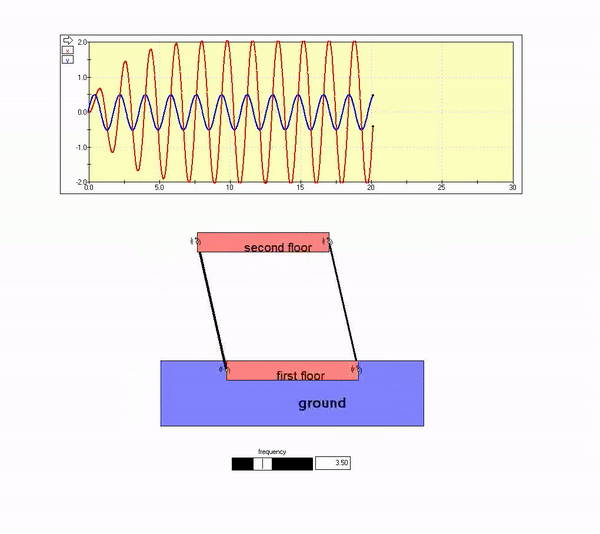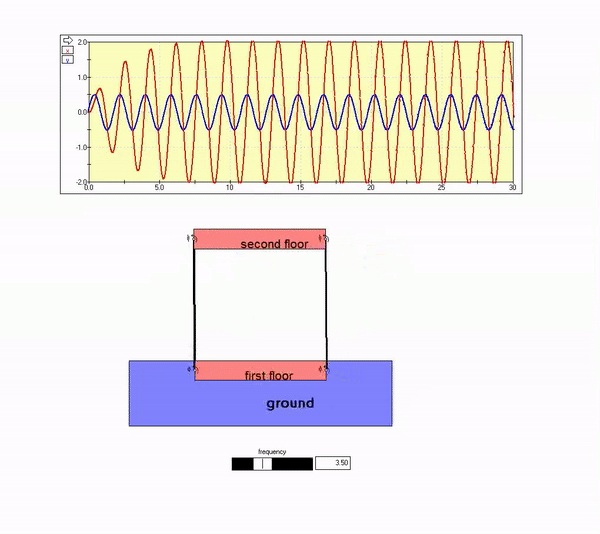
Ground motion frequency near resonance
With Omega near omega_n, the amplitude of steady-state response becomes large. This is as shown in the animation below.
High frequency ground motion
The plot above shows that the building response out-of-phase with the ground motion, with the amplitude of motion for the building being small as compared to that of the ground. That is, the second floor motion is nearly zero. This is seen in the animation below for Omega >> omega_n.