In your study of statics, you have learned that if forces act at only points points on a rigid body, then the resultant forces acting at these two points must be collinear in order for the body to be in equilibrium. This result is readily proved by using the equations of equilibrium for the body.
Here in this course in dynamics, the question may arise as to whether the collinearity of the forces still exists when the rigid body is not in equilibrium. The answer to this question, in general, is "no". As we have seen in dynamics, the summation of moments acting on the rigid body do not balance out, rather this summation is equal to the mass moment of inertia about the center of mass, IG, times the angular acceleration of the body, α. So if the angular acceleration of the body is not zero, and the mass moment of inertia about the center of mass is not zero, the collinearity will not exist.
Example
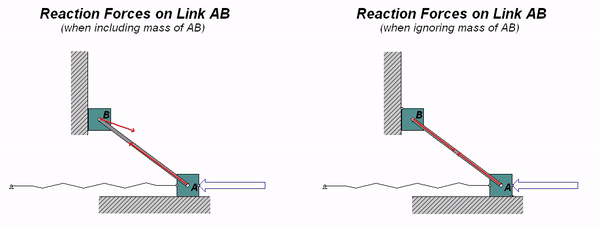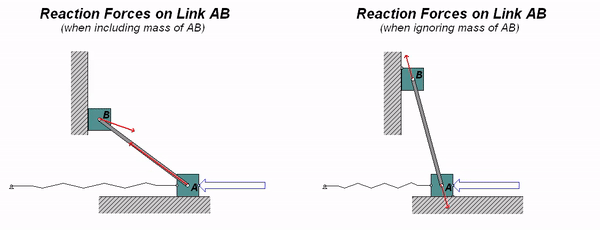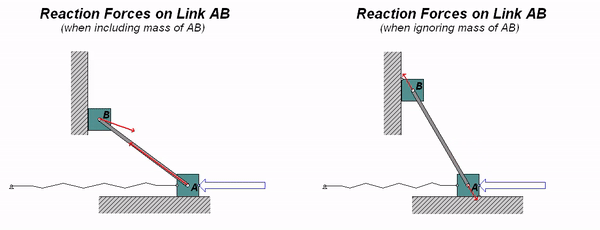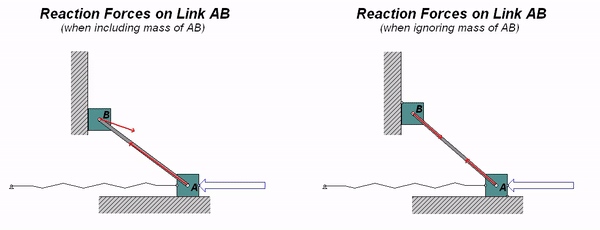
Consider the system shown below of two particles connected by a rigid body AB. If the mass of the bar is consider to be negligible, we expect the reactions at the ends of the bar to be collinear. If the mass of the bar is not negligible, we do not expect these reaction to be collinear.
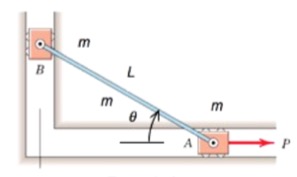
Watch the two animations below. The animation on the left was created from a simulation where the mass of AB is finite, and the animation on the right was created assuming that the mass of AB is negligible. As you can see, the collinearity of the reactions at A and B does not exist when we include the mass of the bar.