
A disk rolls on a stationary surface without slipping. In addition, the disk is in contact with a bar A on which it does not slip. The bar is moving to the right with a constant speed. What do we know about the motion of point B on the circumference of the disk?
Since the disk does not slip on the lower fixed surface, we know that B has ZERO velocity when it is in contact with that surface. Furthermore, the acceleration of B when in cannot with the stationary surface cannot have a component of acceleration tangent to that surface due to the no-slip condition. When B is in contact with bar A, we know that B has no acceleration in the direction of motion of the bar, again due to the no-slip condition with the bar.
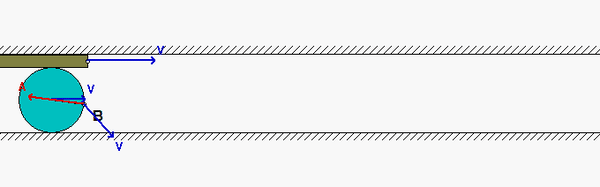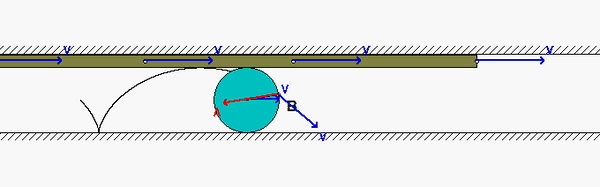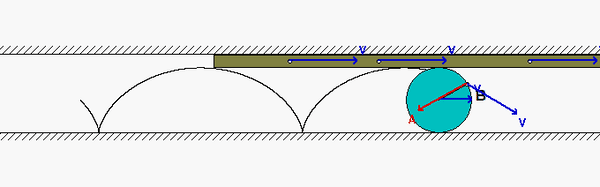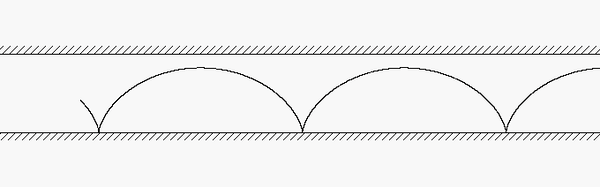
The animation above shows the motion of the system. Point B moves as we have described above, as it should. Note, also, that the speed of the center of the disk is exactly HALF of the speed of bar A. Do you know why? The acceleration of B always points toward the center of the disk - why?