Direct impact of pool balls
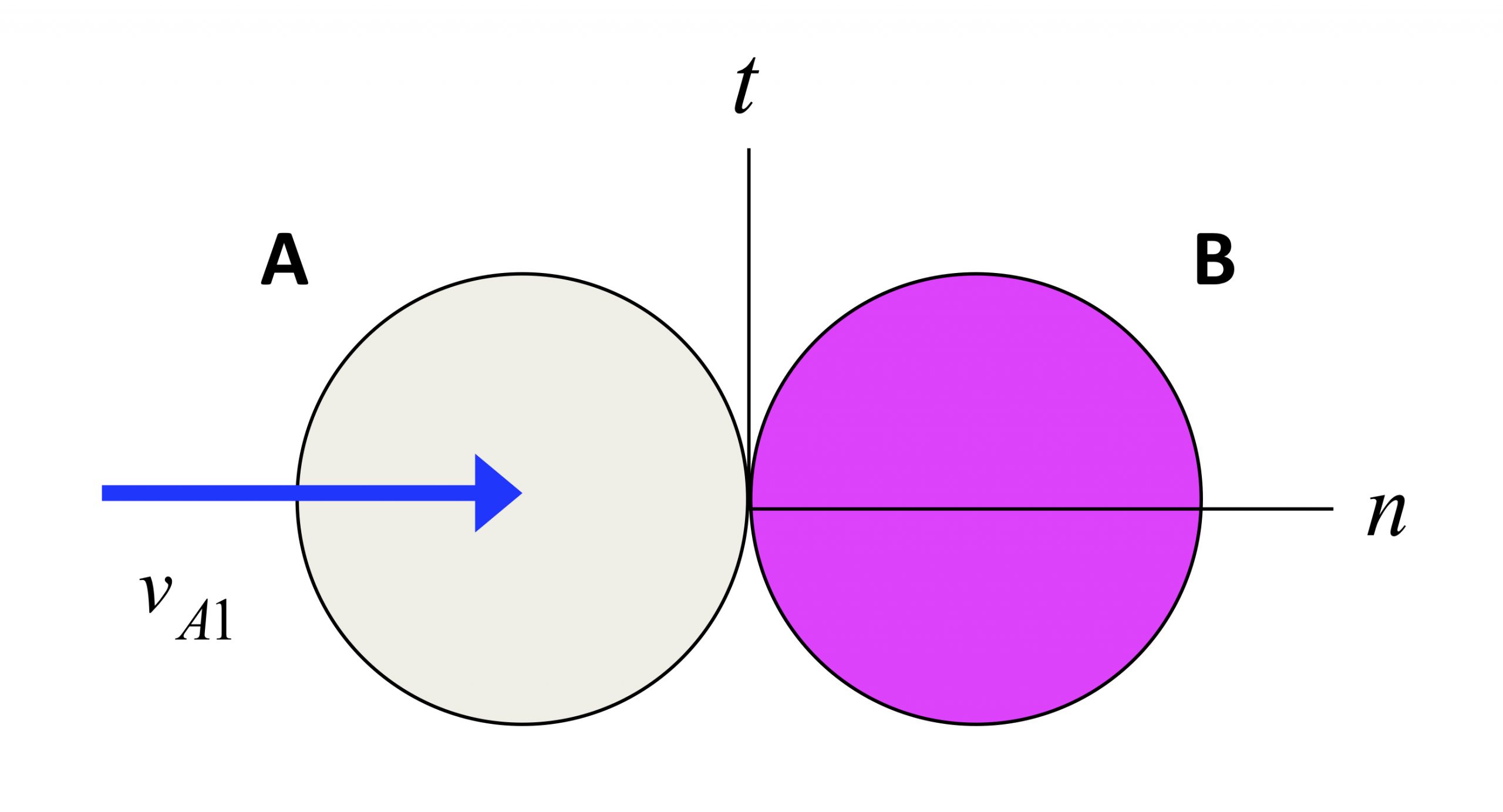
Ball A strikes a stationary ball B (with the balls having masses of mA and mB, respectively) with an initial speed of vA1, and with the velocity of A being directed at the center of ball B. The conservation of linear momentum in the n-direction for A and B together, and the coefficient of restitution (COR) give the following two equations:
mAvA1 = mAvA2 + mBvB2
vA2 = vB2 - evA1
The above equations can be solved for vA2 and vB2 for given values of masses and COR.
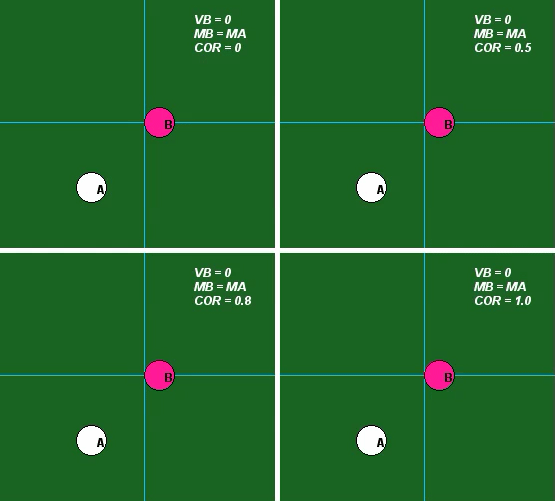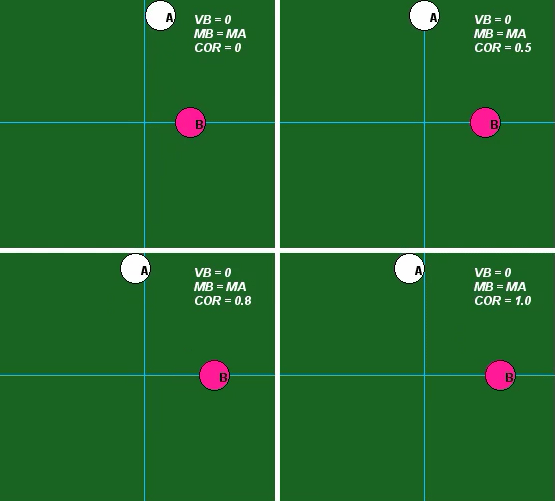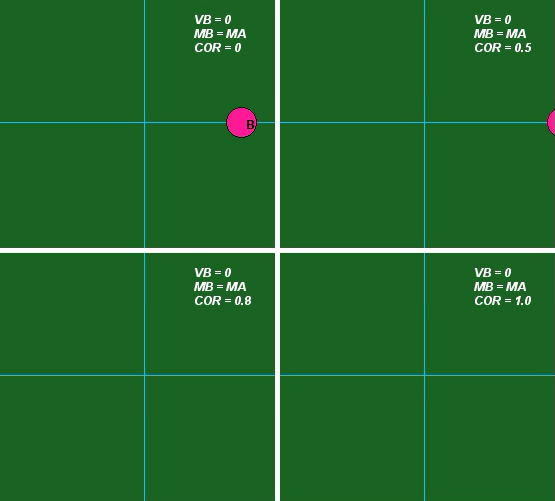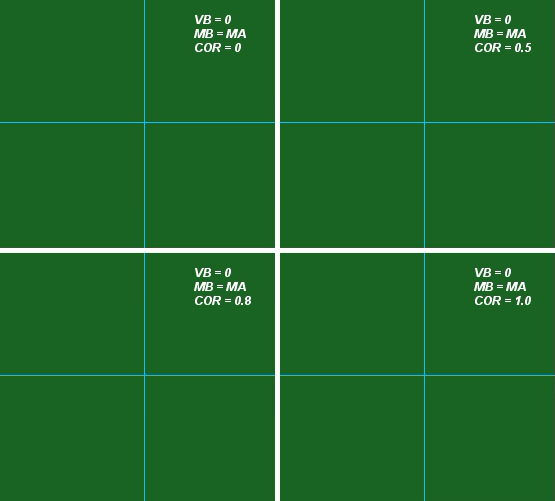
Influence of COR
The influence of the value of COR is demonstrated in the following set of four animations for mA = mB. Please observe the following from these results:
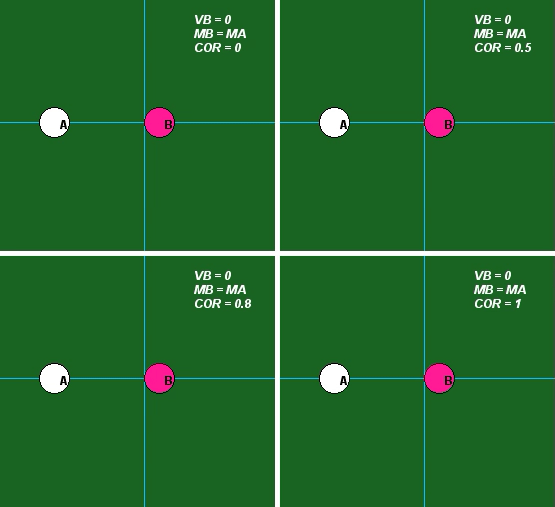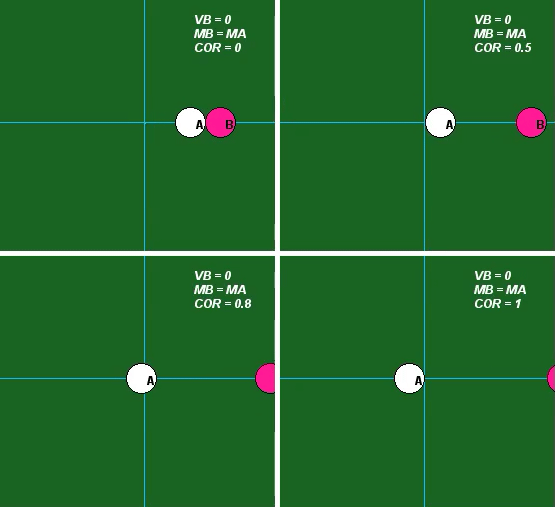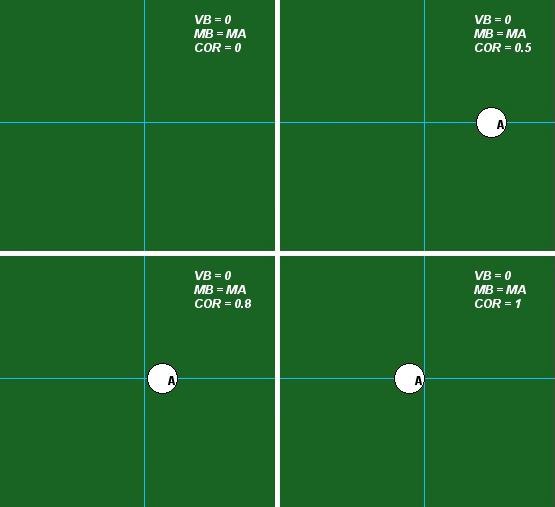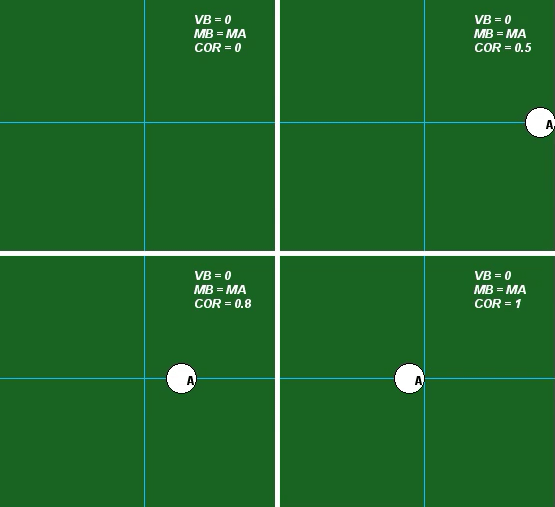
- For e = 0, we see that A and B stick together after impact. Is this consistent with the above equations?
- For e = 1, we see that A stops after impact. Is this consistent with the above equations? What is the speed of B after impact for this value of COR?
- For e = 0.5 and e = 0.8, we see that the speeds of A and B are between that found for e = 0 and e = 1 above. Is this consistent with the above equations?
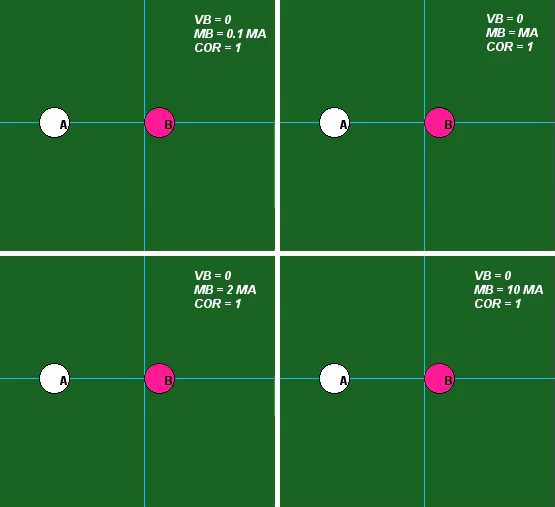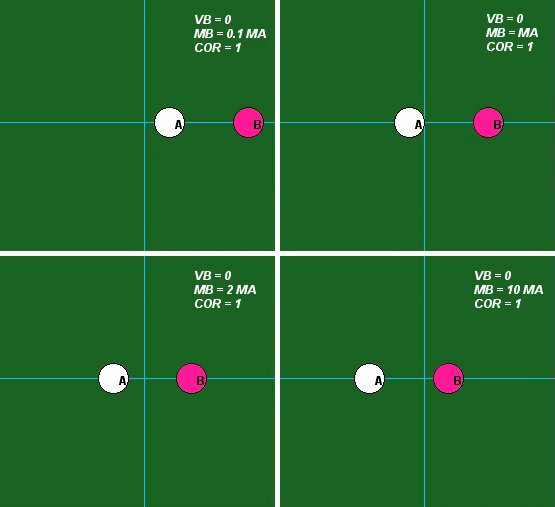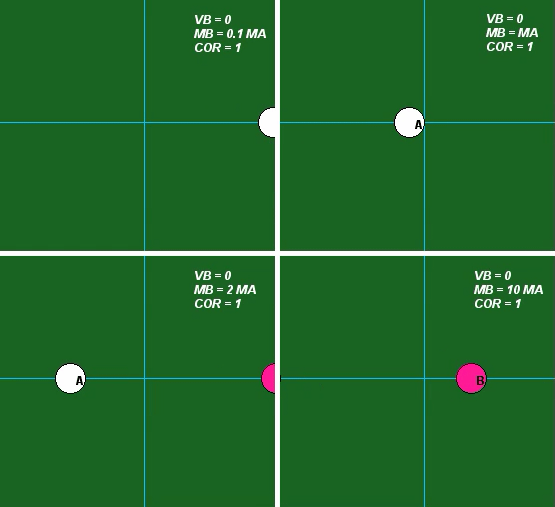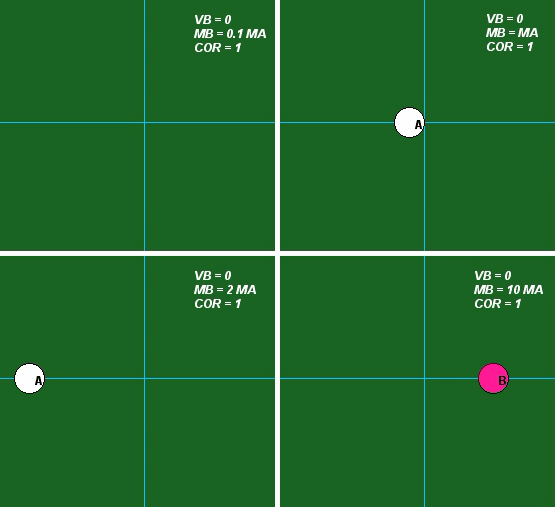
Influence of mass
The influence of the value of mass is demonstrated in the following set of four animations for e = 1. Do the animations below agree with the results of analysis using the above equations? Do they agree with your intuition?
Oblique impact of pool balls
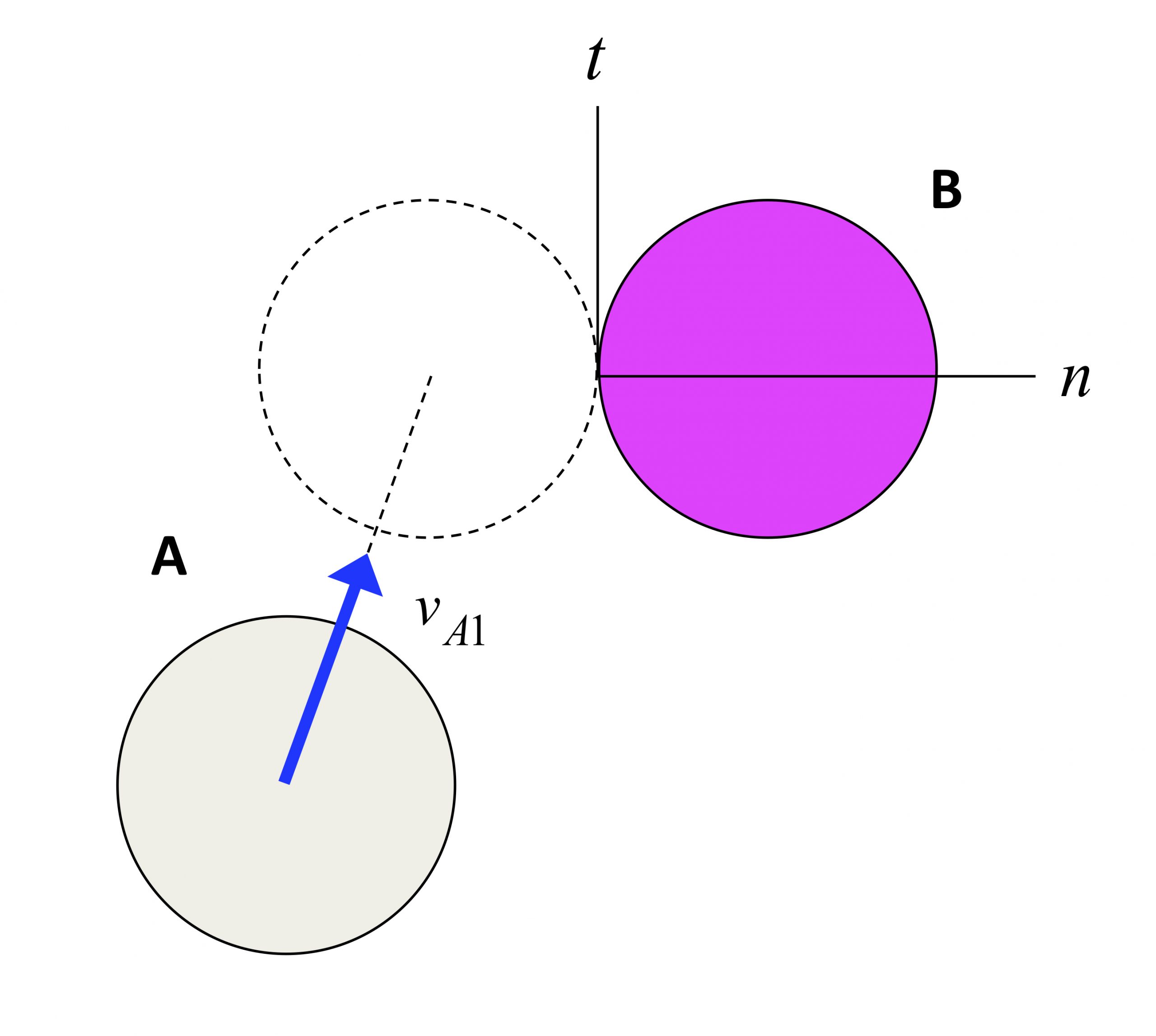
Ball A strikes a stationary ball B (with the balls having identical masses of m) with an initial speed of vA1, and with the velocity of A NOT directed at the center of ball B. The conservation of linear momentum in the t-direction for A and B individually, and in the n-direction for A and B together, along with the coefficient of restitution (COR) give the following four equations:
vAt2 = vAt1
vBt2 = vBt1 = 0
vAn1 = vAn2 + vBn2
vAn2 = vBn2 - evAn1
The above equations can be solved for the components of vA2 and vB2 for given values of COR.
Influence of COR
The influence of the value of COR is demonstrated in the following set of four animations. Are the results from the above equations consistent with that seen in the animations? Consider the two extreme cases of e = 0 and e = 1. Why do the two balls not stick for e = 0 as was seen in the direct impact case? Why does A not stop after impact for e = 1 as was seen in the direct impact case?