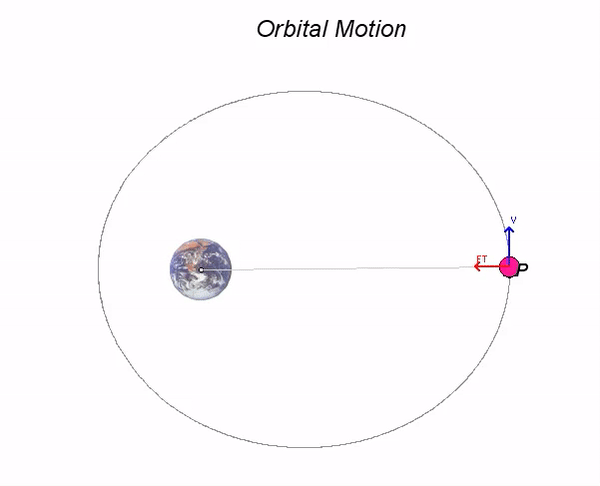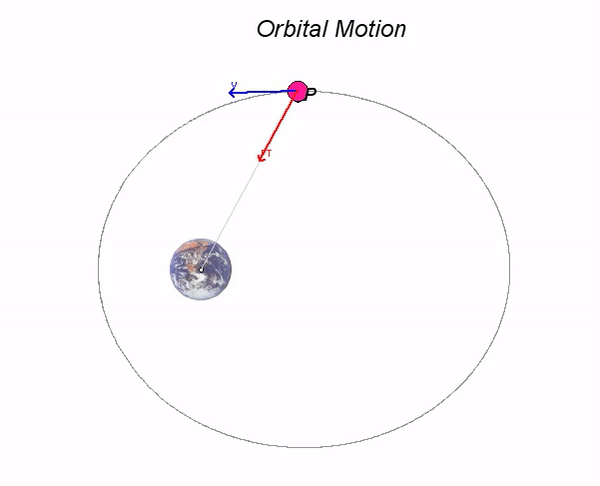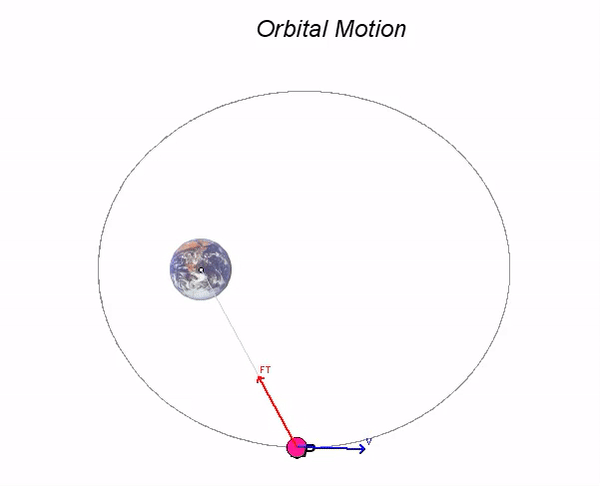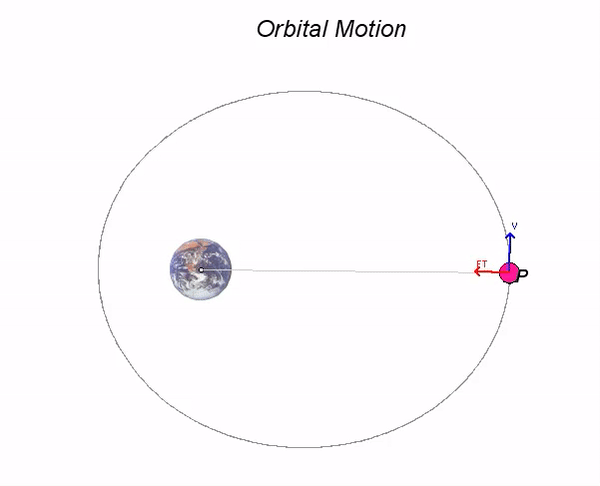
A satellite P is in orbit around the Earth. A gravitational attraction force Fgr from the Earth acts on the satellite, where:
![]() with G being the universal gravitational constant. For the instant shown, the velocity vP of the satellite makes an angle of θ with respect to the position vector rP/O.
with G being the universal gravitational constant. For the instant shown, the velocity vP of the satellite makes an angle of θ with respect to the position vector rP/O.

Observations and discussion
- Since energy is conserved (the gravitational force is conservative), we can use the work/energy equation to determine the speed of the satellite as a function of the distance R from O to P.
- Since the gravitational force Fgr is always acts along line OP, this force does NOT create a moment about point O. As a result, the angular momentum of the satellite about the center of the Earth is conserved (constant).
- What is the implication of conservation of angular momentum have on the observed motion of P? To see this, recall the definition of angular momentum:

- From this relation and the animation below, we see that when the satellite is at its closest position to the Earth (the position of minimum R is known as the "perigee" of the orbit), the velocity vector vP is perpendicular to rP/O (that is, sinθ = 1). From above, this says that the speed of P is a maximum at the perigee.
- Also, from this relation and the animation below, we see that when the satellite is at its furthest position to the Earth (the position of maximum R is known as the "apogee" of the orbit), the velocity vector vP is again perpendicular to rP/O (that is, sinθ = 1). From above, this says that the speed of P is a minimum at the apogee.
- For all other positions of P, there is a more complicated relationship between R and the speed of P. We need to look at both the conservation of energy and conservation of angular momentum in order to understand the satellite's motion. However, the motion of the satellite is completely described by those two equations. As you watch the motion of P below, look closely at the relationship among R, vP and sinθ - the product of these three terms is CONSTANT for all motion. Can you see this in the animation?
Kepler's 2nd Law
Kepler's second law states that the area swept out by the line connecting the satellite to the Earth's center over a given time Δt is a constant throughout the entire orbit of the satellite. See the animation below showing this swept area in blue (from Wikipedia).
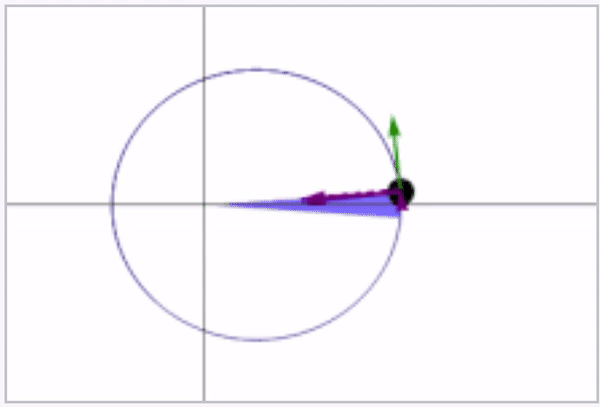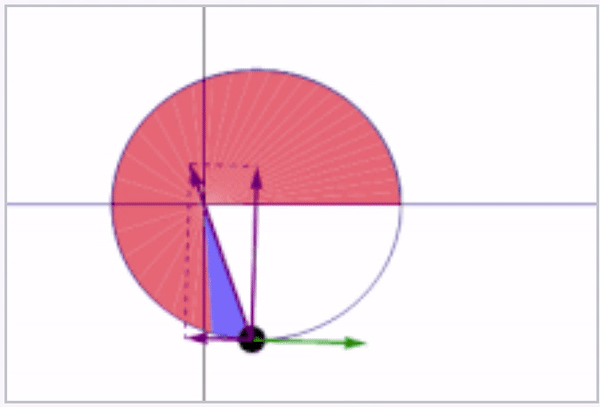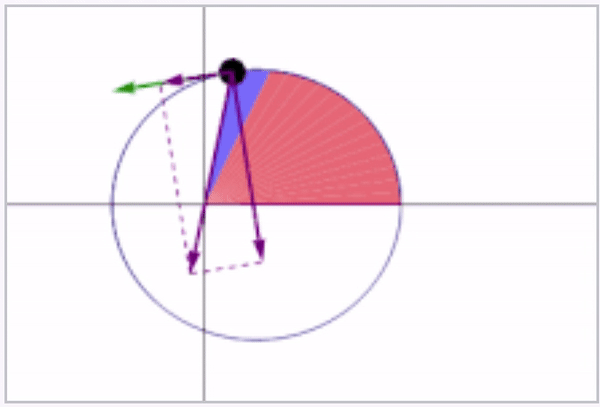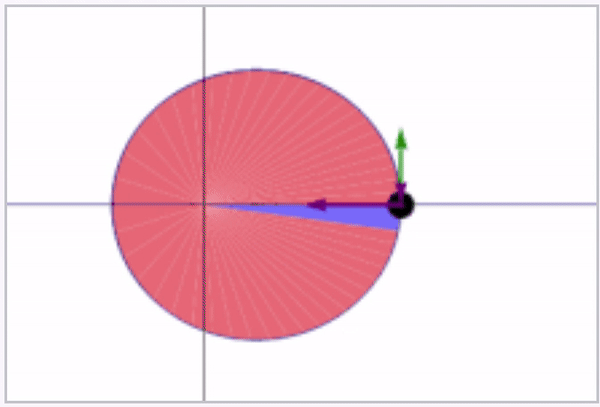
In addition to the blue swept areas, the green velocity vector is shown along with the acceleration in terms of its tangential and normal components (rate of change of speed and centripetal components) being shown in purple.
Freeze-frames of the above animation at two instants in time are shown below.
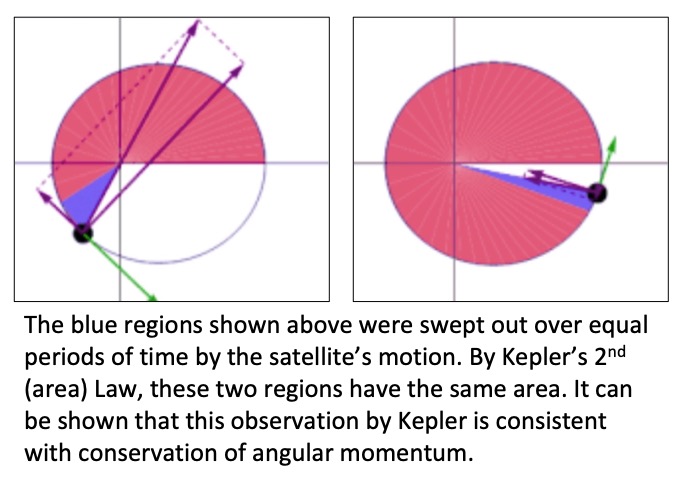
The consistency of Kepler's 2nd law with conservation of angular momentum is impressive considering that Kepler did this work in the early 1600's. This is compared with the time frame of Newton's work on his second law, the law of gravitational attraction and calculus from the late 1600's. Kepler was able to arrive at this second law without the benefit of Newtonian mechanics and differential calculus.