Consider a particle of mass m that is suspended in a vertical plane by a spring of stiffness k.
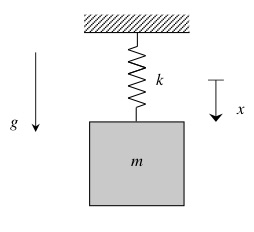
- When writing in terms of the x-coordinate measured from the unstretched position of the particle, the right-hand side of the equation of motion (EOM) includes the weight term, mg: m*x_ddot + k*x = mg, where x is measure positively downward.
- The static deformation, x_st, is found by setting x_ddot = 0, giving: x_st = mg/k.
- Motion about the static equilibrium state is described by the coordinate z = x - x_st. As seen in the lecture book, this produces a homogeneous EOM in terms of z: m*z_ddot + k*z = 0.
- Since the EOM in terms of z is homogeneous, the free oscillations are centered on the position of static equilibrium.
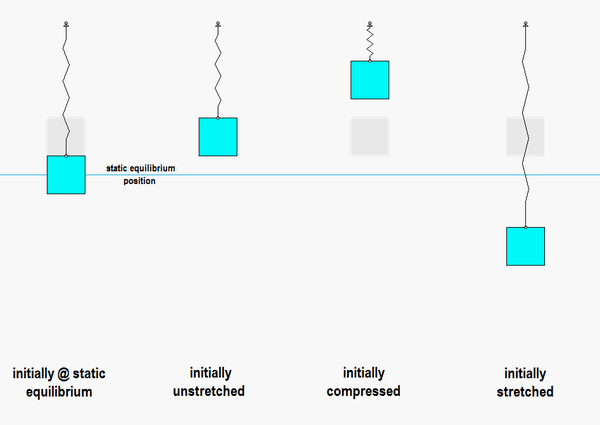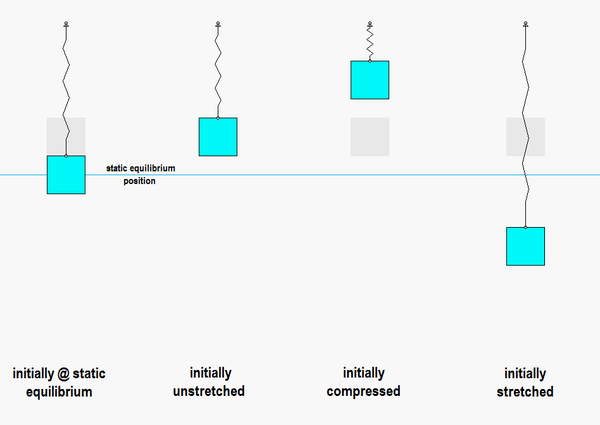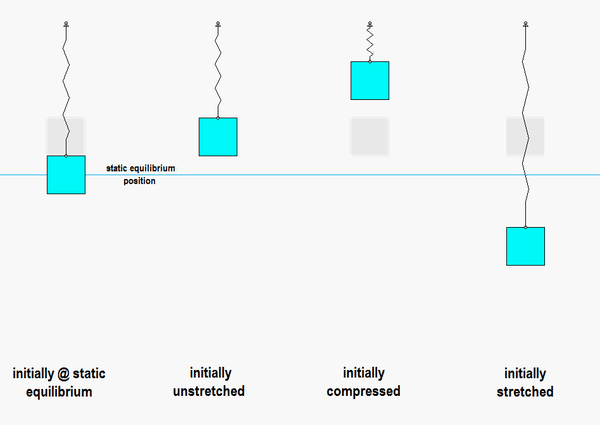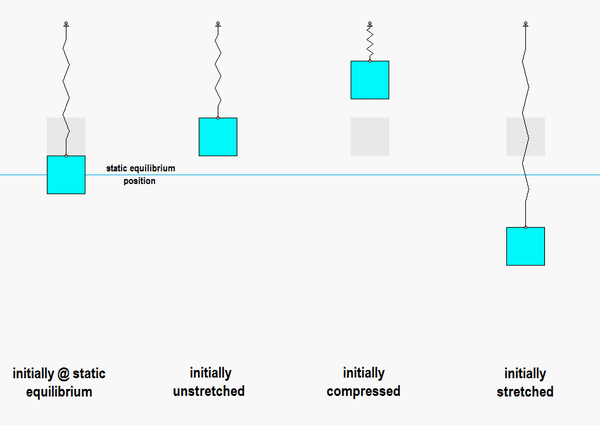
Consider the animation below:
- On the left is the response of the system if we release it from rest at the static equilibrium point: this produces no motion, as expected, since that is the position where the system remains at rest.
- In the animation second from the left, the block is released from a position where the spring is unstretched. In this case, the block has oscillatory motion centered on the static equilibrium point.
- In the animations third and fourth from the left, the block is released from rest with a general initial displacement: one with the spring compressed, and the other with the spring stretched. In both cases, the oscillations are still centered on the static equilibrium point.
- In all cases for which oscillations occur, the motions are centered on the static equilibrium point, and they all are of the SAME frequency of omega_n = sqrt(k/m). The amplitude of the motion is dictated by the amount of initial displacement from the static equilibrium point, NOT by the displacement from the unstretched state.