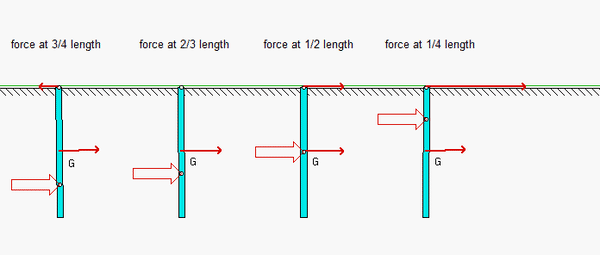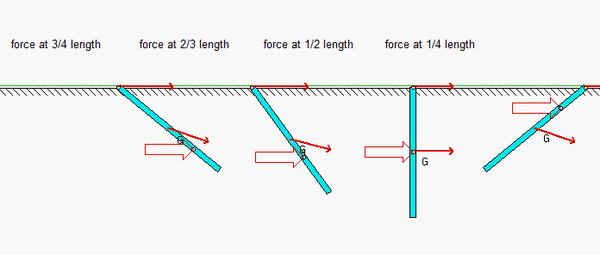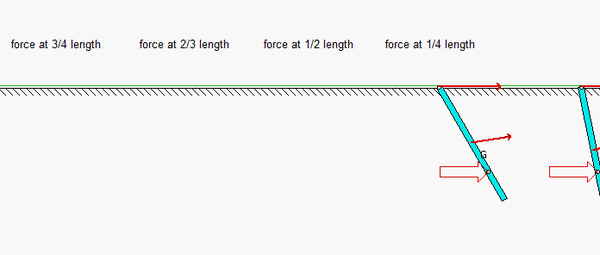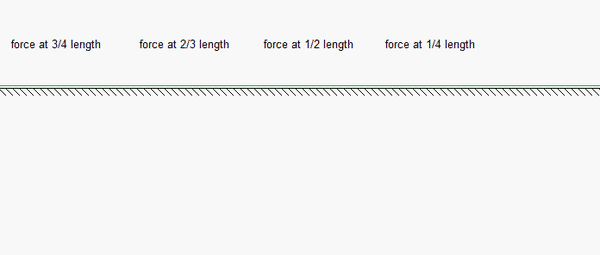
A thin, homogeneous bar of length L is support by a smooth sliding joint at the top end A. With the bar initially at rest, a force F is applied a distance of d below A. What is the instantaneous acceleration of end A as a result of the applied force?
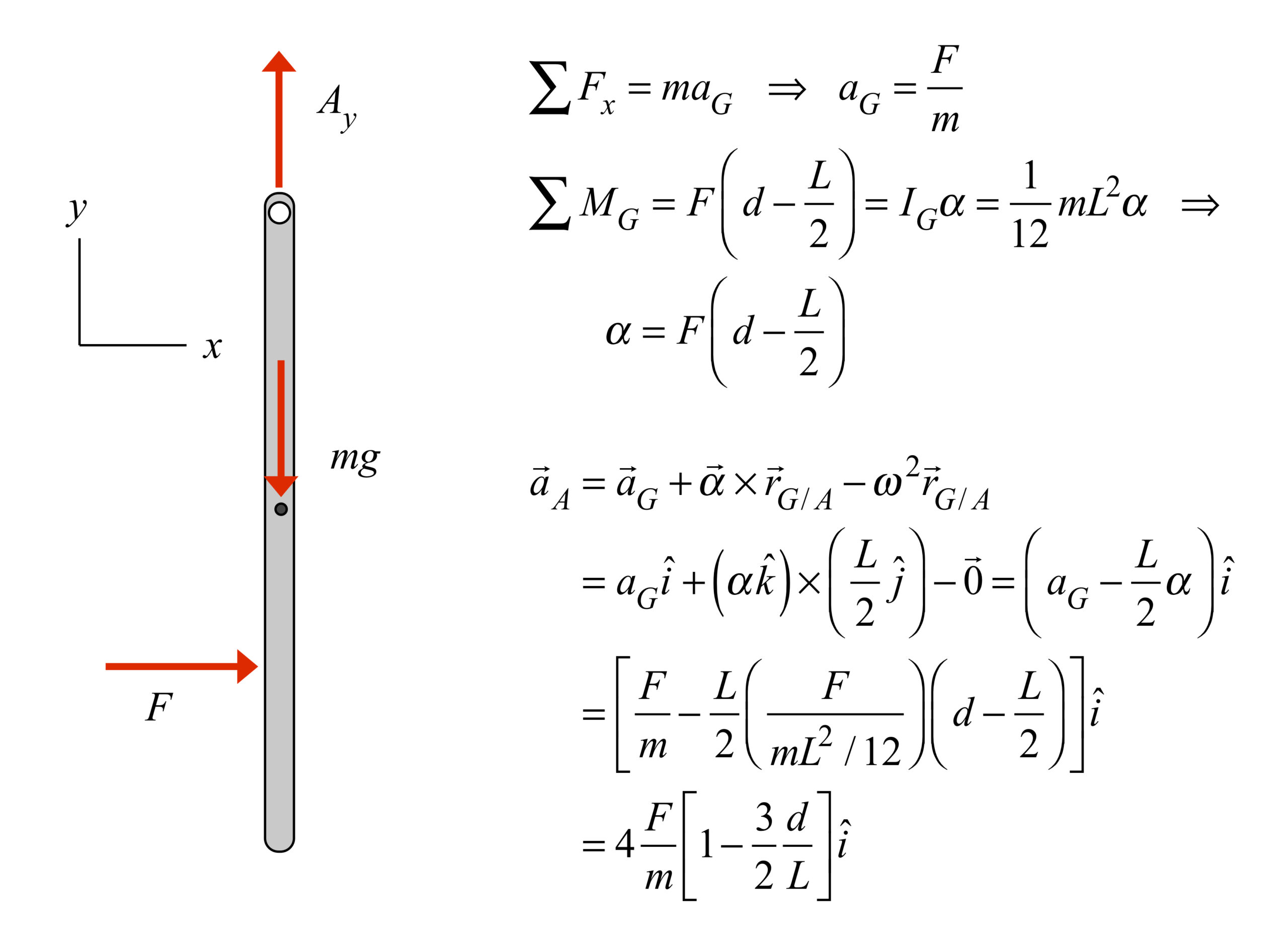
From the above, we see that:
- When d/L = 1/2 (force applied at the center of mass G), the acceleration of A is aA = F/m. This is expected since in this case the bar is in pure translation.
- When d/L = 2/3, the acceleration of A is aA = 0. The location of the applied force in this case is known as the "center of percussion" (or, "sweet spot"); that is, no force is required at end A in order to keep A stationary at the instant that the force is applied.
An animation of the simulation for this problem is shown for four values of the application point d. For d/L > 2/3, the acceleration of end A is initially to the left for a force applied to the right on the bar.