| Problem statement Solution video |
DISCUSSION THREAD
Discussion and hints:
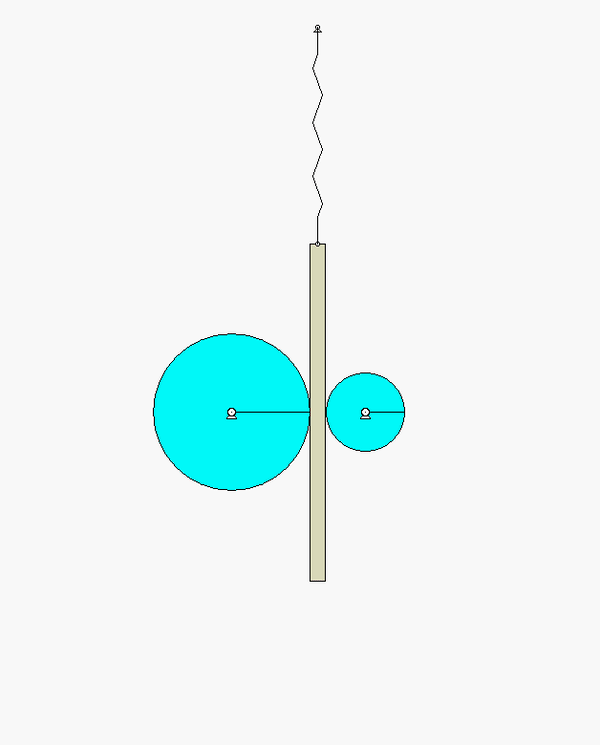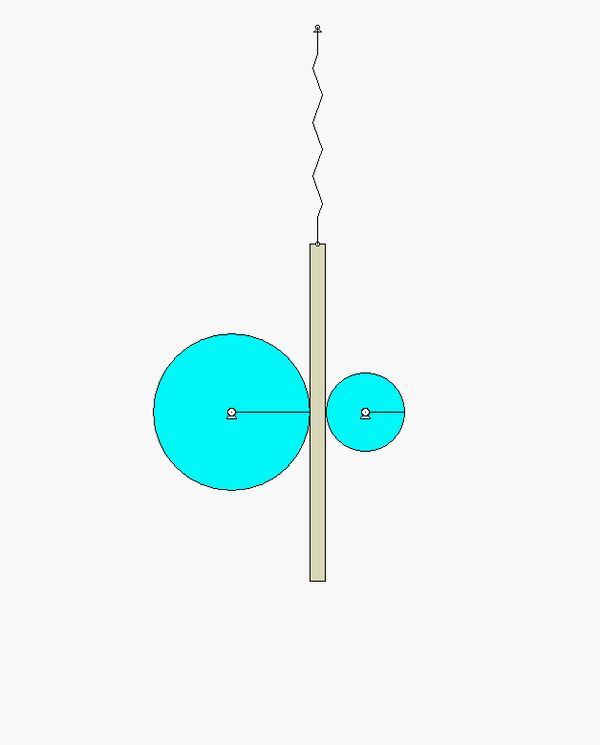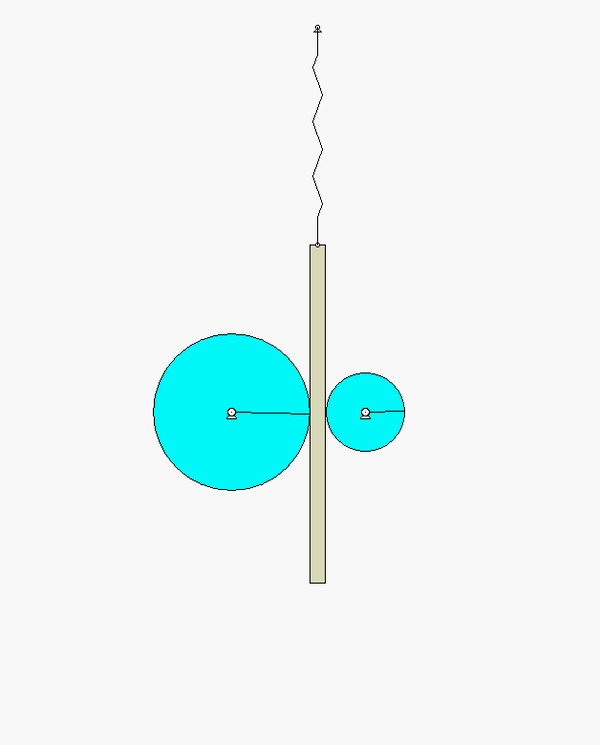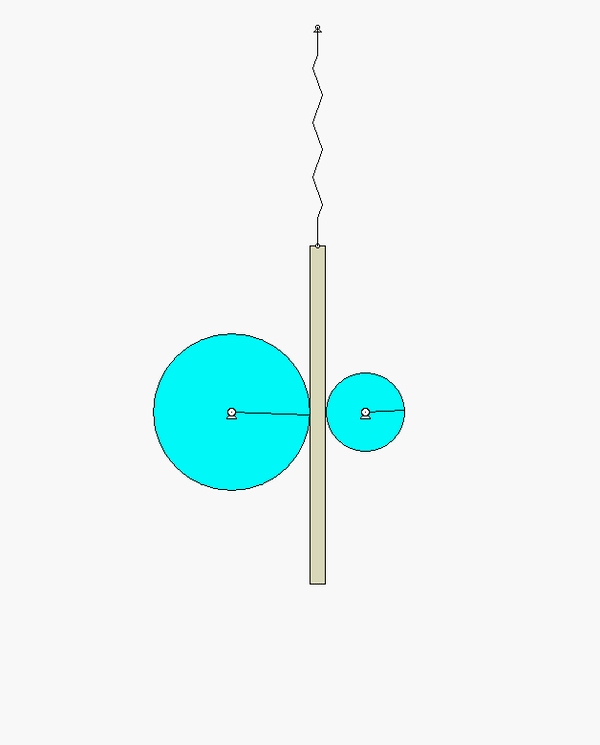
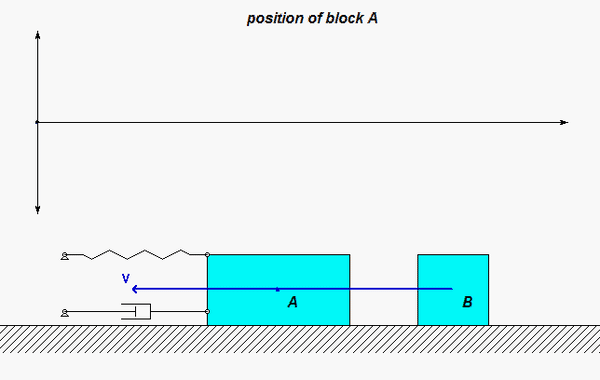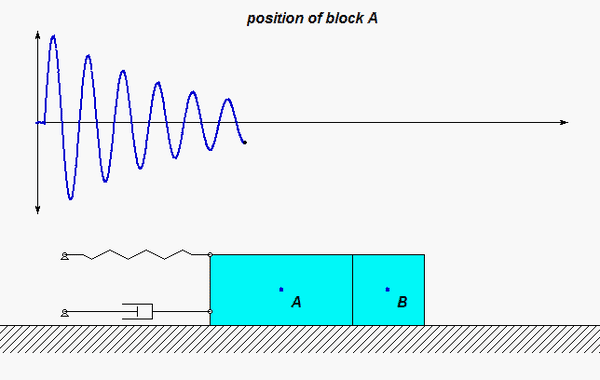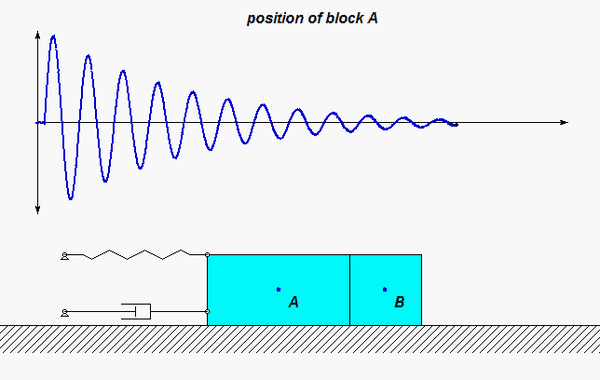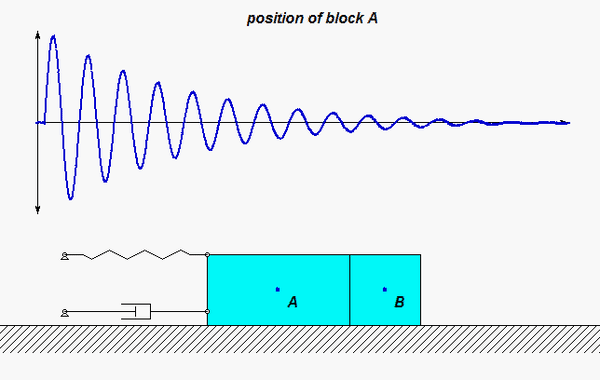
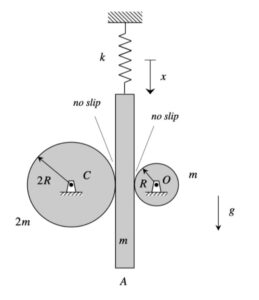
The derivation of the dynamical equation of motion (EOM) for a system is a straight-forward application of what we have learned from Chapter 5 in using the Newton-Euler equations. The goal in deriving the EOM is to end up with a single differential equation in terms of a single dependent variable that describes the motion of the system. Here in this problem, we want our EOM to be in terms of x(t).
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
Draw individual free body diagrams for the two disks and block A.
Step 2: Kinetics (Newton/Euler)
Write down the Newton/Euler equations for the two disks and block based on your FBDs above.
Step 3: Kinematics
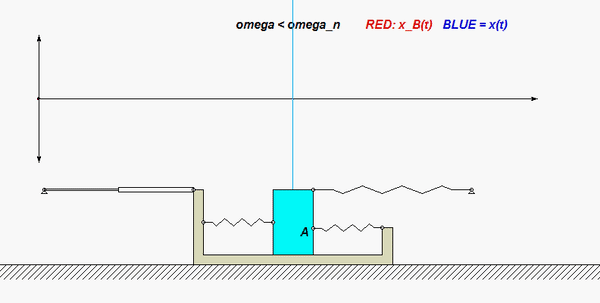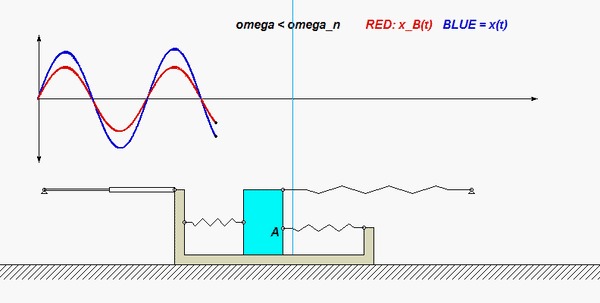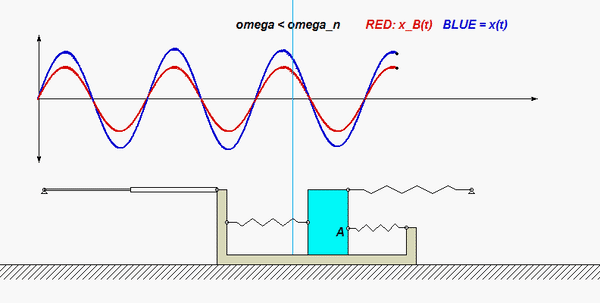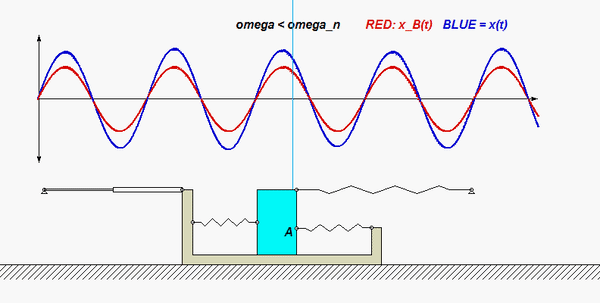
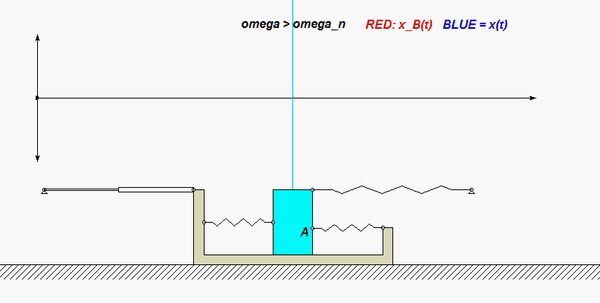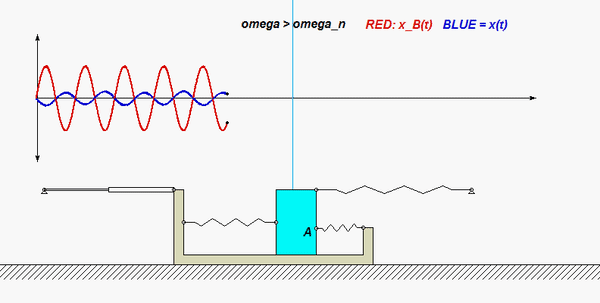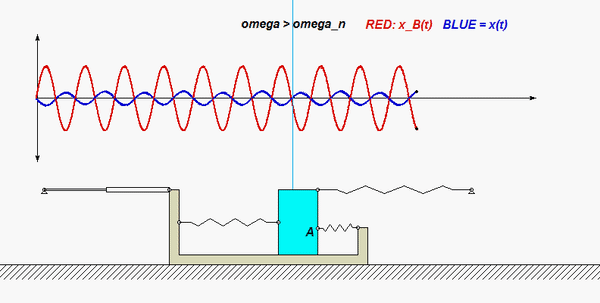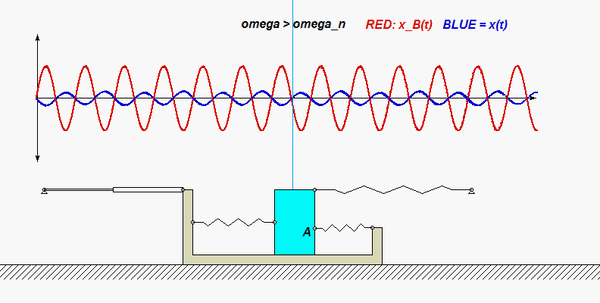
Use the no-slip condition between each disk and the block to relate the angular accelerations of the disks to the acceleration of the block. As confirmed by the animation above, the angular rotations of the disks are NOT the same, in either magnitude or direction.
Step 4: EOM
Combine your Newton/Euler equations along with your kinematics to arrive at a single differential equation in terms of the dependent variable x.
Any questions?