QUESTION:
If the angular velocity of a link in a mechanism is zero, does this imply that the angular acceleration of that link is also zero?
The short answer to that question is NO. If ω(t) represents the angular speed of the link, then the angular speed at some time "t" is the FUNCTION value of ω(t). On the other hand, the angular acceleration α(t) is the TIME DERIVATIVE of ω(t): α(t) = dω(t)/dt. Visually, if you make a plot of ω(t) vs. t, then α(t) is the SLOPE of the function ω(t). For a general function ω(t), there is no expectation that a zero value for ω(t) will correspond to zero value of α(t).
Consider the mechanism shown below, where link AB is rotating in the counter clockwise sense with a constant angular speed of ωAB.
An animation of this motion is shown below. Plots for the angular velocity and angular acceleration of link BC, ωBC and αBC, are provided in this animation.
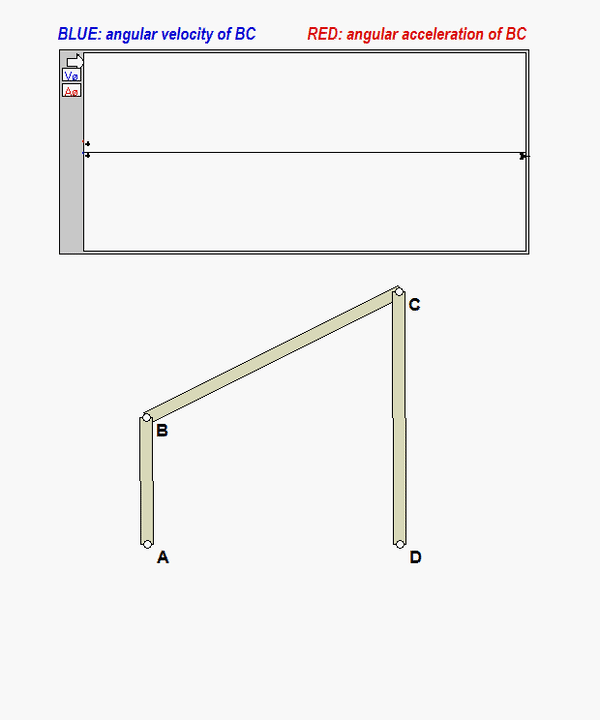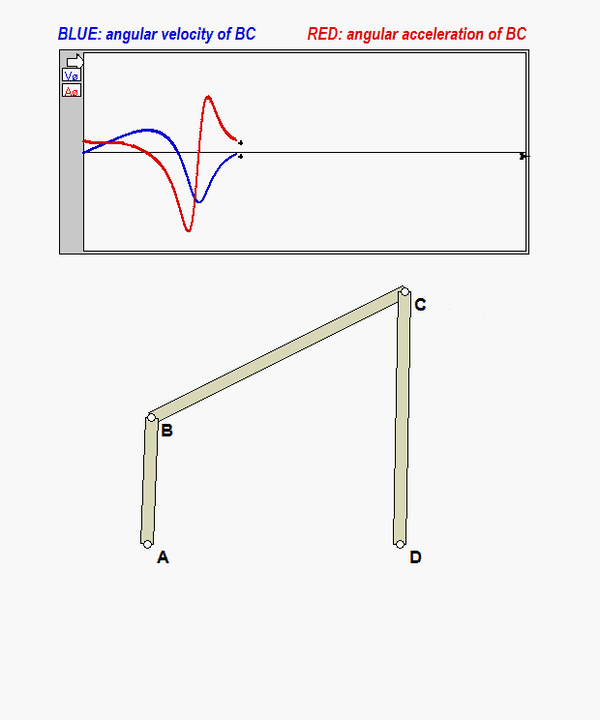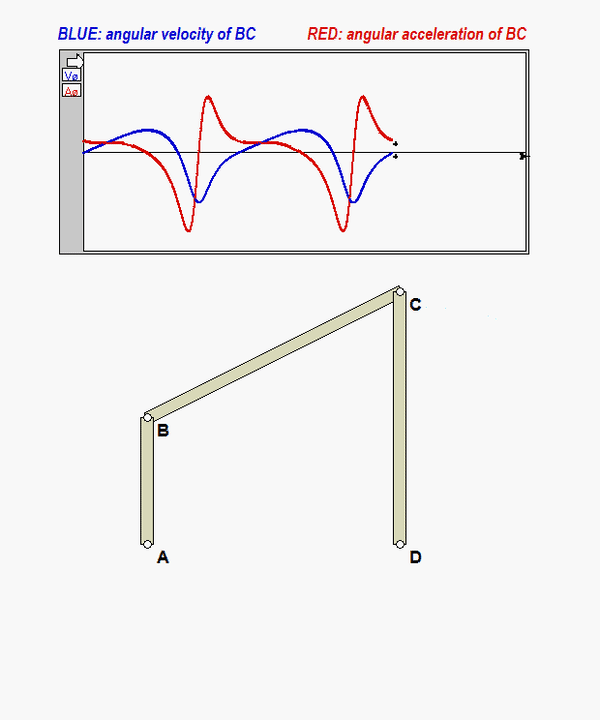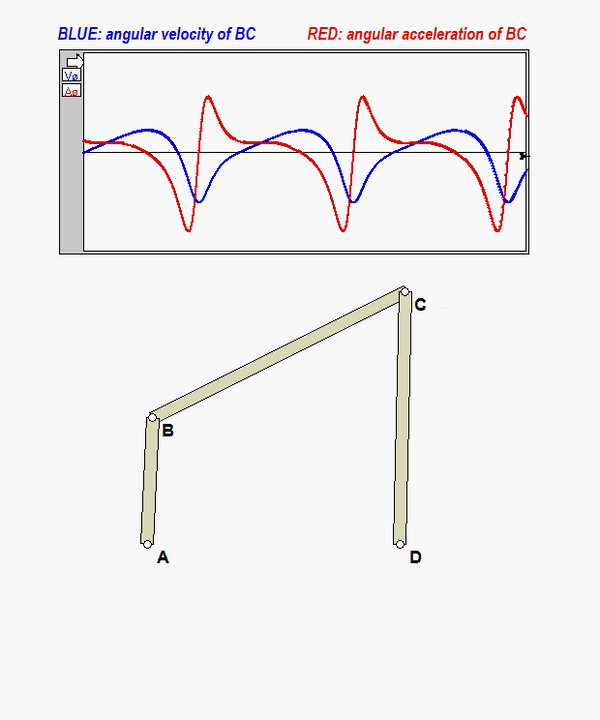
DISCUSSION
- Can you see from these simulation results that the red trace is the derivative of the blued trace?
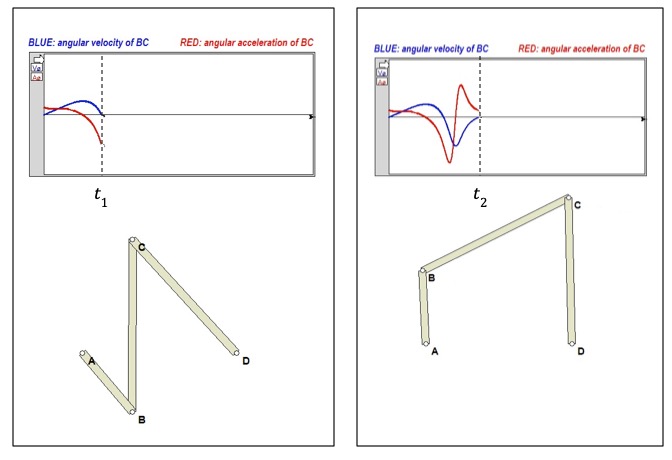
- Consider two discrete times t1 and t2 on these traces shown in freeze-frames of the motion below.
- At t1, the angular velocity is zero, with a non-zero (negative) angular acceleration. At that time, the direction of rotation for BC is changing from CCW to CW.
- At t2, the angular velocity is zero, with a non-zero (positive) angular acceleration. At that time, the direction of rotation for BC is changing from CW to CCW.
In summary, you should never assume that a zero value for angular velocity of a link means a zero value for angular acceleration of that link.