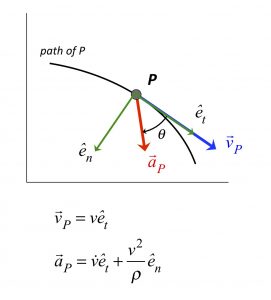
As we have seen in class, the velocity of a point P moving through space is always TANGENT to the path of P. On the other hand, the acceleration of P has BOTH normal and tangential components:
The tangental component of acceleration is the "rate of change of speed":
-
-
- If the speed of P is INCREASING, then the angle theta is less than 90 degrees.
- If the speed of P is CONSTANT, then the angle theta is equal to 90 degrees.
- If the speed of P is DECREASING, then the angle theta is greater than 90 degrees.
-
The normal component of acceleration is known as the "centripetal" component. It is proportional to the square of the speed, and inversely proportional to the radius of curvature of the path. The centripetal component of acceleration ALWAYS points toward the insider of the curved path. The normal component of acceleration for a straight path is ZERO - why??
Watch the animations below. On the left side, P is traveling with a constant speed; as discussed above, there is a 90 degree angle between velocity and acceleration. On the right side, P moves with increasing/decreasing speed. When the speed is increasing, the angle between v and a is less than 90 degrees, and greater than 90 degrees with the speed is decreasing.
