| Problem statement Solution video |
Note: Due to the weather-related changes in the course this week, the submission of this problem can be delayed until 11:59PM on Friday, January 30.
DISCUSSION THREAD
We encourage you to interact with your colleagues here in conversations about this homework problem.
Discussion and hints:

Enlarged view
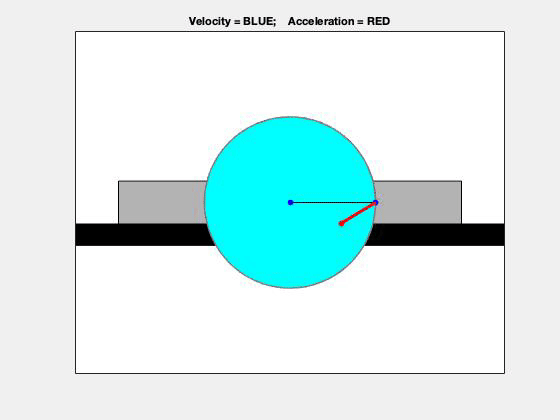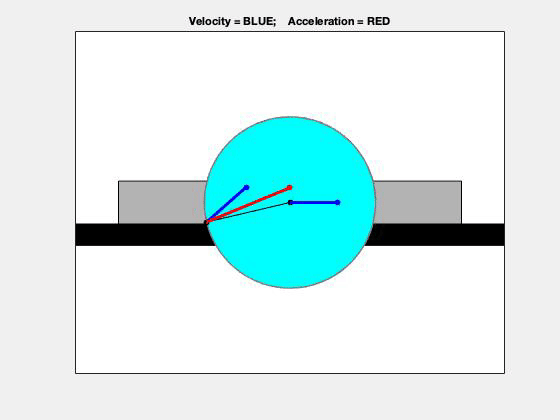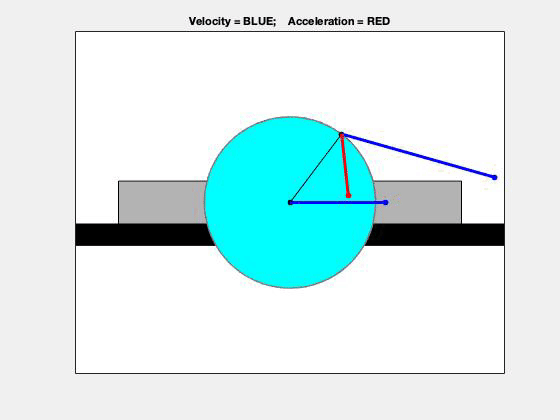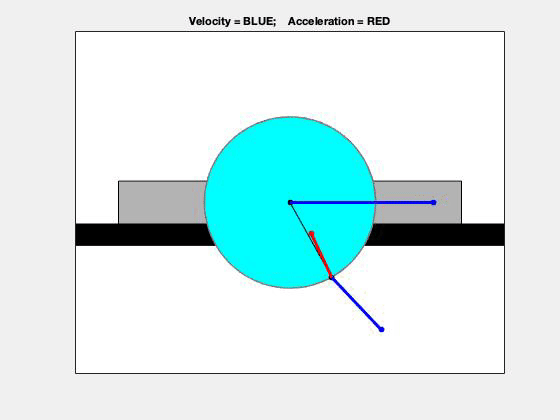
This problem is a straight-forward application of the planar rigid body kinematics equations. The velocity and acceleration of the center of the disk are known, as well as the angular velocity and angular acceleration of this disk. To find the velocity and acceleration of point A on the disk, you can use the following:
v_A = v_O + omega x r_A/O
a_A = a_O + alpha x r_A/O – omega^2*r_A/O
Using the enlarged view above, we can see the interplay between velocity (blue) and acceleration (red) of point A. Using what we learned back in Chapter 1, can you identify times when the speed of A is increasing and when it is decreasing? (Hint: Look at the angle between the velocity and acceleration vectors.) Using the top view, we can see the path of point A – is that the path that you expected for A?
Would it be correct to assume this problem only concerns the i and j directions since A and O are on the same plane? Do omega and alpha introduce the k direction?
Yes, all translational motion is in the xy-plane. The rotation of the disk is about the z-axis.
I am getting a velocity of 0 m/s but I think that’s wrong. I used the same equation as in the hint and got 3i_hat and -4*Ri_hat after solving it. Since R is 3/4, it’s just 3i_hat – 3i_hat. The acceleration I calculated has both i and j components, so shouldn’t the velocity also have some component in it?
I believe velocity shouldn’t be 0 m/s. I had a nonzero value. The fix could be that the omega value actually introduces the k_hat component, and when you solve with the appropriate equation provided above you won’t result in a zero value. Is this right?
Not necessarily; getting a velocity of 0 just means that the translational velocity component is 0. The non-zero acceleration comes from the rotational velocity component.
Hmm, I am coming to the same conclusion as Sanchika above. When I calculated the velocity using the given equations I got a result of 0m/s. However, when I computed the acceleration vector, I also had both i and j components. I saw Bobby’s message as well, and used the k_hat component when computing the cross product of angular velocity and vector r_A/O. This method resulted in the zero answer.
While I am not fully sure if this answer is correct (the visual representation provided above still seems to show a velocity at point A), one mistake that could have led others to an incorrect answer is forgetting to assign a negative sign to both the angular velocity and acceleration because they are working in the clockwise direction.
Are we assuming counter clockwise as negative omega and alpha? Definitely changes the final answer.
That depends on how YOU define your coordinate axes.
* If you define x as being positive to the right and y as being positive up, then by the right hand rule k_hat = i_hat x j_hat points OUTWARD from the page. In that case, CCW is positive and CW is negative.
* If you use different orientations for positive x and positive y, then you can end up with different results for the signs of CCW and CW.
Always use the right-hand rule to check out your signs.
First, the numbers provided in the homework problems change from semester to semester when that problem is used. The animations are based on simulations that were run for parameters that may or may not be the same parameter values for this semester. In short, the animations are to be used to provide a general understanding of the motion, not for detailed specifics for the numbers this semester.
Let’s reason through whether the velocity of A is zero for the parameters used this semester. From the kinematics equations, we know that the velocity of A is made up from the sum of two components:
* the velocity of O which is +3*i_hat
* the value of -omega*r*i_hat = -(4)*(0.75)*i_hat = -3*i_hat
The sum of these two terms is zero.
Make sense?
This may be a dumb question, but why wouldn’t R be -0.75 m in the J direction if A is located directly below the center of the circle?
Is there anyway to know the exact direction of acceleration for point A? To my knowledge we are supposed to intuitively know so we can solve the equation with coefficient balancing.
Velocity can be more easily verified than acceleration since there are only two terms in the equation. With acceleration having three terms, it is more challenging to visualize the results.
Please note that this problem is not one that requires coefficient balancing. You simply need to do the vector operations that are required on the right hand side of the equation in order to find the answer.
I am just a bit confused on the direction of each component. I believe the angular velocity and acceleration are k, v_o and a_o are i, but then R I’m not sure about. Because I can’t figure out how to get a j component in acceleration.
For the position of interest when A is directly below O, the position vector r_A/O is given by: r_A/O = -R*j_hat.
Using this in the rigid body acceleration equation referenced to point O, you will find that A will have a j_hat component.
I see, I was misunderstanding that vector thank you!