Homework H1.J – Sp 26

9 Comments
Problem statement
Solution video

DISCUSSION THREAD

Discussion and hints:

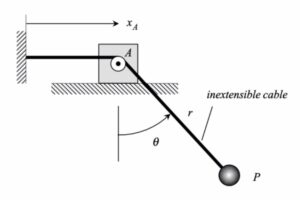
An observer riding along on block A will describe the motion of P relative to themself in terms of the radial distance r and the cable angle θ. Because of this, it is convenient to use the relative motion kinematics equations to write down the velocity and acceleration of particle P:  vP = vA + vP/A and aP = aA + aP/A , where the relative velocity and relative acceleration terms are written in polar form:

vP/A = r_dot er + r*theta_dot eθ

aP/A = (r_ddot -r*theta_dot2) er + (r*theta_ddot + 2r_dot*theta_dot) eθ

You will need to write the polar unit vectors er and eθ in terms of the Cartesian unit vectors, i and j, at some point before you can add together terms.

QUESTION: What is the relationship between xA and r? (Recall that the cable remains taut at all times.)

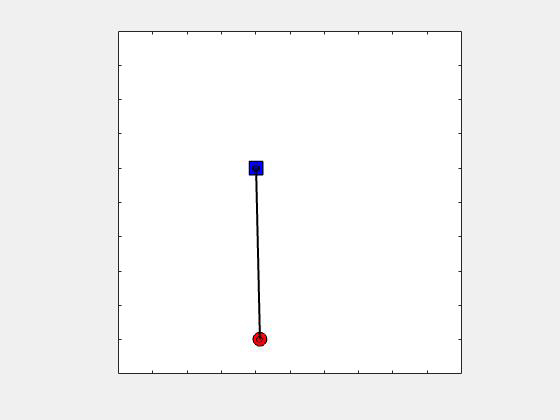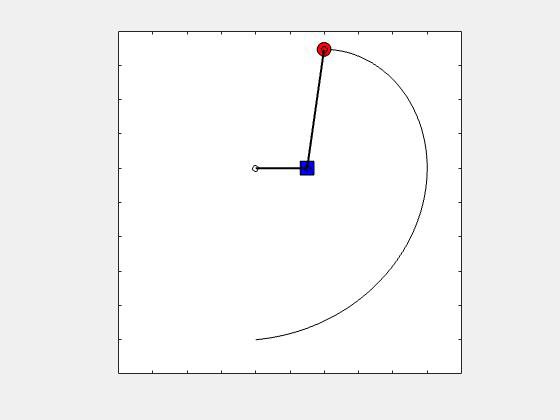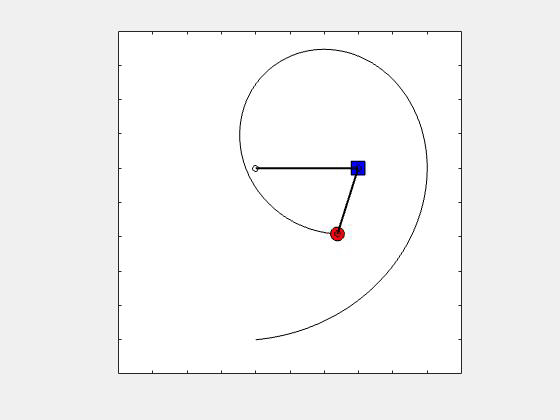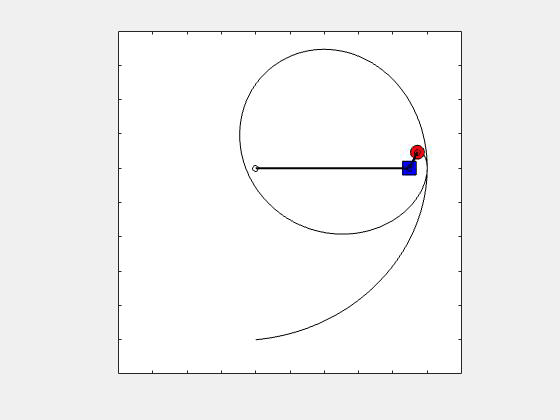
An animation showing the path of point P corresponding to θ_dot = constant is provided below. How does this true path differ from the view of the path as seen by the observer on A? Can you visualize that? HINT: The path seen by the observer on A is an inward spiral centered on the observer (point A).

Any questions??

9 thoughts on “Homework H1.J – Sp 26”

  1. For problem H1.J, I got a_A to be 0, since it is the time derivative of the constant velocity xdot_A. Does this sound right? Also, how do we know to apply relative kinematics here and how to identify what kinds of problems to apply this technique on?

    1. You are correct. Since block A is moving with a constant speed along a straight-line path, the acceleration of A is zero.

      The relative motion kinematics equations are useful for problems for which the path of the point as seen by a stationary observer is complicated and when the observed motion of the point by a moving observer is simplified. For this problem, the observer attached to A sees an inwardly-spiraling path. A stationary observer sees a path that is even move complicated. Good question!

      1

  2. To find values for r_dot and r_ddot, does the angle factor in for the derivatives of the cable length, or does the length of the cable only equal L = x_A + r?

  3. When asked about the viewpoint of the observer from point A, is it stating that the particle P itself will appear closer to the subject due to the movement from point A, or stating that the range of the object will appear smaller as the rotation progresses? How does that relate to the velocity and acceleration of point P?

    1. When asking about the viewpoint of the observer, we are talking about two things: the distance between P and A, and the angle through which P appears to rotate relate to the observer. That is, we are asking about r and theta.

      Use the polar kinematics description to write down the velocity and acceleration of P as seen by the observer in terms of r, r_dot, r_ddot, theta, theta_dot and theta_ddot.

      Does this help?

      1

    1. The relative motion equation goes as:

      v_P = v_A + v_P/A

      Since A moves only in the direction of the horizontal surface shown, A has only an i_hat component (assuming that you align the x-axis with that horizontal surface. From this, you see that v_A adds on only a component in the i_hat direction.

Leave a Reply