Ask and answer questions here. Either way, you will learn.

---

DISCUSSION and HINTS
In this problem, we desire to relate the rotation rates of link OA and the disk.

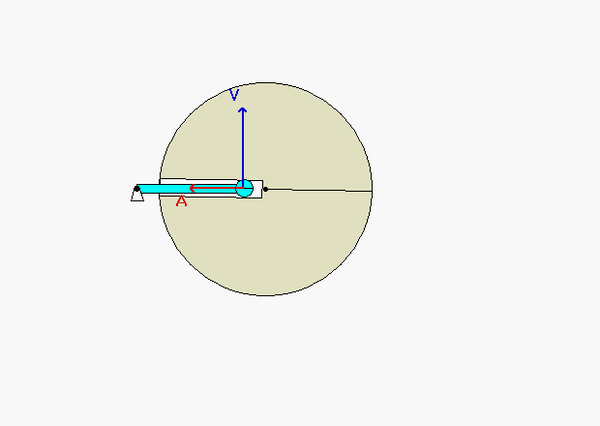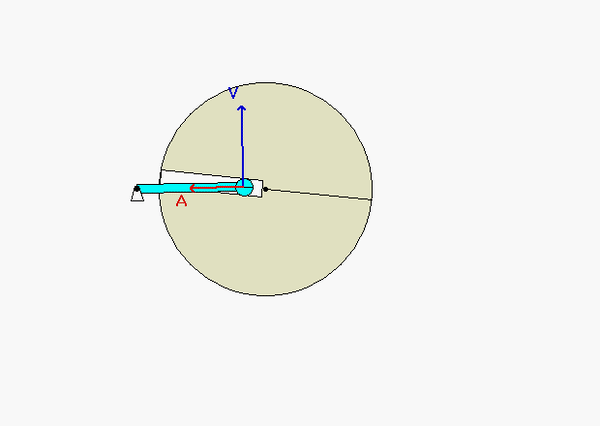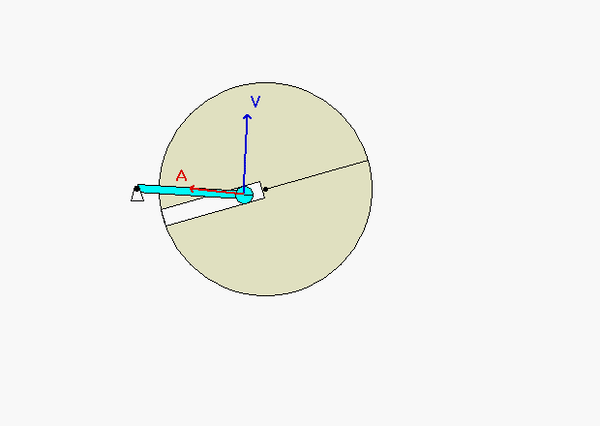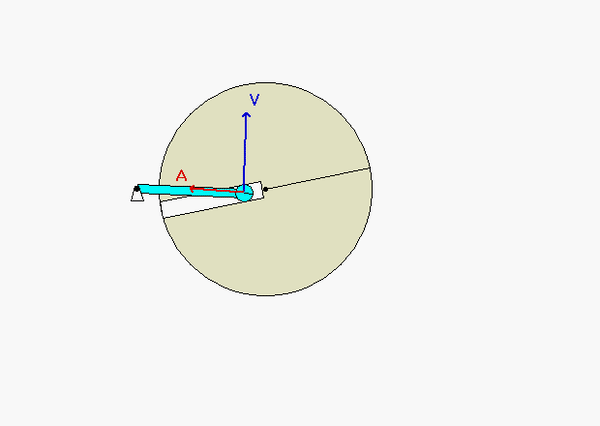
With the two rigid bodies connected by a pin-in-slot joint, we are not able to use the previous rigid body kinematics equations by themselves. Let’s discuss that below.

Velocity analysis
Here, we can use the rigid body velocity equation to relate the motions of O and A:

v_A = v_O + ω_OA x r_A/O

However, we cannot use a rigid body velocity equation to relate the motion of points A and B (the reason for this is that A and B are not connected by a rigid body). In its place, we can use the moving reference frame velocity equation with an observer attached to the disk:

v_A = v_B + (v_A/B)_rel + ω x r_A/B

where ω is the angular velocity of the observer, and (v_A/B)_rel  is the velocity of A as seen by our observer on the disk. Note that with the observer being attached to the disk, this observer sees motion of A only along the slot.

Combine these two equations to produce two scalar equations.

Acceleration analysis
We will use the same procedure for acceleration as we did for velocity – use a rigid body equation for OA and a moving reference frame equation relating A and B.

a_A = a_O + α_AOx r_A/O + ω_AO x (ω_AO x r_A/O)
a_A = a_B + (a_A/B)_rel + α x r_A/B + 2ω x (v_A/B)_rel + ω x (ω x r_A/B)

where α is the angular acceleration of the observer, and (a_A/B)_rel  is the acceleration of A as seen by our observer on the disk. Again, note that with the observer being attached to the disk, this observer sees motion of A only along the slot.

Combine these two equations to produce two scalar equations.