Discussion
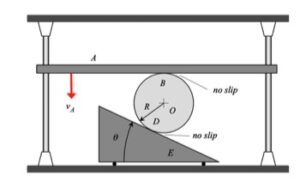
Consider the motion of the system shown below,
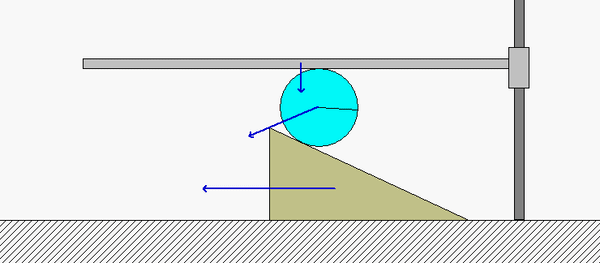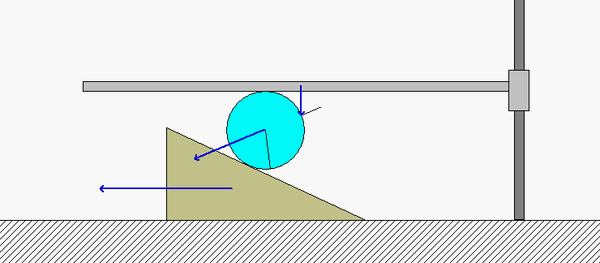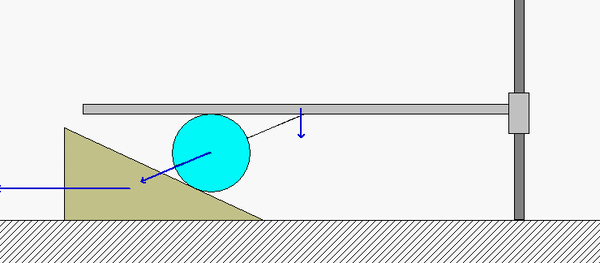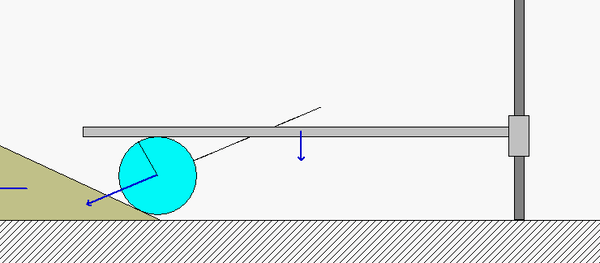
along with a freeze-frame of this motion that follows:

Points B and D on the disk roll without slipping on the horizontal guide A and the wedge E, respectively. Because of this:
- B has a velocity vB which points straight down, with the same speed vA as the horizontal guide A.
- D has a velocity vD which points directly to the left with the same speed as the wedge E.
The instant center (IC) of the disk (call it point C) therefore exists at the intersection of the perpendiculars to vB and vD. Note that point B is much closer to the IC than point D. What does this say about the relative sizes of vD and vB? Is this consistent with the speeds of D and B shown in the above animation?
HINTS:
- Use the above discussion points to locate the IC for the disk.
- Determine the angular speed of the disk based on the speed of B and the distance from B to C.
- The speed of the wedge E is found by using the angular speed from above and the distance from C to D.
Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.