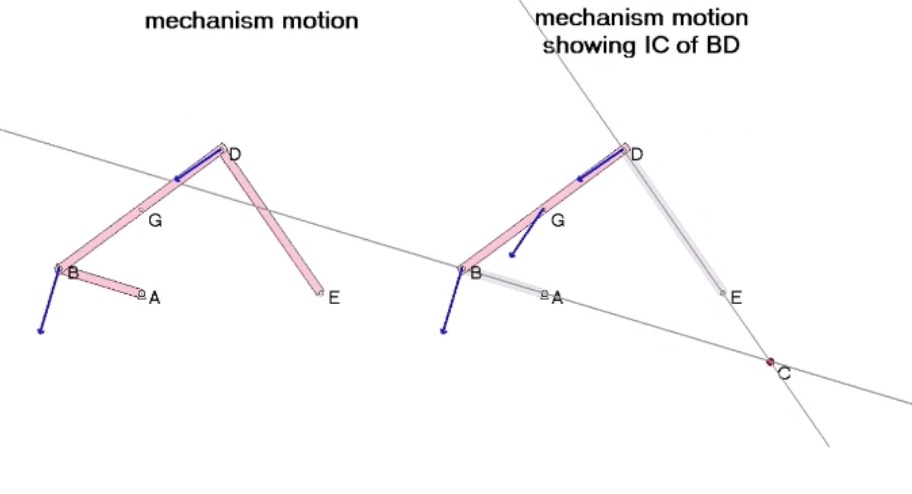
Consider the mechanism shown below made up of moveable links AB, BD and DE. Link AB is rotating CCW at a constant rate. Point C is the center of rotation for BD, where point C is at the intersection of perpendiculars to the velocities of points B and D. Therefore, the velocity of any point on BD is perpendicular to the line connecting that point with C, and the speed of that point is proportional to the distance of that point from C. Since the location of the rotation center C moves with the mechanism motion, it is known as the “instant center” of rotation for BD. You can observe this in the video shown below.

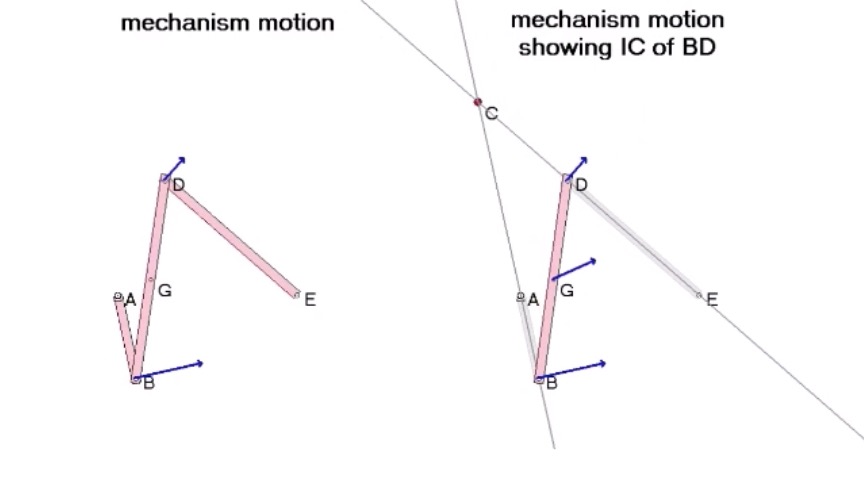
Watch the velocity of point G on link BD. The direction of this velocity is perpendicular to the line connecting G and C. This is true because at that instant, BD is rotating about the instant center C.

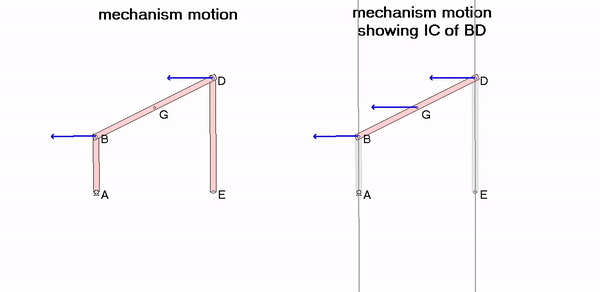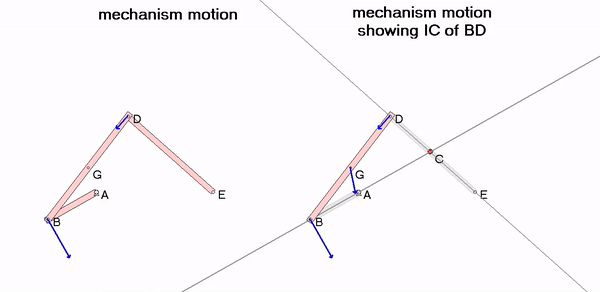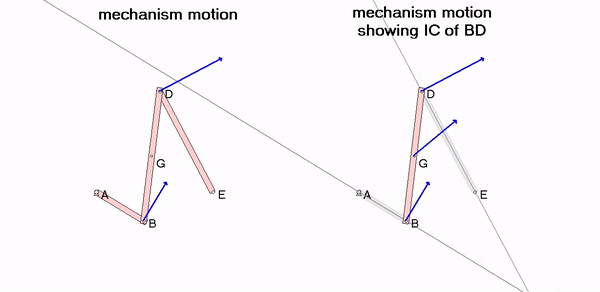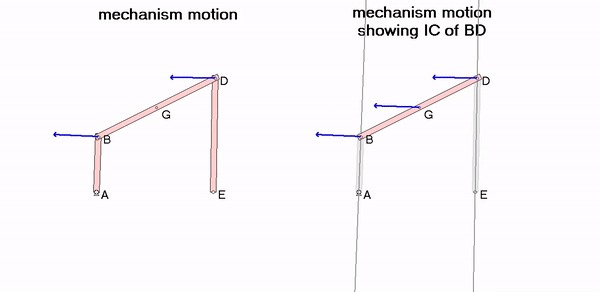
When link AB and DE are parallel (positions for which the instant center C is at ∞), the angular velocity of BD is zero – can you see this in the animation? Shown below are two freeze-frames, one with the IC for BD below E and one with the IC for BD above  D. In each freeze-frame, can you see that the direction of velocities for all points on BD are perpendicular to a line connecting that point to the IC (point C)?