Ask and answer questions here. Help others with thoughtful responses to their questions. You will learn from the experience.

---

DISCUSSION and HINTS
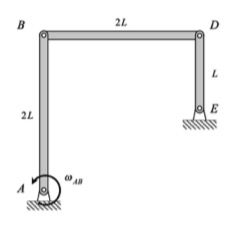
This mechanism is made up of three links: AB, BD and DE. You are given the rotation rate of link AB, and are asked to find the angular velocities and angular accelerations of links BD and DE. At the position shown, it is known that ω_AB = constant.

From the animation below, we are reminded that B and D move on circular arc paths with centers at A and E, respectively. The velocities of B and D are always perpendicular to the lines connecting the points back to the centers of the paths. Can you visualize the location of the instant center (IC) of link BD as you watch this animation? For the position of interest in this problem, you see in the animation that the velocities for all points on BD are the same – is this consistent with the location of the IC for BD at that position?

Velocity analysis
Where is the instant center of link BD? What does this location say about the angular velocity of BD?

Acceleration analysis
Write a rigid body acceleration equation for each of the three links in the mechanism:

a_B = a_A + α_AB x r_B/A – ω_AB²r_B/A
a_D = a_E + α_DE x r_D/E – ω_DE²r_D/E
a_B = a_D + α_BD x r_B/D – ω_BD²r_B/D

Combining together these three vector equations in a single vector equation will produce two scalar equations in terms of α_BD and α_DE.