Discussion and hints:
For this problem, the “Given” information is in terms of the path kinematical description. The “Find” asks for parameters that are part of the polar kinematical description.
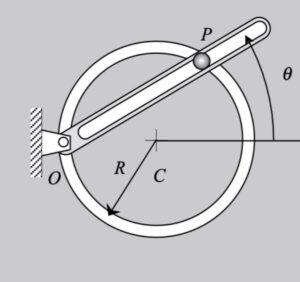
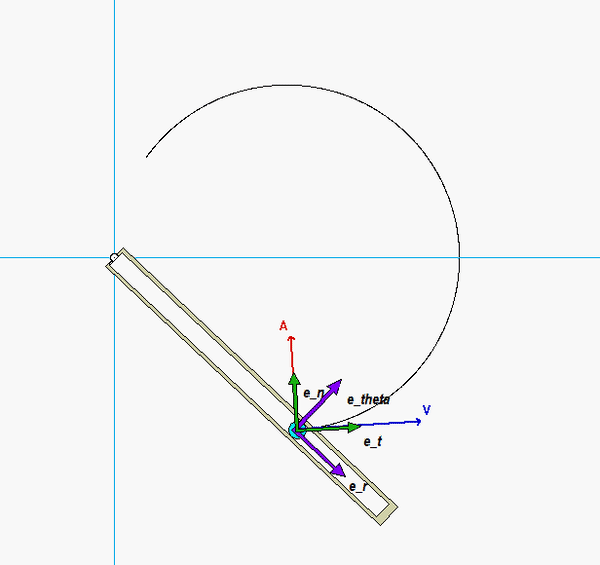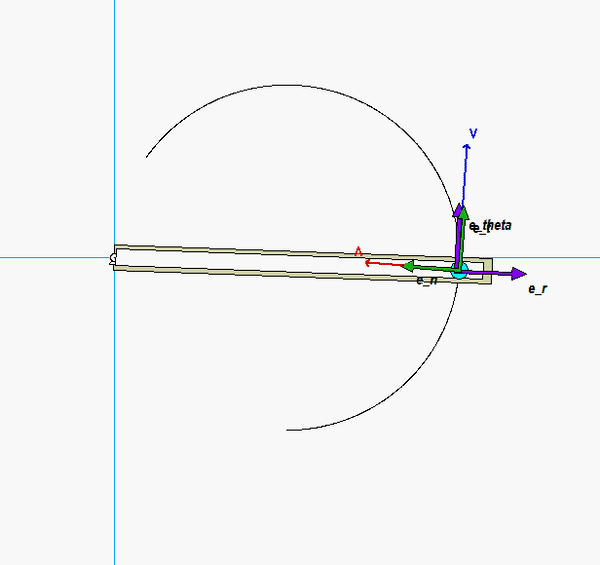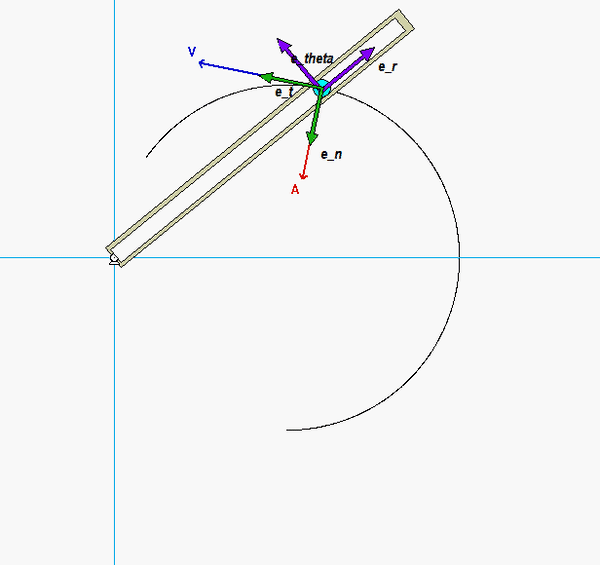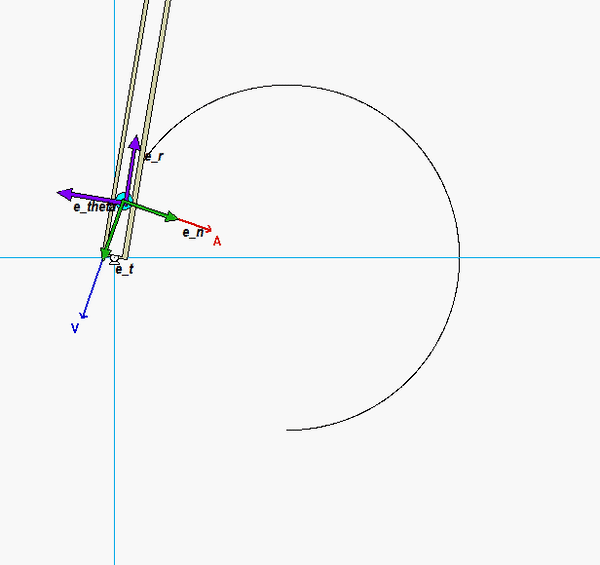
The key to the solution of this problem is being able to correctly draw the sets of path and polar unit vectors.
- The path unit vectors et and en are tangent and perpendicular to the circular slot (the path).
- The polar unit vectors are defined as: er points outward from O to P (along the slot in the arm), and eθ in the direction perpendicular to er (perpendicular to the slot) and in direction of increasing angle θ (counterclockwise rotation from er).
For the position of interest (θ = 45°), these vectors are as shown below.
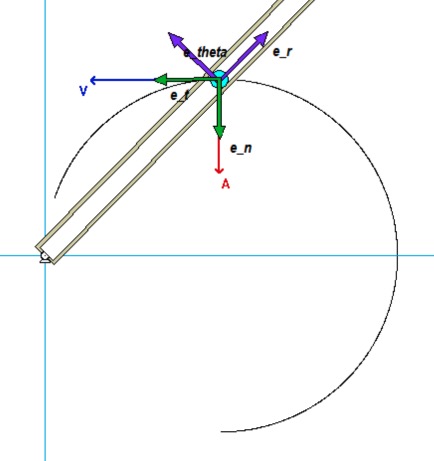
It is recommended that you write the polar unit vectors in terms of the path unit vectors, use projections of v and a onto the polar unit vectors to produce four equations for the four unknowns. (There are a number of equivalent ways to solve this problem involving either vector projections or balancing of coefficients in the kinematics equations, as detailed in lecture and in the lecture book.)
Warning: Do not confuse the roles played by “r” and “R” in this problem.
The animation below shows the results of this analysis over a range of angles θ. There is an interesting result here. These results show that the acceleration vector is always perpendicular to the path (the circular slot). This is rarely the case. What is special about this problem that makes it true here? HINT: Think about the relationship between the angle of rotation of the arm and the angular rotation of P around the circle.
Any questions??