
We encourage you to interact with your colleagues here on conversations about this homework problem.
With the polar description, we write the velocity and acceleration vectors for a point in terms of the polar unit vectors er and eθ. These two unit vectors are shown in magenta in the animated GIF below.
- er points outward from the observer O toward point P
- eθ is perpendicular to er and points in the positive θ direction.
The velocity (in blue) is seen to be tangent to the path, as expected, The acceleration (in red) has both tangential and normal components: the normal component always points inward on the path, and the size and sign of the tangential component is directly tied to the rate of change of speed of P, also as expected.
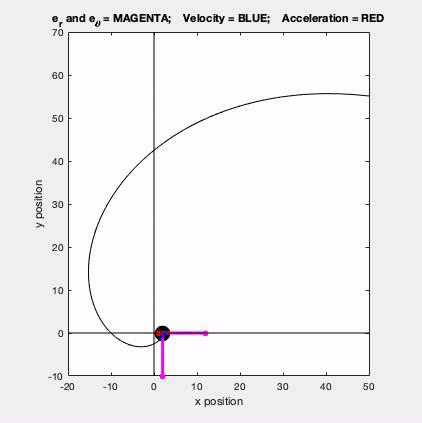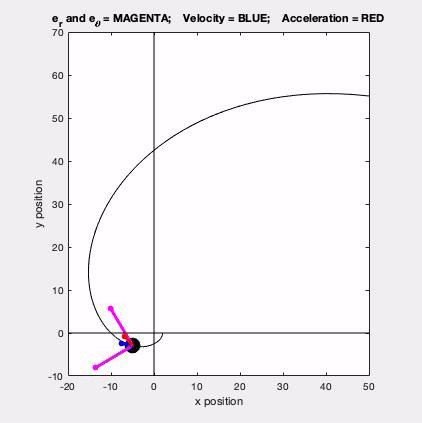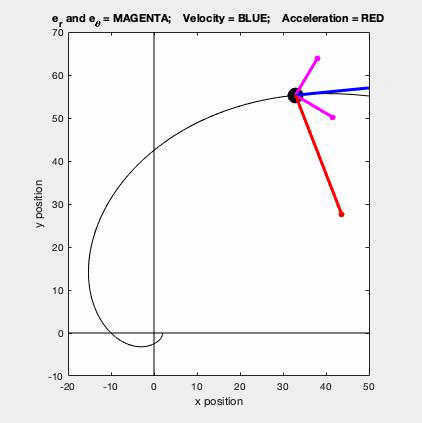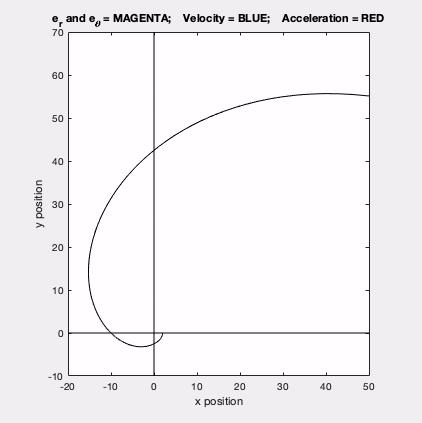
In terms of problem solving, this problem is straight forward. Both r and θ are given as functions of time. The components of the velocity and acceleration vectors are found directly from the differentiation of r and theta with respect to time. The chain rule of differentiation is NOT needed here.
Some additional observations:
- Although r_ddot = constant, the r-component of acceleration is NOT constant.
- Although θ_ddot = 0, the θ-component of acceleration is NOT zero.