Discussion and hints:
For this problem, the “Given” information is in terms of the Cartesian kinematical description. The “Find” asks for parameters that are part of the path kinematical description.
For the Given part of the kinematics, you will need to find the first and second derivatives of y with respect to time using implicit differentiation of the the path equation: xy = b, and using that the first time derivative of x is a constant value of c.
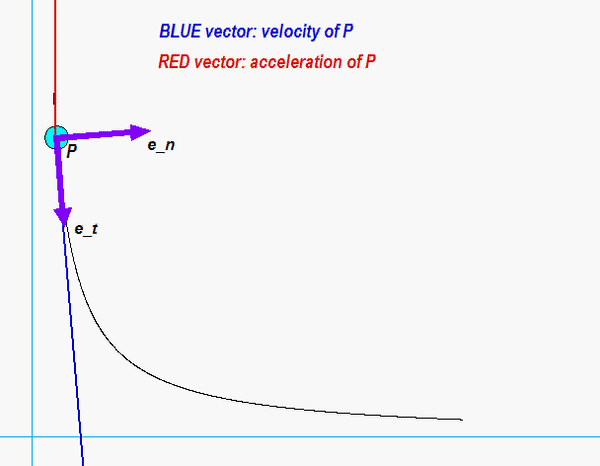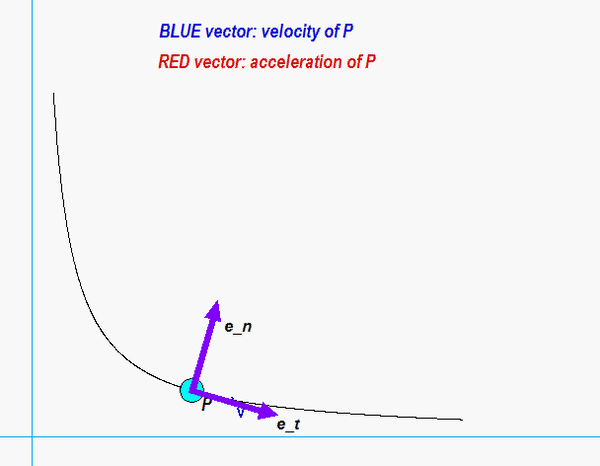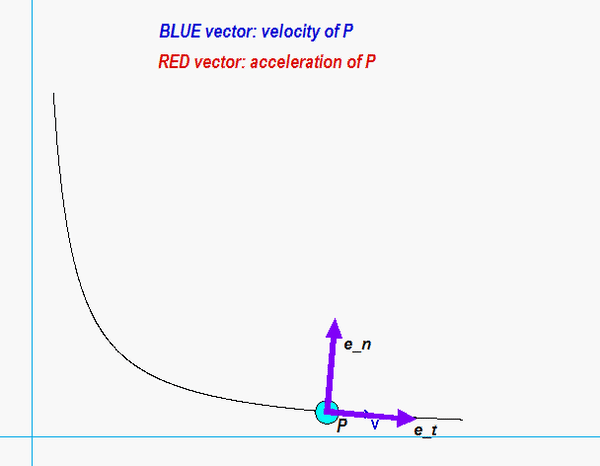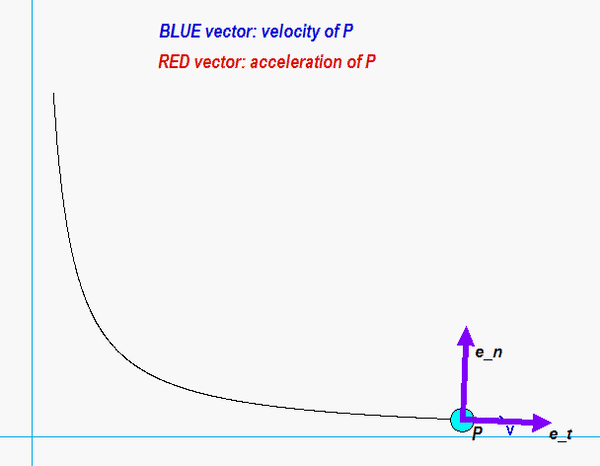
Next, you need to relate the Cartesian and path descriptions of the acceleration. There are many approaches in doing this. The most straight-forward approach is to use the projection of acceleration onto the unit tangent vector to find the rate of change of speed: v_dot = aP • et, where the unit tangent is found from et = vP/vP. The radius of curvature can then be found directly from the magnitude of acceleration equation: aP2 = v_dot2 + (vP2/ρ )2.
Recall that the sign of v_dot tells us whether P is increasing or decreasing in speed. From the animation below, we see that the acceleration vector has a negative et throughout the full range of motion. Alternately, you can say that the angle between velocity and acceleration is greater than 90° over that motion. So: increasing or decreasing in speed?
Any questions??